The influence of intraocular pressure on the damping of a coupled speaker–air–eye system

Although glaucoma is currently the world's most common cause of irreversible blindness, there is no curative therapy available to date. The major risk factor that can be influenced in order to stop disease progression is the eye pressure (IOP). Therefore early diagnosis of an altered IOP is essential for the goal of preserving vision. A novel IOP measurement principle for a handheld noncontact self-tonometer shall be validated.

The measurement principle uses a pressure pulse generated by a loudspeaker to cause vibrations of the eye. In order to reach the required sound pressure, a closed pressure chamber is placed on the human orbit. With a microphone and a displacement sensor the dynamic behavior of the entire system is detected. In this article the abovementioned principle is being analyzed on porcine eyes under laboratory conditions.

The combination of the loudspeaker, the pressure chamber, and the eye to be measured can be described as a coupled spring–mass–damper system. It is demonstrated for enucleated porcine eyes that a defined IOP variation leads to a change in the system's damping ratio. Considering only stochastic deviations, the derived standard uncertainty for the determination of the IOP amounts to < 1 mmHg in the physiological range.

The in vitro measurements on porcine eyes help the understanding of the underlying physics and demand for further research on the influence of biometric parameters on eye vibrations. However, the laboratory results provide the basis for a gentle noncontact tonometry method with great applicational prospects. Data is currently being collected on human subjects in a clinical trial, to corroborate the measurement principle in vivo.

1 Introduction

Glaucoma is currently the most common cause of irreversible blindness worldwide (Jonas et al., 2017). It comprises malfunctions in the eye that lead to a subsequent loss of neuronal retinal cells (Giaconi et al., 2016; Grehn, 2012; Yung et al., 2014). There is no curative therapy available to date which makes early detection and avoiding further damage the most effective medical intervention (Giaconi et al., 2016). Besides the subjective method of visual field testing, the correct measurement of the patient's intraocular pressure (IOP) constitutes a key factor for the diagnosis and follow-up treatment of glaucoma. Lowering the IOP is the main therapeutic approach, either through medication or surgery. Thus, a reliable measurement of the IOP represents the current key aspect to stop progression of glaucoma (Giaconi et al., 2016).

The Goldmann Applanation Tonometer (GAT), initially described in 1955 (Goldmann and Schmidt, 1957; Rosentreter et al., 2011), is still the clinical gold standard for IOP measurements and has an uncertainty of 1–2 mmHg (Cook et al., 2012), which can increase to 3.8 mmHg in interindividual comparison (Rosentreter et al., 2011). It detects the static force that is needed to indent the cornea with a glass stamp to a predefined flattened area with a diameter of 3.06 mm. The IOP can then be calculated according to the Imbert–Fick law (Goldmann and Schmidt, 1957; Rosentreter et al., 2011). Aside from the medical experience of the user (Rosentreter et al., 2011), the uncertainty of the result also depends on the thickness and age-related material parameter changes in the cornea (Tonnu et al., 2005). In addition, the measurement requires a local anesthetic, and the procedure is unpleasant, carries infection risks, and can only be performed by physicians and optometrists.

Noncontact tonometers, such as air-puff tonometers, reduce these negative factors to a certain extent (Giaconi et al., 2016). By using an air impulse, the elapsed time to flatten the cornea is measured, which defines the pressure that had to be applied. Despite its dynamic appearance, the method is based on the same static physical principle as the GAT (Giaconi et al., 2016). The results correlate well with GAT measurements in the physiologically desired IOP range from 10 to 20 mmHg (Giaconi et al., 2016). However, the measurement uncertainty of air-puff tonometers of 5 mmHg is larger than that of the GAT (Derka, 1980; Rosentreter et al., 2011). Besides the dominant use for out-patient screening tests, air-puff tonometers do not meet clinical requirements of an uncertainty of <3 mmHg and cannot be used in the home environment (Grigorian et al., 2015).

Several concepts exist that try to provide the potential of home measurements to yield diurnal IOP trends. The Ocuton S, which is based on the measurement principle of the GAT following the concept of Draeger (1993), leads to a deviation of 6 mmHg from the mean of GAT reference measurements (Yung et al., 2014). Yet the contact-related disadvantages of the GAT exist for the Ocuton S as well. With the pressure phosphene tonometer, an unpowered spring applanation tonometer that indents the eye through the eyelid, no anesthetic is required, but measurements reach an absolute mean difference from the GAT reference of 6.6 mmHg (Yung et al., 2014). The Tiolat iCare measurement device evaluates the bounce-back of a small plastic stick that is shot onto the cornea, and is therefore considered to use a dynamic principle. The iCare reaches a deviation of ±3 mmHg from the GAT measurements (Munkwitz et al., 2008). Although it is not considered a self-tonometer and generates higher deviations when it is not pointed directly on the vertex (Muttuvelu et al., 2012), it helps with the IOP measurement for children (Grigorian et al., 2015). Yung et al. (2014) conclude that there is no approved technology for measuring diurnal IOP trends in a home environment to date.

Instead of the static pressure estimation based on the Imbert–Fick law, dynamic approaches to noncontact tonometry try to analyze changes in mechanical eigenvalues due to different IOP levels of the eye. It was shown through finite-element analysis and optical measurements of the corneal vibration response of an acoustic excitation that the resonant frequencies of the eyeball change with the IOP (Drescher, 2000; Gundlach, 2003; Hey, 2003). Hey (2003) estimated a sensitivity of 3 Hz mmHg⁻¹ for one tested subject. Although the results seemed promising, there are no medical devices available based on this principle so far. Considering the measurement uncertainty of air-puff tonometers, no noncontact tonometers exist which meet the clinical requirements.

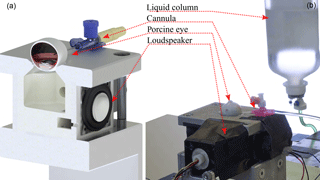
Figure 1 (a) Cross section of the measurement setup (CAD illustration) with the inside of the pressure chamber, a 30 mm loudspeaker, and a model of a porcine eye connected by a cannula. (b) Laboratory experiments with a freshly enucleated porcine eye and a liquid column for pressure application. The diaphragm movement of the loudspeaker is detected by an infrared reflection sensor represented by CNY70 in front of it.

A study by von Freyberg et al. (2009) presented a noncontact measurement approach that is based on the acoustic stimulation of the eye to be measured. The general distinction of IOP variations in a porcine eye regarding observed changes in the pressure attenuation in an enclosed chamber was demonstrated. However, a detailed characterization or a plausible physical model of the measurement concept was not provided. Therefore the potential of this measurement approach remains an open question.

For these reasons a dynamic IOP measurement system based on the approach described in von Freyberg et al. (2009) is presented and characterized with respect to the achievable measurement uncertainty. Note that the results derived from the experiments are necessary for the definition of the requirements for a discrete, handheld self-tonometer, which is the long-term aim of our research. The measurement system, which is formed by a loudspeaker, a pressure chamber, and the patient's eye, can be treated as a coupled spring–mass–damper system. The response of the mechanical system is measured by an optical displacement sensor in front of the loudspeaker's diaphragm, and a microphone in the pressure chamber. The presented work now provides a clear physical model of the measurement principle that explains the relation between IOP values and the damping ratio of the coupled mechanical system. Allocating the adjusted IOP values to the oscillation parameters of the system's response allows the calculation of the expected uncertainty for the IOP determination for the first time. The measurement principle and the experimental setup is described in Sect. 2. The IOP measurement system is characterized with experiments on porcine eyes, which is presented in Sect. 3. The discussion of measurement errors and a respective comparison with other measurement devices follows in Sect. 4. The article closes with a summary in Sect. 5.

2 Methods

2.1 Measurement principle

The principle of the IOP measurement approach can be illustrated with the behavior of a pressurized ball that is dropped from a specified height. The height of the ball bouncing back depends on its inner pressure as well as the material elasticity. The lower the pressure level is, the lower the bouncing height is, since more energy is consumed by deformation processes of the ball (Cross, 1999). This phenomenon is linked to the behavior of a damped harmonic oscillator where the amount of damping defines the ratio between consecutive peaks in a harmonic signal. It is postulated by the authors that the eyeball behaves accordingly. At low IOP levels the deformation of the cornea is assumed to be larger, since more work is expended on the eye. Work is defined as

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle }w=F\cdot s\end{array}$$

and is the product of a constant magnitude force F that is multiplied by a distance s in the direction of the force. The amount of work that is performed on the eye converts a measurable share of the inner energy of the system into heat. With a variation of the IOP the energy conversion in the pressure chamber changes, which is measurable as the damping of the characteristic oscillation of the system. This can be measured with a microphone that records the sound pressure level (SPL) within the pressure chamber and by a displacement sensor that detects the movement of the loudspeaker's diaphragm.

A general spring–mass–damper system is described by

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle }m\ddot{x}+d\dot{x}+kx=\mathrm{0},\end{array}$$

where m is the mass, d is the damping constant, and k is the spring rate (Niedrig and Sternberg, 2013). If the system is excited by an external force, the time it takes for the oscillation to settle down is defined by d. The fade-out of a technical harmonic oscillation against the time reads

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle }x\left(t\right)=x_{\mathrm{0}}\cdot \cos \left(\mathrm{2}\mathit{\pi }ft+\mathit{\varphi }\right)\cdot e^{(-\mathit{\delta }t)},\end{array}$$

where x₀ is the amplitude of the signal at t₀, f is the frequency, ϕ is the phase, and δ is the damping coefficient. The damping coefficient is calculated by two consecutive extremal values x_i and x_(i+1) of the curve, with a distance of one period T using the relation

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle \frac{x_i}{x_{(i+\mathrm{1})}}}=e^{\mathit{\delta }T}.\end{array}$$

In order to evaluate the damping characteristics of the observed system, the damping ratio

$$\begin{array}{}\text{(5)}& {\displaystyle }{\displaystyle }D={\displaystyle \frac{\mathrm{\Lambda }}{\sqrt{(\mathrm{2}\mathit{\pi }{)}^{\mathrm{2}}+{\mathrm{\Lambda }}^{\mathrm{2}}}}}\text{with}\mathrm{\Lambda }=\mathit{\delta }T=\ln \left({\displaystyle \frac{x_i}{x_{(i+\mathrm{1})}}}\right)\end{array}$$

is calculated (Niedrig and Sternberg, 2013). While every constant of the observed system remains unchanged, the variation in damping results solely from the energy dissipation due to the work performed on the eye. It is going to be demonstrated by means of laboratory tests on porcine eyes that the damping ratio of a coupled spring–mass–damper system changes with the IOP of the connected eye.

2.2 Experimental setup

The experimental setup consists of a pressure chamber with an inner volume of 70 cm³. In order to avoid resonances, the chamber has no parallel walls. Connected to the chamber are a 6.35 mm electret microphone for high SPL up to 150 dB, with a signal-to-noise ratio of 33 dB, and a full-range loudspeaker with 30 mm diameter, 8 Ω, and 2 W (see Fig. 1a). Additionally, the oscillation of the loudspeaker's diaphragm is measured by evaluating the current of an intensity-based distance sensor represented by an analog infrared reflection sensor CNY70 (Vishay). The loudspeaker, the gas volume, and the eye are considered a coupled mechanical system.

For the measurements, an enucleated porcine eye is placed on top of the pressure chamber, sealing it fully. The eye lies on a circular vent, with the cornea facing the inside of the chamber, and is fixed with two instant adhesive spots. It is penetrated by a cannula (1.1 mm outer diameter, flow-rate 61 mL min⁻¹) connected to a liquid column of 0.9 % saline solution. The cannula was inserted into the eye from the side; about 7 mm behind the limbus, reaching into the vitreous body; see Fig. 1b. The pressure level can be adjusted between 5 and 60 mmHg, in order to determine the influence of IOP changes on the damping characteristic of the system. The measurements start at a low level of 5 mmHg, and begin 60 s after altering the column to allow for pressure equalization. In order to preclude a negative effect of prior measurements on the same specimen, hysteresis tests are done directly after initial measurements. During hysteresis tests, the IOP is successively lowered from the maximum value of 60 mmHg and the measurements at intermediate IOP levels are repeated. For hysteresis tests the vitreous body was replaced by 0.9 % saline solution; otherwise no decrease in pressure could be measured because of the vitreous body blocking the entrance of the cannula.

The porcine eyes used for the experiment have been enucleated about 90 min prior to the measurements. To avoid changes in material behavior due to dry-out effects of sclera and cornea, the eyes have been kept in a 0.9 % saline solution, and can be considered freshly enucleated. In order to achieve best comparability, the eyes have been carefully cleansed from fat and muscular tissue prior to the examination. The weight was recorded before and after regular measurements with the vitreous body in place. It was found that the eyes weigh on average 7.54±0.79 g before and 7.85±0.74 g after the measurement, gaining a weight of 0.31±0.09 g on average.

In order to achieve an optimal rectangular signal, the excitation signal for the loudspeaker is generated by two voltage sources. They are switched successively between −2.5 V (duration 1 ms) and 3.5 V (duration 2 ms) via external electronics. Hereby the speaker generates a pressure pulse of 1000 Pa within the chamber. After excitation, the speaker's oscillation can settle freely. The pulse response of the coupled mechanical system is analyzed using the information provided by the microphone and the measured oscillation of the speaker's diaphragm (see Fig. 2). For this purpose, the analog output signals of the microphone and the infrared reflection sensor are sampled with a frequency of 51.2 kHz and digitized with 24 bit A ∕ D converters. Changes between successive measurements exclusively concern the adjustment of the IOP level. Accordingly, any systematic change in the system's response can be attributed to the IOP level. Considering formulae (1) and (5), it is expected that the damping of the coupled mechanical system changes according to the IOP adjustments. In order to test the reproducibility of the measurements, at least 18 pressure pulses are recorded for each IOP level and specimen.

3 Results

The speaker's voltage and current, the output signal of the microphone and the movement of the speaker's diaphragm have been recorded for 9 eyes at 10 IOP levels and 18 impulses each. It was found that the microphone signal and the oscillation of the speaker's diaphragm provide information about the IOP in the specimen.

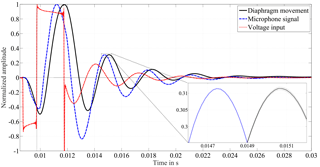
Figure 2 Each of the curves represents the mean of 18 individual impulses that were recorded at one example IOP level. Confidence bounds with the expanded standard uncertainty of the mean (coverage factor k=2) are drawn by two adjacent lines that surround the mean values (only visible in close-up view). The voltage input causes the speaker to oscillate, i.e., a movement of the diaphragm of the speaker results. The pressure in the closed chamber is monitored with a microphone.

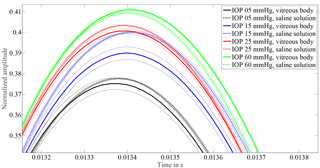
Figure 3 Allocation of curves measured from eyes with vitreous body and measurements after vitrectomy with 0.9 % saline solution as replacement for the vitreous body. A similar ascending order of the individual IOP response proves that the principle works on eyes with the vitreous body in place. Except for 15 mmHg amplitude, heights only change by 0.3 % with respect to the excitation pulse. The frequency changes by 1.5 to 3 %.

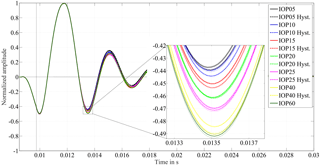
Figure 4 Diaphragm displacement detected with a Vishay CNY70 reflection sensor for porcine eye no. 3 for IOP values between 5 and 60 mmHg. The dashed-line curves are recorded when the pressure was consecutively lowered, for the hysteresis test. The close-up view of the first extremal value after excitation demonstrates the IOP dependent damping behavior. The higher the adjusted IOP is, the higher the amplitude is, the lower the damping ratio is. For hysteresis tests the vitreous body was replaced by 0.9 % saline solution, to avoid blocking effects of the cannula.

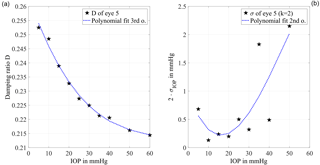
Figure 5 (a) The damping ratio calculated with formulae (4) and (5) is plotted against the IOP level. The sensitivity is represented by the slope of the curve which has the largest absolute value between 10 and 35 mmHg. For higher IOP levels the absolute value of the slope decreases, which shows a lower sensitivity. The curve is fitted by a third-order polynomial (R²=0.992) for the error propagation calculation. (b) The derived standard uncertainty of the IOP determination with a coverage factor k=2 is plotted against the IOP. In the range from 5 to 35 mmHg, the estimated standard uncertainty of the mean is below 1 mmHg. This confirms the feasibility of the measurement principle for clinical application.

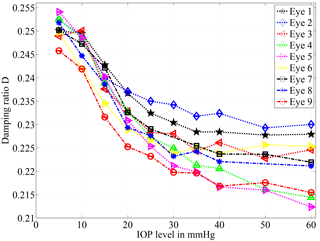
Figure 6 Damping ratio calculated according to formulae (4) and (5) for nine different porcine eyes. For all eyes the damping ratio decreases with the IOP level. The highest sensitivity is available in the range of 10 to 30 mmHg. Two outlying data points have been excluded for the eyes 7 and 8 due to artifacts. Note that error bars are drawn but too small for visualization.

3.1 Characteristics of porcine eye measurements

Figure 2 shows one sample impulse alongside the excitation signal. Each curve represents the mean of 18 individual impulses that were recorded at one sample IOP level. The voltage input causes the diaphragm of the speaker to oscillate back and forth, which can be followed via the reflection sensor. The pressure in the closed chamber is monitored with a microphone. The narrow confidence bounds display the standard uncertainty of the mean with coverage factor (k=2) and demonstrate the good reproducibility of the 18 single measurements from the microphone and the diaphragm movement. A perfect reproducibility of the input signal is crucial for the analysis of the system's behavior concerning IOP changes in the eye.

In order to verify that the change in vibration characteristic of the coupled system is free from temporal effects concerning the measurement object and procedure, hysteresis tests have been performed. When lowering the liquid column for the hysteresis test, the vitreous body blocks the entrance of the cannula, since the pressure level within the eye is higher than outside. Thus, no hysteresis test can be performed with the vitreous body in place. The influence of vitreous replacement is shown in Fig. 3. The oscillation frequency changes by 1.5 to 3 %, equal to 1–2 sample points, which is close to the resolution limit of the A ∕ D converter. The first extremum after excitation changes between 0.3 and 1 % when the vitreous body is replaced by saline solution. As a result, it was possible to demonstrate that the response of the system remains constant and equivalent IOP levels, with and without vitreous body, can be allocated.

3.2 Damping of the coupled system

The response of the coupled spring–mass–damper system, as detected by the movement of the speaker's diaphragm, is shown in Fig. 4 for the tested IOP levels. The effect of different IOP values on the system can be clearly distinguished in the close-up view of the first minimum after excitation. As a noticeable result, higher IOP values lead to higher amplitudes after excitation. Thus the order of the amplitudes represents the ascending IOP level.

On average, the standard uncertainty is 0.03 % at the extremal values successive to the excitation pulse. Figure 4 also shows the results of the hysteresis test in the dashed lines. They correspond closely to the results of the initial measurements. At the IOP levels of 20 and 25 mmHg the difference between related extrema of the hysteresis test to the initial measurement is less than 0.2 % of the excitation impulse. For the other IOP levels the differences lie within the range of 0.2 to 0.5 %. Thus, results of the hysteresis tests show the same distinguishable effect of the IOP level on the ascending order of amplitudes. This implies that the principle works irrespective of the eye's IOP history. Furthermore, it shows that material changes due to possible dry-out effects on the test bench do not influence the measurement to a significant extent. A significant change in the oscillation frequency is not observed.

The findings support the physical analogy with the pressurized ball and the assumption from formulae (1) and (5) that the major influence of the IOP can be observed in the damping of the system.

Figure 5a shows the damping ratio, plotted with respect to the IOP. It has been calculated from the excitation pulse and the following first minimum of the system response, using formulae (4) and (5). For further evaluation a third-order polynomial fit (R²=0.992) is applied, where the sensitivity regarding changes in the IOP is represented by the slope of the curve. For higher IOP levels the absolute value of the slope decreases from 0.2 % at 10 mmHg to 0.015 % at 60 mmHg, which shows a lower sensitivity.

Using an error propagation calculation, the measurement uncertainty due to random fluctuations of the damping ratio is determined. It is shown with a coverage factor of k=2 in Fig. 5b with respect to the IOP. The achievable standard uncertainty of the mean is below 0.35 mmHg from 5 to 30 mmHg with a minimum of 0.07 mmHg at 10 mmHg adjusted IOP. For IOP values above 30 mmHg the uncertainty is higher than 1 mmHg. With an estimated measurement uncertainty of significantly less than ±3 mmHg the clinical relevance of this approach is demonstrated.

For nine different eyes, a similar tendency can be observed in the calculated damping ratio of the system; see Fig. 6. Higher IOP values lead to higher amplitudes, and to a lower damping ratio accordingly. The reason for the deviant behavior of different specimens will be addressed in the discussion section.

4 Discussion

With the objective of designing a handheld self-tonometer a novel measurement approach was analyzed in a laboratory environment. The physical relation between the damping ratio of a coupled system that consists of a loudspeaker, a pressure chamber, and an enucleated porcine eye was validated. In agreement with the physical analogy it was found that higher IOP values lead to a lower damping ratio of the coupled speaker–air–eye system, resulting from the amount of converted energy of the system for deformation processes of the cornea. Individual IOP values are clearly distinguishable with this principle. The determined standard uncertainty of less than 0.35 mmHg in laboratory tests raises expectations for the currently performed in vivo study.

The sensitivity of this measurement principle is highest in the normal IOP range, between 10 and 20 mmHg (Giaconi et al., 2016), and decreases for higher IOP values. The effect is known from current tonometry methods such as the iCare tonometer (Munkwitz et al., 2008), Tono-pen (Giaconi et al., 2016), or air-puff tonometers (Derka, 1980) that the sensitivity decreases at higher IOP levels (Eklund et al., 2000; Giaconi et al., 2016; Yung et al., 2014). This is explained by the fact that the possible deformation of the eye with a constant force decreases, which leads to a lower signal-to-noise ratio. Due to stochastic deviations, the sensitivity of the measurement principle decreases proportional to the signal-to-noise ratio, which then leads to a larger measurement uncertainty. It is a challenging task for static and dynamic methods to determine elevated IOP values above 30 mmHg with a low uncertainty. Fortunately the exact determination at raised IOP levels above 30 mmHg is of low clinical relevance, as long as raised IOP levels can be precisely distinguished from IOP levels in the normal physiological range.

The hysteresis test was obligatory to confirm that the observed differences are free from artifacts of IOP adjustment or dry-out effects of the eye on the test bench. The reproducibility of the system response demonstrated that the IOP directly affects the damping. Additional examinations confirmed that the measurement principle is applicable regardless of vitreous body replacement.

Despite consistent tendencies, deviations in the damping ratio occur when different eyes are compared. The individual weight of the eyes was recorded and tested for correlation of the observed differences. In fact, the variation of the weight does not correlate well (correlation coefficient −0.3) with the damping ratio of the system. The biometric variations among the tested eyes could not be measured during the laboratory tests. As a main potential factor for the deviations, the influence of the central corneal thickness (CCT) should be analyzed, since it is known to have major impact on measurement devices based on the Imbert–Fick law (Giaconi et al., 2016; Goldmann and Schmidt, 1957; Tonnu et al., 2005). Although this approach is not based on that principle, the cornea is still the prominent structure that is reached by the pressure pulse first, even though it is not indented. It is assumed that the CCT and the curvature of the cornea influence the performed work for the deformation process. This will be addressed in the future in vivo measurements, by recording the participants' biometric parameters with ophthalmic measurement devices. It is desired to bring a handheld self-tonometer with the above concept to market within the next 5 years.

5 Conclusions

The results of the laboratory examinations proofed the physical analogy and demonstrated the sensitivity for the presented IOP measurement approach. With the achievable standard uncertainty of the mean of less than 0.35 mmHg in the range of 5 to 25 mmHg, the principle has a highly relevant application potential. On the basis of these results, a prototype for the handheld self-tonometer was designed, which is currently used to evaluate the measurement principle on human subjects while comparing it directly against GAT. The measurement procedure of this approach takes less than 10 s and does not require anesthetics. Through its noncontact measurement, infection risks can be reduced to a minimum. Systematic deviations resulting from biometrical factors will be important issues for future research.