The size-of-source effect in thermography

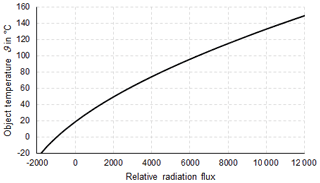
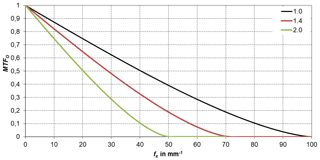
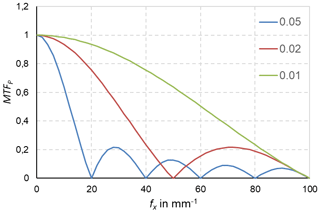
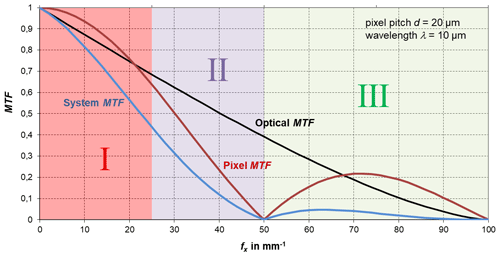
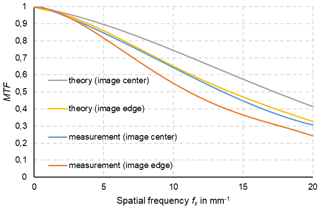
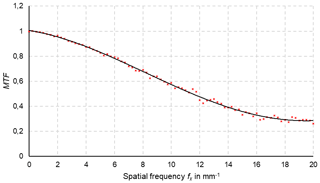
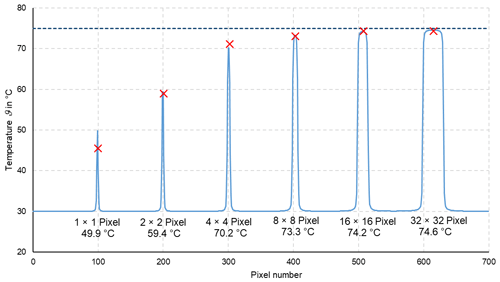
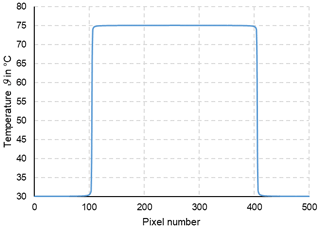
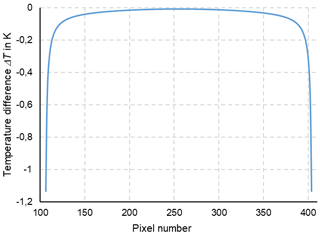
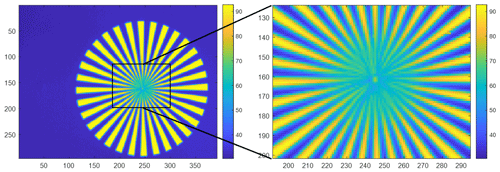
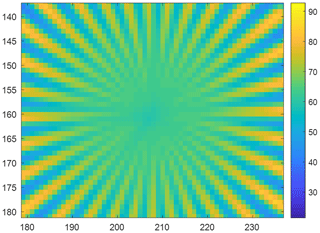
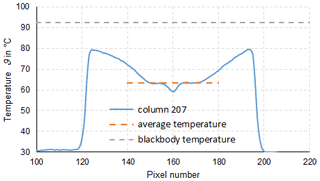
In thermometry, the displayed temperature value of an object depends on the size of the object. This behaviour, also known as the size-of-source effect (SSE), might be a major cause of measurement uncertainty in a thermoscene. The SSE is caused by diffraction, scattering, reflection, aberration and digitization in the optoelectronic propagation path. The influence of diffraction and digitization (sampling and pixelization) can be described advantageously with the modulation transfer function MTF. The system MTF of an uncooled camera is determined by the diffraction in the lens (optical MTF) and the averaging of the radiation over the pixel area (pixel MTF). If the system MTF is known, the contrast reduction and, thus, the SSE can be calculated. Especially with very small objects, e.g. hotspots creating an image covering less than 4 pixel × 4 pixel on the focal plane, the displayed temperatures are much too low. When imaging large objects, such as area blackbodies, not only the edge areas are affected, but also the entire image. Finally, the contrast reduction by the MTF is explained by means of a complex scene (Siemens star).

1 Introduction

The size-of-source effect (SSE) in pyrometry might be a major cause of temperature measurement uncertainty. It describes the effect by which the measurement signal and thus the temperature show a change in conjunction with changing size of the measured object. Its cause is diffraction, scattering, reflection and aberration of the infrared radiation to be measured in the optical channel. In pyrometry, this effect is well understood and extensively described in the literature, e.g. in Gutschwager et al. (2008) and Machin and Sergienko (2001).

This effect also occurs in thermography. The displayed temperature of an object in the thermoscene depends on the size of the object. Particularly for very small objects (forming an image of less than 4 pixel × 4 pixel), the temperatures measured are regularly erroneous. Alongside the previously mentioned reasons for the SSE, in thermography the digitization of the thermal image (sampling and pixelization) provides a further important cause. In principle, the SSE represents a reduction in contrast and can be described as such. In contrast to scattering, reflection and aberration, diffraction and digitization can be described with the modulation transfer function MTF, as is common in image processing.

In the following, this contrast reduction is described for an uncooled thermal imaging camera using the MTF. With the aid of the MTF, the SSE can then be calculated for very small and very large objects and subsequently a scene (Siemens star) presented to measure the image quality.

Figure 1 Relative radiation flux vs. temperature for the uncooled infrared camera used.

Figure 2 Optical MTF for a wavelength  λ of 10 µm. Parameter: f number k.

Figure 3 Pixel MTF. Parameter: pixel width a in µm.

Figure 4 Optical, pixel and resulting system MTF for an uncooled thermal-imaging camera.

Figure 5 Comparison of the theoretical and measured MTF. QVGA microbolometer camera with 25 µm pixel size; lens f/1.0–18 mm.

Figure 6 Measured values and regression curve of the MTF. Red crosses: measured values. Black line: regression polynomial third degree. QVGA microbolometer camera with 25 µm pixel size; lens f/1.0–18 mm; signal–noise ratio SNR at f_x = 0 mm⁻¹ about 5000.

2 MTF of an uncooled thermal imaging camera

For optoelectronic systems, the optical transfer function OTF describes the image quality (DIN ISO 9335, 2015; DIN ISO 15529, 2010). The modulation transfer function MTF is the magnitude of the OTF (Budzier and Gerlach, 2011). In uncooled infrared cameras with microbolometers, the system MTF is obtained through multiplication of the optical MTF of the lens used and the pixel MTF.

At this point it must be explicitly stated that all considerations of the MTF always refer to the radiation flux and not to temperatures. Thus, an MTF of 0 means an averaging of the radiation in the image, which does not correspond to the average value of the temperatures in the thermal image due to the non-linear correlation of radiation flux and temperature (Planck's radiation law).

Figure 7 Temperatures of a hotspot shown in the thermal image. Dashed line: true hotspot temperature (75 ^∘C). Red crosses: measured values. Parameter: hotspot size in scene; temperature information: maximum hotspot temperatures.

Figure 8 Profile of the thermal image of an ideal blackbody radiator at 75 ^∘C, 300 pixels wide.

Figure 9 Temperature difference of the blackbody surface between the ideal blackbody and profile (Fig. 8); edge pixels 106 and 406 not shown (ΔT = −8.4 K).

Figure 10 Photo of the Siemens star screen, diameter 110 mm.

In addition to the thermal image (temperature in ^∘C), an infrared camera also outputs values proportional to the radiation flux, which correspond to the digital voltages of the pixels. These values are converted to temperatures in the calibration process and are called relative radiant flux. Figure 1 shows the measured relationship between the object temperature and the relative radiation flux of the uncooled infrared camera used. The relationship shown is typical for uncooled infrared cameras. However, since the exact values are very specific for each camera, these relationships are determined during the calibration process of the individual infrared camera (Budzier and Gerlach, 2015).

2.1 Optical MTF

In the far-infrared spectrum (wavelengths from 8 to 14 µm), the lenses are essentially limited by diffraction; that is, the optical resolution is determined by the Fraunhofer diffraction. Thus, for the optical MTF the following applies (Hecht, 2002):

$$\begin{array}{}\text{(1)}& {\mathrm{MTF}}_{\mathrm{O}}\left(f_x\right)={\displaystyle \frac{\mathrm{2}}{\mathit{\pi }}}\left[\arccos \left(\mathit{\lambda }k{f}_x\right)-\mathit{\lambda }k{f}_x\sqrt{\mathrm{1}-(\mathit{\lambda }k{f}_x{)}^{\mathrm{2}}}\right],\end{array}$$

with spatial frequency f_x, wavelength λ and f number k.

Figure 2 shows the optical MTF for ordinary f numbers. It has to be noted here that already at very low spatial frequencies a clear reduction in contrast occurs.

2.2 Pixel MTF

A pixel integrates the incident radiation over its area. From this is derived the pixel MTF, also called the geometric MTF or detector MTF, by Daniels (2018):

$$\begin{array}{}\text{(2)}& {\mathrm{MTF}}_{\mathrm{P}}=\left|{\displaystyle \frac{\sin \mathit{\pi }a{f}_x}{\mathit{\pi }a{f}_x}}\right|,\end{array}$$

with pixel width a. Figure 3 shows the pixel MTF for various pixel widths. At the zero points of the pixel MTF, the spatial period is the same size as the pixel width. At the zeroes, a phase jump in the OTF of 180^∘ also occurs.

For the sake of simplicity, in the following, the pixel width is set equal to the pixel raster size, in full cognizance of the fact that the fill factors of real microbolometers are less than 1.

2.3 System MTF

The system MTF is the product of the various MTF components:

$$\begin{array}{}\text{(3)}& {\mathrm{MTF}}_{\mathrm{S}}\left(f_x\right)={\mathrm{MTF}}_{\mathrm{O}}\left(f_x\right)\cdot {\mathrm{MTF}}_{\mathrm{P}}\left(f_x\right).\end{array}$$

The system MTF is to be interpreted using an example (Fig. 4). In Fig. 4, three characteristic regions are labelled in colour. Region I starts at spatial frequency 0 (uniform illumination of the thermal image) and ends at the Nyquist frequency (f_xN = 25 mm⁻¹). In this region, the display of spatial content in the thermal image is geometrically correct. It is the actual working range. However, the system MTF at the Nyquist frequency is only approx. 0.45. The effect of this pronounced low-pass behaviour on the temperature measurement is discussed in Sect. 3.

Spatial frequencies above the Nyquist limit are incorrectly sampled (region II) because aliasing occurs. From this, the most varied artefacts can arise.

At spatial frequencies above the spatial frequency of the first zero of the pixel MTF (f_x > 50 mm⁻¹), spurious resolution occurs (region III). This means that warmer objects appear colder than the image average. This can occur in practice where hotspots in the image are less than half a pixel in width.

Figure 11 Thermal image of the Siemens star in front of a surface blackbody radiator at 92 ^∘C taken with an uncooled QVGA thermal imaging camera; lens f/1.0–18 mm, distance from camera to screen 25 cm.

2.4 Measurement of the MTF

In this case the measurement of the MTF is carried out at an edge (Budzier and Gerlach, 2011). The image at the edge is spatially differentiated, Fourier-transformed and then normalized. The result then forms the system MTF. Figure 5 shows a comparison of theoretical values (MTF given by the lens manufacturer multiplied by the pixel MTF_P) and the measured MTF. The MTF was measured using a lens with a field of view FOV of 24^∘ and an f number k of 1. In each case, MTF curves are shown at the centre of the image (angle of incidence 0^∘) and at the edge of the image (angle of incidence 12^∘). The theoretical curve at the image centre corresponds to the diffraction-limited MTF curve elucidated above. The difference between theoretical and practical values results from manufacturing and assembly tolerances. The measured curves presented are the regression curves of the measurement results. The original curves are subject to noise, particularly at lower MTF values (Fig. 6).

3 The SSE by the example of smaller and larger objects

For small objects, e.g. images of hotspots extending a few pixels in the image, the measured object temperature is always less than the actual temperature (Fig. 7). For very small objects, e.g. smaller than 4 pixel × 4 pixel in the image, significant deviations occur.

When imaging large objects, such as area radiators, not only the edges are blurred, but the entire surface is also affected (Fig. 8). For example, the profile of the hot surface is rounded (Fig. 9). The measured temperature decreases from the centre of the image of the surface to the edge. Colder objects are accordingly measured warmer than their true temperature. Colder or hotter refers to the average temperature of the thermoscene. All profiles have been calculated with the measured MTF from Fig. 5 (image centre) and for a QVGA microbolometer with a pixel size of 25 µm and a lens with f/1.0–18 mm. In addition, it has been assumed that the same MTFs apply in both the vertical and horizontal directions.

4 Representation of a complex thermoscene (Siemens star)

The Siemens star offers a good opportunity to test the quality of an optical imaging system. To this end, a suitable scene was created (Fig. 10). In the thermal image (Fig. 11) it can clearly be seen how small structures are blurred out and approach the average temperature of approx. 62 ^∘C. The small opening at the centre of the Siemens star, required for manufacture, shows 72.4 ^∘C, that is, 20 K less than the real temperature.

If the distance between the camera and the scene is increased, the structures shown on the thermal image become smaller (Fig. 12). In the profile, there is clearly an area at average temperature (MTF → 0). At the centre of the Siemens star, where there ought to be a hotspot, the temperature is below this average (Fig. 13). This is where spurious resolution occurs.

Figure 12 Thermal image (section) of the Siemens star in front of a surface blackbody radiator at 92 ^∘C taken with an uncooled QVGA thermal imaging camera with scene–camera distance 100 cm. Lens f/1.0–18 mm.

Figure 13 Measured profile through the middle of the Siemens star taken from Fig. 12.

5 Summary

The modulation transfer function MTF is suitable for explaining the phenomena of contrast reduction and the size-of-source effect (SSE). Therefore, it provides a good and above all impartial description of the image quality. The MTF of uncooled infrared cameras is determined by the diffraction of the lens and the sampling caused by the pixel size. It also allows an estimate of how large an object needs to be that the displayed temperature shows a sufficient accuracy.

The SSE leads to blurring in the image. This is of particular importance for the imaging of small objects, where the displayed temperatures are particularly incorrect. Since the size of an object in the image depends on the measuring distance, there is an apparent distance dependence of the temperature measurement. When imaging large objects, not only the edges become blurred, but the entire image is also affected.

However, other image errors such as reflections in the optical channel or defects in sensor electronics cannot be explained by the MTF.