The optimal distribution of axial strain amplitude in a piezoelectric vibrating energy harvester

This study considers the optimal distribution of strain amplitude in a piezoelectric vibrating energy harvester (PVEH) that maximizes the harvested energy. In many previous studies, it was tacitly assumed that a uniform distribution of axial strain in the piezoelectric layer ensures that the harvested energy is maximal. Though this assumption is intuitive, it was not supported by analysis. In this work, we derive and present a formal analytic proof confirming that, for a given amount of energy in the vibrating structure, a uniform distribution of strain in the piezoelectric layer ensures that the harvested energy is maximal.

1 Introduction

Piezoelectric vibrating energy harvester (PVEH) devices have been studied for over 2 decades (Erturk and Inman, 2008, 2009, 2011). These devices are becoming increasingly relevant as potential power sources for autonomous sensors and internet of things (IoT) applications. The most prevalent PVEHs are constructed from a piezoelectric unimorph, in which an elastic cantilever is coated with a thin layer of piezoelectric material. This piezoelectric layer is sandwiched between a top electrode and a bottom electrode. When the piezoelectric unimorph is subjected to base excitations at its natural frequency, the amplitude of vibrations increases. The periodic modulation of curvature in the cantilever results in periodic modulation of axial strain in the piezoelectric layer, which can be used to harvest electric energy. The amount of energy per vibration cycle that can be harvested depends on the electric load between the electrodes (e.g., resistor for direct heating and diode bridge for charging a battery) and the frequency of vibrations (Erturk and Inman, 2008, 2009, 2011; Karami et al., 2011).

For example, if the electrodes are disconnected (or connected by an infinite resistance), no charge will be transferred between the electrodes, and a maximal potential difference will develop between them. In this case, obviously, no power will be harvested. If, in contrast, the electrodes are shorted (i.e., connected by a resistor of zero resistance), a maximal amount of charge will be transferred between the electrodes, but there will be no voltage difference between them. Clearly, in this case as well, no power will be harvested.

The maximal amount of energy that can be harvested is proportional to the charge accumulated when the electrodes are shorted and the maximal voltage induced when the electrodes are disconnected (Du et al., 2017; Lustig and Elata, 2020). In general, assuming the structure vibrates at its fundamental mode, the accumulated charge is maximal when the structure is completely covered by the piezoelectric layer and electrodes. However, for disconnected electrodes, a partial coverage of the piezoelectric layer and electrode may be necessary to achieve the maximal voltage. In many PVEH devices, the amplitude of curvature in the structure is not uniform. In cantilever structures the maximal curvature occurs in vicinity of the clamped edge. Accordingly, an electrode that covers that region of the cantilever ensures that voltage is maximal. Extending the electrode towards the free edge of the cantilever will result in a reduction in voltage amplitude. It follows that there is an optimal coverage of electrodes that maximizes the harvested energy (e.g., Du et al., 2017).

In previous studies, it was identified that an optimal planform of the unimorph cantilever may result in a uniform amplitude of axial strain in the piezoelectric layer. In this case, the voltage difference between disconnected electrodes is independent of the electrode coverage, and it follows that a full coverage of electrode maximizes the harvested energy. This has been demonstrated in PVEH devices which include a dominant edge block. Some investigations used simulations to conclude that in this case, a trapezoidal planform of the PVEH is optimal, while others used experiments to demonstrate the same conclusion (Baker et al., 2005; Benasciutti et al., 2010; Chen et al., 2009; Dietl and Garcia, 2010; Gallina and Benasciutti, 2013; Jia and Seshia, 2016; Lee et al., 2009; Miller et al., 2011). In a recent publication, we presented a new model which confirms why a trapezoidal planform is optimal and which could be used for design. For a given edge block and excitation frequency, the model explicitly provides the geometry of the PVEH with no need for simulations (Salman et al., 2024a).

In the case of PVEH unimorphs that do not include a dominant edge block, a trapezoidal planform is not optimal. For this case, it has been shown that a tapered planform defined by Bessel functions ensures that the axial strain in the PVEH is uniform (Salman et al., 2024c, 2025).

In all the abovementioned investigations, it was tacitly assumed that ensuring a uniform distribution of strain amplitude in the piezoelectric layer ensures that the harvested energy is maximized. This seems to be intuitively sensible, but it appears that no formal proof of this has ever been provided.

The aim of the present study is to provide a formal proof and show that for a given amount of vibration energy in a PVEH, a uniform distribution of axial strain amplitude ensures that the harvested energy is maximal.

2 Analysis

Figure 1 presents a schematic illustration of a piezoelectric cantilever unimorph that is constructed from an elastic substrate of thickness h coated with a thin piezoelectric layer of thickness h_pe (h_pe ≪ h). The beam length is L, and the width b(x) may be non-uniform. The elastic substrate serves as a bottom electrode for the piezoelectric layer, and a thin electrode covers the entire top surface of the piezoelectric layer. In this study, we consider a piezoelectric material of the 4 mm point group (e.g., aluminium nitride, AlN, and tetragonal lead zirconite titanate, PZT) (Ikeda, 1996; Uchino, 1997), with the poling pointing in the z direction. When the unimorph is subjected to base excitation, it can be used as a PVEH device.

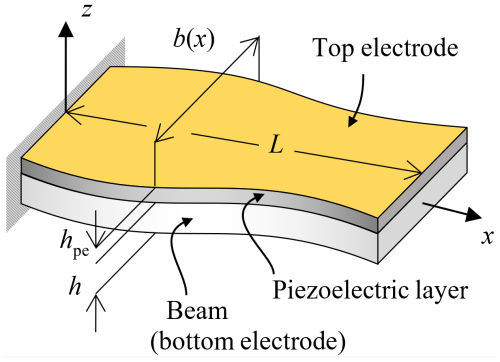
Figure 1 Schematic description of a PVEH unimorph cantilever. The unimorph is constructed from an elastic beam of length L, thickness h and non-uniform width b(x). The beam is coated with a thin piezoelectric layer of thickness h_pe that is covered by the top electrode.

This study only considers synchronous vibrations, in which the deflection (i.e., motion in the z axis) can be described as the product of a spatial mode w(x) (where w(x) is a monotonically increasing function of x) and a single harmonic function of time sin(ωt). It is tacitly assumed that the deflection mode is a cylindrical bending such that at any cross section x, the deflection w(x) is uniform (i.e., not a function of y or z).

The aim of this study is to determine the optimal distribution of strain amplitude that maximizes the energy harvested by this device. To this end, the electric energy U_E that may be harvested in one-half of a motion cycle is proportional to the product of the charge amplitude Q_Short that is transferred between the electrodes, if they are shorted (i.e., connected), and the amplitude of voltage difference V_Open between the electrodes, if they are open (i.e., disconnected), the following applies (Du et al., 2017; Lustig and Elata, 2020):

$$\begin{array}{}\text{(1)}& U_{\mathrm{E}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{Q}_{\mathrm{Short}}{V}_{\mathrm{Open}}.\end{array}$$

In Voigt notation (Ikeda, 1996; Meitzler et al., 1988), the constitutive equations of the material are given by

$$\begin{array}{}\text{(2)}& {\displaystyle }\begin{array}{rl}& \left(\begin{array}{c}{T}_{\mathrm{1}}\\ T_{\mathrm{2}}\\ T_{\mathrm{3}}\\ T_{\mathrm{4}}\\ T_{\mathrm{5}}\\ T_{\mathrm{6}}\end{array}\right)=\left(\begin{array}{cccccc}{C}_{\mathrm{11}}^E& C_{\mathrm{12}}^E& C_{\mathrm{13}}^E& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ C_{\mathrm{12}}^E& C_{\mathrm{11}}^E& C_{\mathrm{13}}^E& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ C_{\mathrm{13}}^E& C_{\mathrm{13}}^E& C_{\mathrm{33}}^E& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& C_{\mathrm{44}}^E& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& C_{\mathrm{44}}^E& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& C_{\mathrm{66}}^E\end{array}\right)\\ & \left(\begin{array}{c}{S}_{\mathrm{1}}\\ S_{\mathrm{2}}\\ S_{\mathrm{3}}\\ S_{\mathrm{4}}\\ S_{\mathrm{5}}\\ S_{\mathrm{6}}\end{array}\right)-\left(\begin{array}{ccc}\mathrm{0}& \mathrm{0}& e_{\mathrm{31}}\\ \mathrm{0}& \mathrm{0}& e_{\mathrm{31}}\\ \mathrm{0}& \mathrm{0}& e_{\mathrm{33}}\\ \mathrm{0}& e_{\mathrm{15}}& \mathrm{0}\\ e_{\mathrm{15}}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}\end{array}\right)\left(\begin{array}{c}{E}_{\mathrm{1}}\\ E_{\mathrm{2}}\\ E_{\mathrm{3}}\end{array}\right),\end{array}\text{(3)}& {\displaystyle }\begin{array}{rl}\left(\begin{array}{c}{D}_{\mathrm{1}}\\ D_{\mathrm{2}}\\ D_{\mathrm{3}}\end{array}\right)& =\left(\begin{array}{cccccc}\mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& e_{\mathrm{15}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& e_{\mathrm{15}}& \mathrm{0}& \mathrm{0}\\ e_{\mathrm{31}}& e_{\mathrm{31}}& e_{\mathrm{33}}& \mathrm{0}& \mathrm{0}& \mathrm{0}\end{array}\right)\left(\begin{array}{c}{S}_{\mathrm{1}}\\ S_{\mathrm{2}}\\ S_{\mathrm{3}}\\ S_{\mathrm{4}}\\ S_{\mathrm{5}}\\ S_{\mathrm{6}}\end{array}\right)\\ & +\left(\begin{array}{ccc}{\mathit{\epsilon }}_{\mathrm{11}}^S& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& {\mathit{\epsilon }}_{\mathrm{11}}^S& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& {\mathit{\epsilon }}_{\mathrm{33}}^S\end{array}\right)\left(\begin{array}{c}{E}_{\mathrm{1}}\\ E_{\mathrm{2}}\\ E_{\mathrm{3}}\end{array}\right).\end{array}\end{array}$$

Here T_i is the component of stress, S_i is the component of strain, $C_{ij}^E$ is the component of the stiffness matrix (stiffness at constant electric field), E_k is the component of the electric field, D_k is the component of the electric displacement, e_ki is the component of the piezoelectric coefficient matrix and ε_kl is the component of the permittivity matrix under constant strain (the indices i and j take the values of 1 through 6, and the indices k and l take the values of 1 through 3).

In the piezoelectric layer, the poling points in the z direction such that material directions 1, 2 and 3 are parallel to the spatial axes x, y and z, respectively. According to the Euler–Bernoulli beam theory and considering that the piezoelectric layer is thin, we may deduce that within the piezoelectric layer several terms vanish. Specifically, within this layer, the shear strains and stresses are zero (i.e., $S_{\mathrm{4}}=S_{\mathrm{5}}=S_{\mathrm{6}}=$ 0 and $T_{\mathrm{4}}=T_{\mathrm{5}}=T_{\mathrm{6}}=$ 0), and the transverse stress T₃ is zero because the top surface of the unimorph is stress-free. Furthermore, due to geometrical considerations, the components of the electric field and electric displacement (i.e., flux) along the x and y axes vanish (i.e., $E_{\mathrm{1}}=E_{\mathrm{2}}=$ 0 and $D_{\mathrm{1}}=D_{\mathrm{2}}=$ 0). Finally, for cylindrical bending, we may assume that S₂= 0, and that S₁ is not a function of y. Because the piezoelectric layer is thin, we may also consider S₁ within the piezoelectric layer to be independent of z (this is known as the small-piezoelectricity assumption; Krommer, 2001; Tiersten, 1969) so that overall S₁(x) is uniform in each cross section, though it may vary along the beam.

With these conditions, Eqs. (2) and (3) reduce to the following two coupled equations:

$$\begin{array}{}\text{(4)}& {\displaystyle }{T}_{\mathrm{3}}\left(x\right)=\mathrm{0}=C_{\mathrm{13}}^E{S}_{\mathrm{1}}\left(x\right)+C_{\mathrm{33}}^E{S}_{\mathrm{3}}\left(x\right)-e_{\mathrm{33}}{E}_{\mathrm{3}},\text{(5)}& {\displaystyle }{D}_{\mathrm{3}}\left(x\right)=e_{\mathrm{31}}{S}_{\mathrm{1}}\left(x\right)+e_{\mathrm{33}}{S}_{\mathrm{3}}\left(x\right)+{\mathit{\epsilon }}_{\mathrm{33}}^S{E}_{\mathrm{3}}.\end{array}$$

Here the unknowns are S₁, S₃, E₃ and D₃. The axial strain S₁ is directly related to the deflection curvature, and its distribution is determined by the distributions of inertia and of bending rigidity along the beam. In this investigation, we do not wish to deduce the explicit functional form of S₁ from the dynamics of the problem. Rather, we wish to find the optimal distribution of S₁ for energy harvesting. Later, if it is of any interest, we may attempt to design a cantilever with specific distributions of inertia and of bending rigidity such that in periodic vibrations at some frequency ω, the distribution of the axial strain S₁ will be equal to the optimal value we derived (e.g., Salman et al., 2024a). So, practically, we need to solve the two equations, Eqs. (4) and (5), for the three variables S₃, E₃ and D₃. However, as we show next, the electrostatic boundary conditions help by imposing constrains on the values of either E₃ or D₃, thus leaving only two unknowns to be solved by the two equations, Eqs. (4) and (5).

2.1 Shorted electrodes

When the electrodes are shorted, the electrostatic field in the z axis vanishes. Substituting E₃= 0 into Eq. (4) yields the relation between S₁ and S₃ for shorted electrodes:

$$\begin{array}{}\text{(6)}& S_{\mathrm{3}}\left(x\right)=-{\displaystyle \frac{C_{\mathrm{13}}^E}{C_{\mathrm{33}}^E}}{S}_{\mathrm{1}}\left(x\right).\end{array}$$

Substituting this into Eq. (5) yields

$$\begin{array}{}\text{(7)}& D_{\mathrm{3}}\left(x\right)=\left(e_{\mathrm{31}}-{\displaystyle \frac{e_{\mathrm{33}}{C}_{\mathrm{13}}^E}{C_{\mathrm{33}}^E}}\right)S_{\mathrm{1}}\left(x\right).\end{array}$$

The total charge Q_Short accumulated on the top electrode is given by

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{Q}_{\mathrm{Short}}& =\underset{x=\mathrm{0}}{\overset{L}{\int }}{D}_{\mathrm{3}}\left(x\right)b\left(x\right)\mathrm{d}x\\ & =\left(e_{\mathrm{31}}-{\displaystyle \frac{e_{\mathrm{33}}{C}_{\mathrm{13}}^E}{C_{\mathrm{33}}^E}}\right)\underset{x=\mathrm{0}}{\overset{L}{\int }}{S}_{\mathrm{1}}\left(x\right)b\left(x\right)\mathrm{d}x.\end{array}\end{array}$$

2.2 Open electrodes

From Eq. (4), it follows that

$$\begin{array}{}\text{(9)}& E_{\mathrm{3}}={\displaystyle \frac{C_{\mathrm{13}}^E}{e_{\mathrm{33}}}}{S}_{\mathrm{1}}\left(x\right)+{\displaystyle \frac{C_{\mathrm{33}}^E}{e_{\mathrm{33}}}}{S}_{\mathrm{3}}\left(x\right).\end{array}$$

Substituting this into Eq. (5) yields

$$\begin{array}{}\text{(10)}& \begin{array}{rl}{D}_{\mathrm{3}}\left(x\right)& =\left(e_{\mathrm{31}}+{\mathit{\epsilon }}_{\mathrm{33}}^S{\displaystyle \frac{C_{\mathrm{13}}^E}{e_{\mathrm{33}}}}\right)S_{\mathrm{1}}\left(x\right)\\ & +\left(e_{\mathrm{33}}+{\mathit{\epsilon }}_{\mathrm{33}}^S{\displaystyle \frac{C_{\mathrm{33}}^E}{e_{\mathrm{33}}}}\right)S_{\mathrm{3}}\left(x\right).\end{array}\end{array}$$

The total charge Q_Open accumulated on the top electrode is given by

$$\begin{array}{}\text{(11)}& \begin{array}{rl}{Q}_{\mathrm{Open}}& =\underset{x=\mathrm{0}}{\overset{L}{\int }}{D}_{\mathrm{3}}\left(x\right)b\left(x\right)\mathrm{d}x\\ & =\left(e_{\mathrm{31}}+{\mathit{\epsilon }}_{\mathrm{33}}^S{\displaystyle \frac{C_{\mathrm{13}}^E}{e_{\mathrm{33}}}}\right)\underset{x=\mathrm{0}}{\overset{L}{\int }}{S}_{\mathrm{1}}\left(x\right)b\left(x\right)\mathrm{d}x\\ & +\left(e_{\mathrm{33}}+{\mathit{\epsilon }}_{\mathrm{33}}^S{\displaystyle \frac{C_{\mathrm{33}}^E}{e_{\mathrm{33}}}}\right)\underset{x=\mathrm{0}}{\overset{L}{\int }}{S}_{\mathrm{3}}\left(x\right)b\left(x\right)\mathrm{d}x.\end{array}\end{array}$$

However, when the electrodes are disconnected (i.e., open), charge cannot migrate from one electrode to the other, and therefore Q_Open must be identically zero. Consequently, by setting Q_Open= 0, it follows from Eq. (11) that

$$\begin{array}{}\text{(12)}& \underset{x=\mathrm{0}}{\overset{L}{\int }}{S}_{\mathrm{3}}\left(x\right)b\left(x\right)\mathrm{d}x=-{\displaystyle \frac{\left(e_{\mathrm{31}}+{\mathit{\epsilon }}_{\mathrm{33}}^S\frac{C_{\mathrm{13}}^E}{e_{\mathrm{33}}}\right)}{\left(e_{\mathrm{33}}+{\mathit{\epsilon }}_{\mathrm{33}}^S\frac{C_{\mathrm{33}}^E}{e_{\mathrm{33}}}\right)}}\underset{x=\mathrm{0}}{\overset{L}{\int }}{S}_{\mathrm{1}}\left(x\right)b\left(x\right)\mathrm{d}x.\end{array}$$

Since the electrostatic potential over each of the electrodes is uniform, it follows that E₃(x) is also uniform. Multiplying Eq. (4) by b(x) and integrating along the cantilever yields

$$\begin{array}{}\text{(13)}& \begin{array}{rl}{E}_{\mathrm{3}}\underset{x=\mathrm{0}}{\overset{L}{\int }}b\left(x\right)\mathrm{d}x& ={\displaystyle \frac{C_{\mathrm{13}}^E}{e_{\mathrm{33}}}}\underset{x=\mathrm{0}}{\overset{L}{\int }}{S}_{\mathrm{1}}\left(x\right)b\left(x\right)\mathrm{d}x\\ & +{\displaystyle \frac{C_{\mathrm{33}}^E}{e_{\mathrm{33}}}}\underset{x=\mathrm{0}}{\overset{L}{\int }}{S}_{\mathrm{3}}\left(x\right)b\left(x\right)\mathrm{d}x.\end{array}\end{array}$$

Substituting Eq. (12) into Eq. (13) yields

$$\begin{array}{}\text{(14)}& \begin{array}{rl}{E}_{\mathrm{3}}\underset{x=\mathrm{0}}{\overset{L}{\int }}b\left(x\right)\mathrm{d}x& =\left[{\displaystyle \frac{C_{\mathrm{13}}^E}{e_{\mathrm{33}}}}-{\displaystyle \frac{C_{\mathrm{33}}^E}{e_{\mathrm{33}}}}{\displaystyle \frac{\left(e_{\mathrm{31}}+{\mathit{\epsilon }}_{\mathrm{33}}^S\frac{C_{\mathrm{13}}^E}{e_{\mathrm{33}}}\right)}{\left(e_{\mathrm{33}}+{\mathit{\epsilon }}_{\mathrm{33}}^S\frac{C_{\mathrm{33}}^E}{e_{\mathrm{33}}}\right)}}\right]\\ & \underset{x=\mathrm{0}}{\overset{L}{\int }}{S}_{\mathrm{1}}\left(x\right)b\left(x\right)\mathrm{d}x.\end{array}\end{array}$$

It follows that the voltage V_Open is given by

$$\begin{array}{}\text{(15)}& \begin{array}{rl}& V_{\mathrm{Open}}=-h_{\mathrm{pe}}{E}_{\mathrm{3}}=-h_{\mathrm{pe}}\left[{\displaystyle \frac{C_{\mathrm{13}}^E}{e_{\mathrm{33}}}}-{\displaystyle \frac{C_{\mathrm{33}}^E}{e_{\mathrm{33}}}}{\displaystyle \frac{\left(e_{\mathrm{31}}+{\mathit{\epsilon }}_{\mathrm{33}}^S\frac{C_{\mathrm{13}}^E}{e_{\mathrm{33}}}\right)}{\left(e_{\mathrm{33}}+{\mathit{\epsilon }}_{\mathrm{33}}^S\frac{C_{\mathrm{33}}^E}{e_{\mathrm{33}}}\right)}}\right]\\ & {\displaystyle \frac{\underset{x=\mathrm{0}}{\overset{L}{\int }}{S}_{\mathrm{1}}\left(x\right)b\left(x\right)\mathrm{d}x}{\underset{x=\mathrm{0}}{\overset{L}{\int }}b\left(x\right)\mathrm{d}x}}.\end{array}\end{array}$$

3 The optimal axial strain that maximizes the harvested energy

In the previous section, we derived expressions for the voltage generated for open electrodes V_Open and the charge transferred for shorted electrodes Q_Short.

Substituting these expressions from Eqs. (8) and (15) into Eq. (1) yields

$$\begin{array}{}\text{(16)}& U_{\mathrm{E}}=\mathit{\alpha }{\displaystyle \frac{{\left(\underset{x=\mathrm{0}}{\overset{L}{\int }}{S}_{\mathrm{1}}\left(x\right)b\left(x\right)\mathrm{d}x\right)}^{\mathrm{2}}}{\underset{x=\mathrm{0}}{\overset{L}{\int }}b\left(x\right)\mathrm{d}x}},\end{array}$$

where α is a scalar that depends on material parameters and the thickness of the piezoelectric layer:

$$\begin{array}{}\text{(17)}& \mathit{\alpha }=-{\displaystyle \frac{h_{\mathrm{pe}}}{\mathrm{2}}}\left(e_{\mathrm{31}}-{\displaystyle \frac{e_{\mathrm{33}}{C}_{\mathrm{13}}^E}{C_{\mathrm{33}}^E}}\right)\left[{\displaystyle \frac{C_{\mathrm{13}}^E}{e_{\mathrm{33}}}}-{\displaystyle \frac{C_{\mathrm{33}}^E}{e_{\mathrm{33}}}}{\displaystyle \frac{\left(e_{\mathrm{31}}+{\mathit{\epsilon }}_{\mathrm{33}}^S\frac{C_{\mathrm{13}}^E}{e_{\mathrm{33}}}\right)}{\left(e_{\mathrm{33}}+{\mathit{\epsilon }}_{\mathrm{33}}^S\frac{C_{\mathrm{33}}^E}{e_{\mathrm{33}}}\right)}}\right].\end{array}$$

The mechanical elastic energy stored in the beam due to bending is given by

$$\begin{array}{}\text{(18)}& U_{\mathrm{M}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\underset{x=\mathrm{0}}{\overset{L}{\int }}{E}_{\mathrm{Y}}I\left(x\right)\mathit{\kappa }(x{)}^{\mathrm{2}}\mathrm{d}x.\end{array}$$

Here κ(x) is the bending curvature along the beam, E_Y is the Young modulus and $I=b\left(x\right)h^{\mathrm{3}}/\mathrm{12}$ is the second moment of the cross section at location x.

The axial strain S₁(x) in the piezoelectric layer, at a given cross section x, is given by

$$\begin{array}{}\text{(19)}& S_{\mathrm{1}}\left(x\right)=-{\displaystyle \frac{h}{\mathrm{2}}}\mathit{\kappa }\left(x\right).\end{array}$$

Extracting κ(x) from Eq. (19) and substituting it into Eq. (18) yields

$$\begin{array}{}\text{(20)}& U_{\mathrm{M}}=\mathit{\beta }\underset{x=\mathrm{0}}{\overset{L}{\int }}{S}_{\mathrm{1}}^{\mathrm{2}}\left(x\right)b\left(x\right)\mathrm{d}x,\end{array}$$

where $\mathit{\beta }=E_{\mathrm{Y}}h/\mathrm{6}$.

Now, we wish to find the axial strain distribution function S₁(x), which will maximize the electrostatic energy U_E for an arbitrary distribution of width b(x). This can be written in the following variational notation:

$$\begin{array}{}\text{(21)}& J\left[S_{\mathrm{1}}\left(x\right)\right]=U_{\mathrm{E}},\end{array}$$

where J is a functional of the argument S₁(x). However, we aim to find the maximal electrostatic energy for all possible distributions of S₁(x), which are associated with the same specific mechanical elastic energy $U_{\mathrm{M}}^{*}$.

This can be done by considering a constrained Lagrangian with a Lagrange multiplier λ:

$$\begin{array}{}\text{(22)}& J_{\mathit{\lambda }}\left[S_{\mathrm{1}}\left(x\right),\mathit{\lambda }\right]=J\left[S_{\mathrm{1}}\left(x\right)\right]-\mathit{\lambda }\cdot \left(U_{\mathrm{M}}\left[S_{\mathrm{1}}\right(x\left)\right]-U_{\mathrm{M}}^{*}\right),\end{array}$$

which yields

$$\begin{array}{}\text{(23)}& J_{\mathit{\lambda }}\left[S_{\mathrm{1}}\left(x\right),\mathit{\lambda }\right]=U_{\mathrm{E}}-\mathit{\lambda }\cdot \left(U_{\mathrm{M}}-U_{\mathrm{M}}^{*}\right).\end{array}$$

Substituting Eqs. (16) and (20) into Eq. (23) yields

$$\begin{array}{}\text{(24)}& \begin{array}{rl}{J}_{\mathit{\lambda }}\left[S_{\mathrm{1}}\left(x\right),\mathit{\lambda }\right]& =\mathit{\alpha }{\displaystyle \frac{{\left(\underset{x=\mathrm{0}}{\overset{L}{\int }}{S}_{\mathrm{1}}\left(x\right)b\left(x\right)\mathrm{d}x\right)}^{\mathrm{2}}}{\underset{x=\mathrm{0}}{\overset{L}{\int }}b\left(x\right)\mathrm{d}x}}\\ & -\mathit{\lambda }\cdot \left(\mathit{\beta }\underset{x=\mathrm{0}}{\overset{L}{\int }}{S}_{\mathrm{1}}^{\mathrm{2}}\left(x\right)b\left(x\right)\mathrm{d}x-U_{\mathrm{M}}^{*}\right).\end{array}\end{array}$$

Applying the first variation for the functional J_λ (Eq. 24) with respect to S₁(x) and λ yields

$$\begin{array}{}\text{(25)}& \begin{array}{rl}\mathit{\delta }{J}_{\mathit{\lambda }}& =\mathrm{2}\underset{x=\mathrm{0}}{\overset{L}{\int }}\left\{\mathit{\alpha }{\displaystyle \frac{\underset{x^{\prime }=\mathrm{0}}{\overset{L}{\int }}{S}_{\mathrm{1}}\left(x^{\prime }\right)b\left(x^{\prime }\right)\mathrm{d}{x}^{\prime }}{\underset{x^{\prime }=\mathrm{0}}{\overset{L}{\int }}b\left(x^{\prime }\right)\mathrm{d}{x}^{\prime }}}-\mathit{\lambda }\mathit{\beta }\cdot S_{\mathrm{1}}\left(x\right)\right\}\\ & b\left(x\right)\cdot \mathit{\delta }{S}_{\mathrm{1}}\left(x\right)\mathrm{d}x-\mathit{\delta }\mathit{\lambda }\cdot \left\{\mathit{\beta }\underset{x=\mathrm{0}}{\overset{L}{\int }}{S}_{\mathrm{1}}^{\mathrm{2}}\left(x\right)b\left(x\right)\mathrm{d}x-U_{\mathrm{M}}^{*}\right\}.\end{array}\end{array}$$

Our goal is to identify the function form of S₁(x) at which the electrostatic energy reaches its maximum. Therefore, according to Eq. (25), the variation must be equal to zero for any δS₁(x) and any δλ. This requires that each one of the expressions that appear in curly brackets vanish given that b(x) cannot be zero.

It follows that

$$\begin{array}{}\text{(26)}& {\displaystyle }{S}_{\mathrm{1}}\left(x\right)={\displaystyle \frac{\mathit{\alpha }}{\mathit{\lambda }\mathit{\beta }}}{\displaystyle \frac{\underset{x^{\prime }=\mathrm{0}}{\overset{L}{\int }}{S}_{\mathrm{1}}\left(x^{\prime }\right)b\left(x^{\prime }\right)\mathrm{d}{x}^{\prime }}{\underset{x^{\prime }=\mathrm{0}}{\overset{L}{\int }}b\left(x^{\prime }\right)\mathrm{d}{x}^{\prime }}}=\mathrm{const},\text{(27)}& {\displaystyle }{U}_{\mathrm{M}}^{*}=\mathit{\beta }\underset{x=\mathrm{0}}{\overset{L}{\int }}{S}_{\mathrm{1}}^{\mathrm{2}}\left(x\right)b\left(x\right)\mathrm{d}x.\end{array}$$

Equation (26) determines that S₁(x) must be uniform and thus independent of x. Therefore, it follows from the same equation that

$$\begin{array}{}\text{(28)}& \mathit{\lambda }={\displaystyle \frac{\mathit{\alpha }}{\mathit{\beta }}}.\end{array}$$

Substituting the value of λ into Eq. (26) yields the solution for the axial strain S₁(x) for the stationary (maximal) electrostatic energy:

$$\begin{array}{}\text{(29)}& S_{\mathrm{1}}\left(x\right)=\sqrt{{\displaystyle \frac{U_{\mathrm{M}}^{*}}{\mathit{\beta }\underset{x=\mathrm{0}}{\overset{L}{\int }}b\left(x\right)\mathrm{d}x}}}.\end{array}$$

4 Discussion and conclusion

In this study, we consider flexural vibrations in the transverse direction of the PVEH unimorph beam and specifically have the fundamental mode in mind. The same structure may of course vibrate in higher modes of transverse flexural vibrations as well as in other modes, such as lateral flexural vibrations and torsional (i.e., twisting) vibrations. In recent publications (Salman et al., 2024a, 2025), we investigated the optimal planform of a PVEH unimorph that maximizes the harvested energy. In those studies, the electrode covers the entire top side of the unimorph. In these cases, higher modes of transverse flexural vibrations are not optimal for harvesting energy since the axial strain S₁ cannot be uniform (i.e., due to reversal of strain polarity at nodal points). Furthermore, if the planform of the unimorph is symmetric around the beam axis (as is often the case), then sideways deflections and torsional deformations are also ineffective for energy harvesting because they would result in a zero average value of S₁ in the piezoelectric layer.

Another important issue to discuss is how accurate the assumption that bending is cylindrical is, which is the justification for ignoring the lateral strain S₂. To this end, the analysis of Kaldor and Noyan (2002) is relevant, but in any case, in most applications in microelectromechanical systems (MEMS) the piezoelectric layer is deposited over a single crystalline silicon substrate with the beam axis in the stiffer [110] direction. In this [110] direction, the Poisson ratio is ν= 0.064, which means anticlastic bending is marginal (Salman et al., 2024b).

In our analysis, we only consider synchronous vibrations, in which the deflection is a product of a spatial mode and a single harmonic function of time. In many realistic scenarios, vibration may be better described as quasiperiodic, which includes many modes for which the different frequencies are not commensurate (i.e., the ratios between the frequencies is not a rational number). Obviously, in this case, the axial strain S₁ cannot be uniform, and therefore for these cases, the analysis is not applicable.

This study presents a formal proof, showing that for a given amount of mechanical elastic energy stored in a PVEH, a uniform axial strain distribution within the thin piezoelectric layer maximizes the electrostatic energy. By designing a PVEH with specific distributions of inertia and of bending rigidity, we may achieve a uniform distribution of the axial strain S₁ in the piezoelectric layer, resulting in a maximal electrostatic energy that can be harvested by the PVEH.