Homogenous static magnetic field coils dedicated to portable nuclear magnetic resonance for agronomic studies

Nuclear magnetic resonance (NMR) experiments are usually carried out at very high and homogenous magnetic fields. However, portable systems have emerged in recent years at low fields, offering many advantages like easier maintenance and open design that permit us to imagine a variety of coil configurations in order to maximize the homogeneity of the static field B₀ and the radio-frequency field B₁. The wire winding distribution based on space harmonics suppression (SHS) of the cosine current density distribution offers new possibilities of producing homogenous static fields B₀. In this work, an extension of the SHS method, allowing homogeneity enhancement and flexibility of the coil design, is presented. The efficiency of the method is demonstrated through the construction of homogenous magnetic field coils dedicated to a very low magnetic field (8 mT) ¹H NMR spectrometer. The performance of these coils in terms of magnetic field intensity and homogeneity as well as self-heating behavior is compliant with in planta experiments for agronomic studies.

1 Introduction

Global warming has increased the occurrence of stress in living plants, which forces them to adapt to the environmental conditions. This induces some modifications in growth and composition at physiological and biochemical levels (Osakabe et al., 2014). Due to the wide biodiversity of some plants, like sorghum, one needs to perform a study of the behavior for each species. The possibility of studying the local responses of plants to biotic and abiotic stress is limited since current anatomical and biochemical methods are destructive and do not allow us to investigate plants.

Otherwise, nuclear magnetic resonance (NMR) offers the possibility of non-invasively and quantitatively measuring targeted nuclei like H, C, and N in plants (Van As and Schaafsma, 1984) and some of their physical properties like M₀, T₁, T₂, diffusion and water velocity. The ¹H NMR signal is roughly quadratically dependent on the intensity of the magnetic field (Vo-Dinh, 2002). This consideration has historically oriented the NMR spectrometer design to higher magnetic fields, up to 31 T (Yoshida and Kramer, 2012), in order to take advantage of a high signal-to-noise ratio (SNR). Nevertheless this magnetic field “race” has made the NMR magnet more and more sophisticated (cooling is mandatory, bulky and extremely heavy) and therefore not suitable to the problem of monitoring the plant's response to stress in the fields.

To address the agronomic studies in planta, the NMR instrument should be lightweight in order to be easily handled. This consideration has oriented our development toward low field NMR using resistive coils, as has been demonstrated by means of a Helmholtz coil at a few mT (Asfour, 2011).

A way to increase the magnetic field strength of the resistive coil NMR would be to take advantage of the air cooling. Unfortunately that would interact with the plant and alter its behavior. A second way would be to use water cooling at the expense of a more complicated and heavier system, which are not desirable conditions. For these reasons the use of resistive coil cooling by natural convection has been considered.

The NMR instrument will be dedicated to the relaxation parameters (M₀, T₁ and T₂) of plants (especially sorghum) for different stress conditions. The underlying idea is to identify NMR parameters of the plant's health as suggested by Van As et al. (1985).

We aim to push the boundaries of very low magnetic field NMR by developing a highly homogenous resistive magnet while considering the constraint of self-heating, size reduction and versatility to keep the integrity of the plant under study. This constraint implies taking into account the thermal behavior. For this purpose, we describe an extension of the space harmonic suppression (SHS) method (Coillot et al., 2016), which allows us to enhance the magnetic field homogeneity of coils.

2 Magnetic field homogeneity of coils: problems and overview

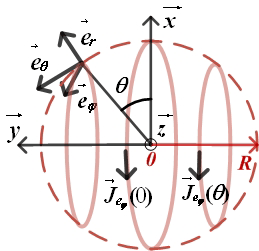
The condition that must be fulfilled by the current density to produce a homogenous magnetic field for spherical coils (demonstrated by Clarck, 1938; Everett and Osemeikhian, 1966), and known as “cosine” distribution, is expressed as

$$\begin{array}{}\text{(1)}& {\mathit{J}}_{{\mathit{e}}_{\mathit{\phi }}}\left(\mathit{\theta }\right)=J_{\mathrm{0}}\cos \left(\mathit{\theta }\right){\mathit{e}}_{\mathit{\phi }},\end{array}$$

where J₀ is the current density magnitude and θ is the angular position over a circle of radius R with respect to a reference axis (x; see Fig. 1).

An equivalent condition arises for the generation of a transverse homogenous magnetic field produced within a cylindrical volume. Numerous RF coils used in NMR spectroscopy and imaging take advantage of this condition (Bolinger et al., 1988; Coillot et al., 2007; Harpen, 1991; Hayes et al., 1985; Hoult and Richards, 1976; Mispelter et al., 2006). Note that, unlike superconducting magnets, the reverse current is not optimal in the presence of Joule's effect since the reverse current reduces the magnetic field strength, while it increases the power consumption.

The SHS method, reported in Coillot et al. (2016), consists in approaching the cosine current density distribution by calculating discrete conductors' angular positioning on a circle (see Fig. 1), aiming to approach cosine distribution by means of a Fourier series formalism. It was assumed that the same current is flowing in each conductor. The angle solutions which have been obtained for the two, four and six pairs of coils are mentioned here:

• SHS 2 (θ₁=30^∘, NB: this angle value is slightly different from the Helmholtz coil one: θ_Helm=26.57^∘, converse to what was erroneously written in Coillot et al. (2016);

• SHS 4 (θ₁=12^∘ et θ₂=48^∘);

• SHS 6 (θ₁=11.56^∘, θ₂=26^∘ and θ₃=56^∘).

Figure 1 Current density distribution of spherical coils oriented along e_φ in spherical coordinates.

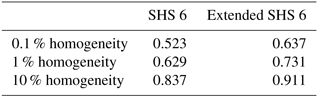
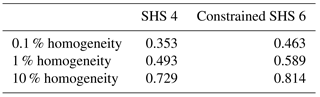
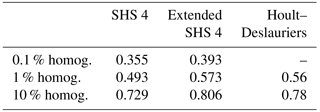
The efficiency of the method in designing highly homogenous coils is based on the evaluation of the homogeneity factor: the 0.1, 1 and 10 % homogeneities are defined as the fraction of the coil diameter where the magnetic field intensity remains, respectively, within 0.1, 1 and 10 % of its maximum value (Table 1).

Table 1 Axisymmetric coil homogeneity study: comparison between several coil configurations: Helmholtz, SHS 2, SHS 4 and SHS 6.

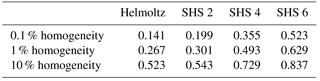
These results suggest that a homogeneity sufficient to perform quantitative NMR experiments and relaxometry (hundreds of ppm) in a wide volume fraction of the coil can be reached.

3 Extended SHS method

While the restriction of an equal current flowing into the conductors forming the coil is relevant for most of the MRI probes where the conductors are in series (a notable exception being the four-coil MRI probes proposed by Hoult and Deslauriers, 1990), it appears that this restriction is not required in many situations like calibration coils, but also for the coil producing the static magnetic field, which is the concern of a portable NMR device.

3.1 Current density distribution

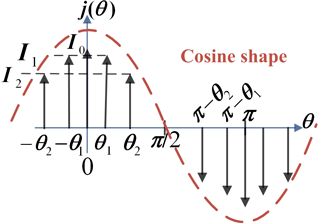
Thus, we will consider a more general current density distribution in coils: the current magnitude in a coil is independent of the ones in other coils (see Fig. 2). Then, by extending the method, the current density distribution (illustrated by Fig. 3) will be expressed as

$$\begin{array}{ll}{\displaystyle }j\left(\mathit{\theta }\right)=& {\displaystyle }{I}_{\mathrm{0}}\left(\mathit{\delta }\right(\mathit{\theta })-\mathit{\delta }(\mathit{\theta }-\mathit{\pi }\left)\right)+{\mathrm{\Sigma }}_{n=\mathrm{1}}^N{I}_n\left(\mathit{\delta }(\mathit{\theta }-{\mathit{\theta }}_n)\right.\\ \text{(2)}& {\displaystyle }& {\displaystyle }\left.+\mathit{\delta }(\mathit{\theta }+{\mathit{\theta }}_n)-\mathit{\delta }(\mathit{\theta }-{\mathit{\theta }}_n-\mathit{\pi })-\mathit{\delta }(\mathit{\theta }+{\mathit{\theta }}_n-\mathit{\pi })\right),\end{array}$$

where δ(θ) is the one-dimensional Dirac distribution as a function of the angle θ. Then, by applying a reasoning analog to the one developed in Coillot et al. (2016), the Fourier series coefficient (a_2k−1) of j(θ) can be calculated. The current density function (j(θ)) can then be re-written as a Fourier series:

$$\begin{array}{ll}{\displaystyle }j\left(\mathit{\theta }\right)=& {\displaystyle }{\mathrm{\Sigma }}_{k=\mathrm{1}}^{\mathrm{\infty }}\left({\mathrm{\Sigma }}_{n=\mathrm{1}}^N{\displaystyle \frac{\mathrm{2}}{\mathit{\pi }}}\left(I_{\mathrm{0}}+\mathrm{2}{I}_n\cos \left(\right(\mathrm{2}k-\mathrm{1}\left){\mathit{\theta }}_n\right)\right)\right)\\ \text{(3)}& {\displaystyle }& {\displaystyle }\times \cos \left((\mathrm{2}k-\mathrm{1})\mathit{\theta }\right).\end{array}$$

3.2 Magnetic field generation

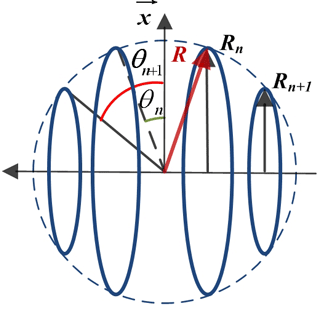
The magnetic field produced for the in planta portable NMR experiments requires the plant to be placed in the center of the coil. That leads us to focus only on the even SHS coils case (i.e., without a central coil; thus, the term I₀ vanishes) composed of N pairs of coils. Each coil has N_n conductors flown by a current I_n. The magnetic field generated at the center of the SHS coil pair (B_n), based on the magnetic field at the center of a symmetric pair of coils, can be expressed either as a function of the coil radius (R_n), see Eq. (4), or as a function of the radius supporting circle (R, such as in R_n=Rcos(θ_n)), defined in Fig. 2; see Eq. (5).

$$\begin{array}{}\text{(4)}& {\displaystyle }& {\displaystyle }{B}_n={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}}{R_n}}{N}_n{I}_n{\cos }^{\mathrm{3}}\left({\mathit{\theta }}_n\right),\text{(5)}& {\displaystyle }& {\displaystyle }{B}_n={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}}{R}}{N}_n{I}_n{\cos }^{\mathrm{2}}\left({\mathit{\theta }}_n\right).\end{array}$$

The total magnetic field (B_SHS) produced by the N pairs of coils results from the sum of the magnetic fields produced by each pair of coils:

$$\begin{array}{}\text{(6)}& B_{\mathrm{SHS}}={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}}{R}}{\mathrm{\Sigma }}_{n=\mathrm{1}}^N{N}_n{I}_n{\cos }^{\mathrm{2}}\left({\mathit{\theta }}_n\right).\end{array}$$

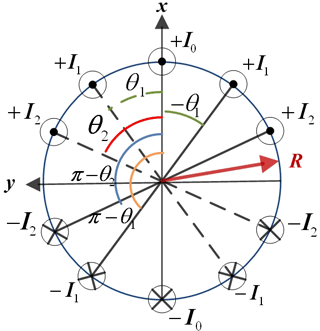
Figure 2 Electrical conductors of unknown angular positions (θ_n), flown by currents I_n, distributed along the circumference.

Figure 3 Illustration of the space current density distribution for non-identical currents flowing through the coils.

3.3 Formulation of the homogenous magnetic field coil design problem

In the context of N turn coil pairs without the central coil, we will have to determine the N angles and currents allowing us to produce the target magnetic field (B_SHS=8 mT in our design case) and satisfying the harmonic suppression. That gives us 2N equations allowing us to suppress (2N−1) harmonics. The first equation of the equation set (Eq. 7) allows the magnetic field goal to be reached (namely Eq. 6), while the other equations are deduced from harmonics suppression (Eq. 3):

$$\begin{array}{ll}{\displaystyle }& {\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}}{R}}{\mathrm{\Sigma }}_{n=\mathrm{1}}^N{N}_n{I}_n{\cos }^{\mathrm{2}}\left({\mathit{\theta }}_n\right)=B_{\mathrm{SHS}}\\ {\displaystyle }& {\displaystyle }{\mathrm{\Sigma }}_{n=\mathrm{1}}^N{I}_n\cos \left(\mathrm{3}{\mathit{\theta }}_n\right)=\mathrm{0}(k=\mathrm{2})\\ {\displaystyle }& {\displaystyle }\mathrm{\dots }\\ {\displaystyle }& {\displaystyle }{\mathrm{\Sigma }}_{n=\mathrm{1}}^N{I}_n\cos \left((\mathrm{2}j-\mathrm{1}){\mathit{\theta }}_n\right)=\mathrm{0}(k=j)\\ {\displaystyle }& {\displaystyle }\mathrm{\dots }\\ \text{(7)}& {\displaystyle }& {\displaystyle }{\mathrm{\Sigma }}_{n=\mathrm{1}}^N{I}_n\cos \left((\mathrm{4}N-\mathrm{1}){\mathit{\theta }}_n\right)=\mathrm{0}(k=\mathrm{2}N).\end{array}$$

This set of equations offers the possibility of designing the coil generating the required magnetic field and allowing us to enhance the homogeneity by means of the harmonics suppression technique.

3.4 Numerical resolution aspects

The angle solutions of Eq. (7) are obtained using a numerical resolution tool. Nevertheless, for a large number of variables, the algorithm may converge to an aberrant solution with some angles higher than π∕2, which satisfies the harmonic cancellation but does not maximize the magnetic field. Thus, it is recommended in such a case to solve the designed problem using optimization formalism. The objective function will be a compromise between the maximization of the magnetic field production g(u) (left member of the first equation of Eq. 7) and the minimization of function f(u), ensuring the cancellation of the harmonics (remaining equations of Eq. 7):

$$\begin{array}{ll}\text{(8)}& {\displaystyle }& {\displaystyle }g\left(u\right)={\left({\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}}{R}}{\mathrm{\Sigma }}_{n=\mathrm{1}}^N{N}_n{I}_n{\cos }^{\mathrm{2}}\left({\mathit{\theta }}_n\right)\right)}^{\mathrm{2}},{\displaystyle }& {\displaystyle }f\left(u\right)={\left({\mathrm{\Sigma }}_{n=\mathrm{1}}^N{I}_n\cos \left(\mathrm{3}{\mathit{\theta }}_n\right)\right)}^{\mathrm{2}}+\mathrm{\dots }\\ \text{(9)}& {\displaystyle }& {\displaystyle }+{\left({\mathrm{\Sigma }}_{n=\mathrm{1}}^N{I}_n\cos \left(\right(\mathrm{4}N-\mathrm{1}\left){\mathit{\theta }}_n\right)\right)}^{\mathrm{2}},\end{array}$$

where u is the set of variables (θ_n and I_n).

Next, the optimization formalism will permit us to limit the feasible space solution research using inequality constraints. Thus, an example of optimization formalism for the SHS coil design will be

$$\begin{array}{ll}\text{(10)}& {\displaystyle }Min\left(u\right)& {\displaystyle }\left[{\displaystyle \frac{\mathit{\alpha }}{g\left(u\right)}}+\mathit{\beta }f\left(u\right)\right],{\displaystyle }& {\displaystyle }\mathrm{0}<{\mathit{\theta }}_n<\mathit{\pi }/\mathrm{2},\\ {\displaystyle }& {\displaystyle }{I}_n>\mathrm{0}.\end{array}$$

α and β are weighting parameters permitting us to guide the optimization resolution according to the designer priorities. They also have the role of normalizing different goals. In our case, the harmonics suppression is the primary objective, so we choose a high value for the β parameter (β=1000), while the α is used to normalize the function ($\mathit{\alpha }={\mathit{\mu }}_{\mathrm{0}}/R$).

Lastly, the angle solutions of the optimization problem are obtained using a numerical optimization tool.

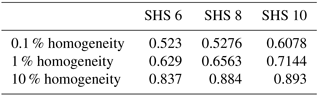
To conclude this section, we report the angle solutions (expressed in radians) and homogeneity efficiency (see Table 2) obtained for SHS 8 and SHS 10 by means of the optimization formalism of Eq. (10):

• SHS 8 (θ₁=0, θ₂=0.439, θ₃=0.609 and θ₄=1.061);

• SHS 10 (θ₁=0.163, θ₂=0.264, θ₃=0.573, θ₄=0.7901 and θ₅=1.159).

The optimization formalism opens the way to a flexible solution where other kinds of constraints can be implemented (given range of value for instance).

4 Extended SHS coil design

The magnetic field produced for the in planta portable NMR experiments results in a compromise between the generation of a homogenous magnetic field on the one side and self-heating to avoid heating stress of the plant on the other side (it is assumed that the local surrounding sorghum stem temperature increase should remain $<\mathrm{\Delta }T\left(K\right)=\mathrm{10}$ K). In our case, the choice of the intensity of magnetic field at 8 mT was based on a compromise between the SNR closed to the one demonstrated in pioneer work (Asfour, 2011) and the portability of the device in fields. The use of SHS coils allows us to seek the best compromise thanks to the splitting of the dissipated power over several coils. Lastly, the application requires access to the center of the coil and has led us to consider a constrained design option.

Table 2 Axisymmetric coil homogeneity study: comparison between several coil configurations: SHS 6, SHS 8 and SHS 10.

4.1 Extended SHS 4 design

We consider the case of two pairs of turns (i.e., N=2) with identical turn numbers (i.e., $N_{\mathrm{1}}=N_{\mathrm{2}}=N$). Thus, we have four variables: two angles and two currents, which allows us to cancel the first three spatial harmonics:

$$\begin{array}{ll}\text{(11)}& {\displaystyle }& {\displaystyle \frac{N{\mathit{\mu }}_{\mathrm{0}}}{R}}\left(I_{\mathrm{1}}{\cos }^{\mathrm{2}}\left({\mathit{\theta }}_{\mathrm{1}}\right)+I_{\mathrm{2}}{\cos }^{\mathrm{2}}\left({\mathit{\theta }}_{\mathrm{2}}\right)\right)=\mathrm{8}\mathrm{mT},{\displaystyle }& {\displaystyle }{I}_{\mathrm{1}}\cos \left(\mathrm{3}{\mathit{\theta }}_{\mathrm{1}}\right)+I_{\mathrm{2}}\cos \left(\mathrm{3}{\mathit{\theta }}_{\mathrm{2}}\right)=\mathrm{0},\\ {\displaystyle }& {\displaystyle }{I}_{\mathrm{1}}\cos \left(\mathrm{5}{\mathit{\theta }}_{\mathrm{1}}\right)+I_{\mathrm{2}}\cos \left(\mathrm{5}{\mathit{\theta }}_{\mathrm{2}}\right)=\mathrm{0},\\ {\displaystyle }& {\displaystyle }{I}_{\mathrm{1}}\cos \left(\mathrm{7}{\mathit{\theta }}_{\mathrm{1}}\right)+I_{\mathrm{2}}\cos \left(\mathrm{7}{\mathit{\theta }}_{\mathrm{2}}\right)=\mathrm{0}.\end{array}$$

The solution of this set of equations is obtained by means of a numerical minimization and leads to θ₁=0.3142, θ₂=0.9425, I₁=1.7794 A and I₂=1.0997 A ($I_{\mathrm{2}}/I\mathrm{1}=\mathrm{0.618}$), which is slightly different from the solution obtained by Hoult and Deslauriers's coil (cf. Hoult and Deslauriers, 1990) mentioned here (${\mathit{\psi }}^{\prime }=\mathit{\pi }/\mathrm{2}-\mathit{\psi }=\mathrm{0.288}\approx {\mathit{\theta }}_{\mathrm{1}}$, ${\mathit{ϵ}}^{\prime }=\mathit{\pi }/\mathrm{2}-\mathit{ϵ}=\mathrm{0.871}\approx {\mathit{\theta }}_{\mathrm{2}}$ and $I_{\mathrm{2}}/I\mathrm{1}=\mathrm{0.682}$).

Finally, we report, in Table 3, the comparison of the 1 % magnetic field homogeneity for standard SHS, an extended SHS coil and Hoult–Deslauriers coils.

4.2 Extended SHS 6 design

We now consider the case of three pairs of turns (i.e., N=3). We have six variables: three angles and three currents, which allows us to cancel five harmonics:

$$\begin{array}{ll}\text{(12)}& {\displaystyle }& {\displaystyle \frac{N{\mathit{\mu }}_{\mathrm{0}}}{R}}\left(I_{\mathrm{1}}{\cos }^{\mathrm{2}}\left({\mathit{\theta }}_{\mathrm{1}}\right)+I_{\mathrm{2}}{\cos }^{\mathrm{2}}\left({\mathit{\theta }}_{\mathrm{2}}\right)+I_{\mathrm{3}}{\cos }^{\mathrm{2}}\left({\mathit{\theta }}_{\mathrm{3}}\right)\right)=\mathrm{8}\mathrm{mT},{\displaystyle }& {\displaystyle }{I}_{\mathrm{1}}\cos \left(\mathrm{3}{\mathit{\theta }}_{\mathrm{1}}\right)+I_{\mathrm{2}}\cos \left(\mathrm{3}{\mathit{\theta }}_{\mathrm{2}}\right)+I_{\mathrm{3}}\cos \left(\mathrm{3}{\mathit{\theta }}_{\mathrm{3}}\right)=\mathrm{0},\\ {\displaystyle }& {\displaystyle }{I}_{\mathrm{1}}\cos \left(\mathrm{5}{\mathit{\theta }}_{\mathrm{1}}\right)+I_{\mathrm{2}}\cos \left(\mathrm{5}{\mathit{\theta }}_{\mathrm{2}}\right)+I_{\mathrm{3}}\cos \left(\mathrm{5}{\mathit{\theta }}_{\mathrm{3}}\right)=\mathrm{0},\\ {\displaystyle }& {\displaystyle }{I}_{\mathrm{1}}\cos \left(\mathrm{7}{\mathit{\theta }}_{\mathrm{1}}\right)+I_{\mathrm{2}}\cos \left(\mathrm{7}{\mathit{\theta }}_{\mathrm{2}}\right)+I_{\mathrm{3}}\cos \left(\mathrm{7}{\mathit{\theta }}_{\mathrm{3}}\right)=\mathrm{0},\\ {\displaystyle }& {\displaystyle }{I}_{\mathrm{1}}\cos \left(\mathrm{9}{\mathit{\theta }}_{\mathrm{1}}\right)+I_{\mathrm{2}}\cos \left(\mathrm{9}{\mathit{\theta }}_{\mathrm{2}}\right)+I_{\mathrm{3}}\cos \left(\mathrm{9}{\mathit{\theta }}_{\mathrm{3}}\right)=\mathrm{0},\\ {\displaystyle }& {\displaystyle }{I}_{\mathrm{1}}\cos \left(\mathrm{11}{\mathit{\theta }}_{\mathrm{1}}\right)+I_{\mathrm{2}}\cos \left(\mathrm{11}{\mathit{\theta }}_{\mathrm{2}}\right)+I_{\mathrm{3}}\cos \left(\mathrm{11}{\mathit{\theta }}_{\mathrm{3}}\right)=\mathrm{0}.\end{array}$$

The solution of this set of equations is obtained by means of a numerical minimization and leads to θ₁=0.2244, θ₂=0.6732, θ₃=1.122, I₁=1.305 A, I₂=1.0465 A and I₃=0.5808 A, while the homogeneity efficiency is reported in Table 4.

Table 3 Four-turn axisymmetric coil homogeneity: comparison between the four-turn SHS coils, the four-turn extended SHS and the four-turn Hoult and Deslauriers coil.

The results of the simulations show that the extended SHS method makes it possible to improve the homogeneity in the region where the NMR measurement was achieved.

4.3 Thermal behavior of SHS coils

Splitting of SHS coils into multiple coils has an important advantage, with respect to the thermal behavior, since it allows us to split the total power on multiple coils (or, in other words, to increase the exchange area of coils). The thermal behavior will be studied with a special focus for the inner coil, which is the closest to the plant stem where the self-heating must be limited. The thermal exchange between neighbor coils is neglected.

4.3.1 Power to be dissipated by SHS coils

The power dissipated by Joule's effect for the nth coil (with resistance Res_n), see Fig. 4, is expressed as

$$\begin{array}{}\text{(13)}& P_n={\mathrm{Res}}_n{I}_n^{\mathrm{2}},\end{array}$$

where I_n is the current flowing through the nth coil and Res_n is its resistance, given by the following equation:

$$\begin{array}{}\text{(14)}& {\mathrm{Res}}_n=\mathrm{2}\mathit{\rho }{\displaystyle \frac{N_n\times R\times \cos \left({\mathit{\theta }}_n\right)}{r_{\mathrm{c}}^{\mathrm{2}}}},\end{array}$$

where ρ is the material resistivity, r_c is the wire radius and N_n is the number of turns of the considered nth coil.

Table 4 Six-turn axisymmetric coil homogeneity: comparison between the six-turn SHS coils and the six-turn extended SHS.

4.3.2 Thermal model

The thermal resistance of the coil will be neglected since a copper conductor is assumed. Next, the power to be dissipated (P_n) will be evacuated by means of natural convection (an average convection coefficient h will be assumed) and radiation through the exchange area of the coil (S_n):

$$\begin{array}{}\text{(15)}& P_n=h{S}_n\left(T_{\mathrm{s}}-T_{\mathrm{\infty }}\right)+\mathit{\sigma }\mathit{ϵ}{S}_n\left(T_{\mathrm{s}}^{\mathrm{4}}-T_{\mathrm{\infty }}^{\mathrm{4}}\right),\end{array}$$

where T_s is the average surface temperature, σ is the Stefan–Boltzmann constant (5.6703e⁻⁸ Wm⁻² K⁻⁴), ϵ is the emissivity of the surface of a material (a black body is assumed, i.e., ϵ=1) and T_∞ is the ambient temperature.

Figure 4 SHS coil constituted of N pairs of coils.

The natural convection coefficient is preliminarily determined by fitting the thermal prediction given by Eq. (15) with thermal measurement on a SHS 4 prototype (whose geometrical parameters are summarized in Table 5 below), supplied with $I_{\mathrm{1}}=I_{\mathrm{2}}=\mathrm{1.4}$ A (in order to produce 8 mT). Consequently the measured temperature of the coil overheating, ΔT<25 K and T_∞=297 K, leads us to estimate h=6 Wm⁻² K⁻¹.

4.3.3 Thermal behavior of extended SHS 6

We consider the case of the extended SHS 6 whose angles and currents are given in Sect. 4.2, while parameters for the inner coil are summarized in Table 6. The model of Eq. (15) permits us to estimate the surface temperature of inner coil overheating: ΔT<25 K. Thus, it appears that the extended SHS 6 reduces the temperature, but not sufficiently so to make the coil compliant with the plant environment.

4.4 Constrained extended SHS 6: fixed current and aperture angle θ₁

To solve the thermal issue we will now constrain the formulation of the extended SHS by fixing some parameters like the current intensity flowing into the inner coil (1 A should permit us to limit the coil overheating: ΔT<10 K) and the angle of the central pair of coils (in order to have a sufficient gap to insert the plant stem, namely ≃30 mm). Thus, we will fix I₁=1 A and θ₁=0.2244, which reduces our number of variables to four and thus simplifies the set of Eq. (12). The solutions obtained for the new set of equations are θ₁=0.2244, θ₂=0.4509, θ₃=0.9676, I₁=1 A, I₂=0.8844 A and I₃=1.0017 A.

Table 5 Geometric parameters of SHS 4 (supplied with $I_{\mathrm{1}}=I_{\mathrm{2}}=\mathrm{1.4}$ A).

Table 6 Homogeneity comparison between the SHS 4 prototype and the constrained extended SHS 6.

5 Experimental results

5.1 SHS 4 coils prototype

As depicted before, the SHS 4 coil could suffer from too much overheating. In order to solve this issue we increased the exchange area (S=0.24 m²) and the nature of material support so as to reduce the temperature. Our goal is to evacuate heat by the natural convection mechanism, so we created a simple heat sink placed around the element to be cooled (coils). To make it, we have chosen a non-magnetic aluminum material with a high thermal conductivity and a black paint to get the emissivity coefficient as close as possible to 1. The improved setup (Fig. 5) exhibits an overheating of about ≃ 12 K, which satisfies the plant integrity.

Our prototype allowed us to measure, with a one-pulse NMR sequence (acquisition time < 3 mn for repetition time about 1 s), the signal at the stem of a sorghum plant directly in the greenhouse (Fig. 6).

The NMR signal of plants measured at 333 kHz (which corresponds to the expected Larmor frequency of ¹H at 8 mT) demonstrates clearly the homogeneity performance: the line width of the NMR signal used to estimate the homogeneity of the prototype is about 900 ppm (300 Hz) in a volume of 4 cm³ corresponding to the internal volume of the clipping RF coil dedicated to the plant stem (diameter = 20 mm and height = 14 mm).

Note that the NMR system comprises a resistive SHS magnet (without gradient coils) flowing by current produced by an enslaved power supply, a homemade coil dedicated to sorghum plants, an amplifier low noise high impedance as suggested in Asfour (2011) and concerning the pulse sequencer, a Chameleon (RS2D Company) was used.

Figure 5 Portable NMR prototype based on the SHS 4 model at 333 kHz for agronomic studies (R=100 mm, N_n=320, window of wire winding: 18 mm × 15 layers, r_c=0.4 mm, and the prototype total weight = 7 kg).

From a practical point of view, it is helpful to improve the homogeneity of the magnetic field starting from identical currents calculated by the SHS method and finally adjusting them by fine changes. This allows, when we are in good experimental conditions, to reach a homogeneity as low as 600 ppm (see Fig. 6).

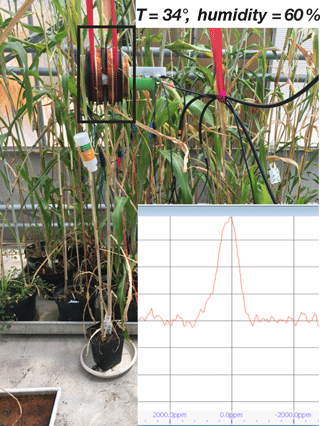
Figure 6 NMR spectrum of a sorghum plant at 333 kHz by the SHS 4 coils prototype in a greenhouse at CIRAD.

The numerical computation of the homogeneity for the SHS 4 coil obtained by means of the standard deviation extracted from the magnetic field distribution over the centered sphere (performed with a numerical finite-element software) gives a linewidth value of about 456 ppm, which is in good agreement with the experimental one.

5.2 Constrained extended SHS 6 coils prototype

The design validated on the SHS 4 prototype results has encouraged us to go further in the prototype construction. The design of the constrained extended SHS 6 (based on parameters given in Sect. 4.4) seems to offer a promising compromise between homogeneity, weight, overheating and accessibility to the plant stem.

Indeed, increasing the number of coils to produce the same magnetic field is known to be beneficial for the thermal behavior.

The gap is now 30 mm (all the coils of the prototype have the same number of turns equal to 320 turns) and totally compliant with our future experiments.

The constrained SHS 6 prototype (as shown in Fig. 7) nominally supplied has exhibited an overheating limited to about ≃ 6 K around the sorghum stem under test, which is within the acceptable overheating range.

Our prototype allowed us also to measure with a one-pulse NMR sequence (acquisition time < 3 mn for repetition time about 1 s) the signal at the stem of a sorghum plant directly in the greenhouse. The homogeneity of the prototype is improved at 333 kHz (8 mT) by 10 % compared to the prototype SHS 4, but it would be even better if we had not imposed the gap restriction.

6 Conclusion

The extended SHS method has been demonstrated to be an efficient and intuitive analytic tool to determine the conductor distribution enhancing the coil homogeneity.

Figure 7 Portable NMR prototype based on a constrained SHS 6 model at 333 kHz for agronomic studies (R=100 mm, N_n=320, window of wire winding: 18mm mm × 15 layers, r_c=0.4 mm and the prototype total weight = 10 kg).

The simplicity of the formulation allows us to make a more flexible design, as shown on the portable NMR prototype. Only one angle could be fixed for practical reasons, like a geometrical aperture, while the other angles and currents could be computed to preserve a high homogeneity.

The combination of this method (allowing us to predict the overheating of the coil) with the thermal model has been successfully used to design and build a homogenous coil which keeps plant integrity. This opens the way for outdoor agronomic studies using this device, the only remaining concern the power supply management. At present, we are investigating modifications of NMR relaxation parameters (M₀, T₁ and T₂) during the dynamic diurnal cycle in normal and abiotic stress conditions.