Non-destructive testing of arbitrarily shaped refractive objects with millimetre-wave synthetic aperture radar imaging

Millimetre-wave (mmW) imaging is an emerging technique for non-destructive testing. Since many polymers are transparent in this frequency range, mmW imaging is an attractive means in the testing of polymer devices, and images of relatively high resolution are possible. This contribution presents an algorithm for the precise imaging of arbitrarily shaped dielectric objects. The reconstruction algorithm is capable of automatically detecting the object's contour, followed by a material-sensitive reconstruction of the object's interior. As an example we examined a polyethylene device with simulated material defects, which could be depicted precisely.

1 Introduction

Throughout the whole process chain, quality management is a fundamental task in industrial production. The monitoring of devices and materials is a core issue in order to guarantee a consistent quality of the products. For the detection of material defects the interior of devices is of essential interest. When the device under test (DUT) is not transparent to the human eye, wave-based imaging, employing electromagnetic (EM) or acoustic waves, can be applied. There is a variety of wave-based techniques utilized for non-destructive testing (NDT). Among them are microwave and terahertz radar, ultrasound, X-ray tomography and many more.

In this contribution we present an imaging system employing millimetre waves. Millimetre waves have become an emerging technique in recent years. Due to miniaturization advances in semiconductor technology, leading to considerable cost reduction, they have become attractive for a huge field of applications ranging from NDT to security screening and others (Ahmed et al., 2012; Agarwal et al., 2015). They offer a number of specific advantages compared to the other techniques named above: though they cannot provide the resolution of X-ray, they have the advantage of a non-ionizing radiation. Furthermore, mmW imaging is less costly than employing EM waves of higher frequencies (e.g. X-ray or Terahertz). Sound- or ultrasound-based imaging on the other hand is a cost-efficient solution for many NDT applications. However, it usually requires the DUT to be immersed in water or another coupling medium – for air-coupled ultrasound typically is not able to properly penetrate into the inside of solids due to the very high difference in the acoustic impedances (Hillger et al., 2015).

From their frequency range and the corresponding wavelengths, millimetre waves offer a good compromise between penetration depth and resolution. The resolution, both laterally and in the range direction, lies in the range of a few millimetres, depending on system parameters like bandwidth or aperture size, but also on the DUT's material (Ahmed et al., 2012).

For the data acquisition a synthetic aperture radar (SAR) is utilized. The SAR technique originates from remote sensing – therefore SAR processing algorithms originally were based on the assumption of a free-space propagation of the electromagnetic wave. This assumption still holds when screening dielectric devices which exhibit a relative electrical permittivity equal (or very close) to one. However, when applying such algorithms to a scenario in which the wave propagates through a material with a refractive index significantly greater than one, the reconstruction is based on false assumptions and the reconstructed image will be of low quality or even faulty. The reasons for this are the change in phase velocity and the resulting refraction of the wave occurring at the material boundary in the case of non-normal incidence.

The reconstruction algorithm presented in this paper takes into account the effects named above. It can therefore be applied not only to surroundings that exhibit a free-space-like behaviour, but also to subsurface imaging of refractive materials, which includes many polymers, too.

The article is outlined as follows: first a brief review of the theory of electromagnetic wave propagation in heterogeneous media will be given. Then, the image formation concept will be presented. Starting from the automated detection of the DUT's surface, two approaches for the handling of the material inhomogeneity are shown. The concept was evaluated by measurements – the results are presented in Sect. 4. Eventually a conclusion will sum up the main issues of the article.

2 Theory

The propagation of an electromagnetic wave can be described by the Helmholtz equation for the electric field strength in the time domain E(t):

$$\begin{array}{}\text{(1)}& {\mathrm{\nabla }}^{\mathrm{2}}\mathit{E}\left(t\right)-c{\displaystyle \frac{{\partial }^{\mathrm{2}}}{\partial t^{\mathrm{2}}}}\mathit{E}\left(t\right)=\mathrm{0},\end{array}$$

and analogously for the magnetic field. Equation (1) is a homogeneous wave equation, with c denoting the wave's propagation velocity. One possible solution of the partial differential equation Eq. (1) is a plane wave. Assuming the wave to propagate in a direction x, then the plane wave equation reads as

$$\begin{array}{}\text{(2)}& E\left(x,t\right)=\mathrm{|}E\mathrm{|}\cdot \exp \left[j\left(\mathit{\omega }t-kx\right)\right].\end{array}$$

Here, j is the imaginary unit, ω is the angular frequency and k is the wavenumber, related to the wavelength λ by

$$\begin{array}{}\text{(3)}& k={\displaystyle \frac{\mathrm{2}\mathit{\pi }}{\mathit{\lambda }}}.\end{array}$$

The phase velocity c is

$$\begin{array}{}\text{(4)}& c={\displaystyle \frac{\mathit{\omega }}{k}}={\displaystyle \frac{\mathrm{1}}{\sqrt{\mathit{\mu }\mathit{\epsilon }}}}={\displaystyle \frac{\mathrm{1}}{\sqrt{{\mathit{\mu }}_{\mathrm{0}}{\mathit{\mu }}_{\mathrm{r}}{\mathit{\epsilon }}_{\mathrm{0}}{\mathit{\epsilon }}_{\mathrm{r}}}}},\end{array}$$

depending on the material's parameters μ_r and ε_r (relative magnetic permeability and relative electric permittivity, respectively). The parameters μ₀ and ε₀ in Eq. (4) denote the magnetic permeability and electric permittivity of a vacuum. When considering only non-magnetic materials as is done here, the phase velocity in a material is

$$\begin{array}{}\text{(5)}& c={\displaystyle \frac{c_{\mathrm{0}}}{\sqrt{{\mathit{\epsilon }}_{\mathrm{r}}}}}={\displaystyle \frac{c_{\mathrm{0}}}{n}},\end{array}$$

where c₀ is the speed of light in a vacuum and n is the refractive index of the material. When passing through a boundary between two materials of different refractive indices n₁ and n₂, an EM wave will be refracted according to Snell's law,

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{\sin \left(\mathit{\alpha }\right)}{\sin \left(\mathit{\beta }\right)}}={\displaystyle \frac{n_{\mathrm{2}}}{n_{\mathrm{1}}}},\end{array}$$

where α denotes the angle of incidence and β the angle of refraction.

Snell's law can be derived from Fermat's principle (Hecht, 2002). Both Snell's law and Fermat's principle and their notations originate from optics, but can be applied to electromagnetic waves of other frequency ranges, too.

Fermat's principle states that a wave travelling from a point P₁ to another point P₂ will follow that optical path whose optical length is shorter than the optical length of any other path in a certain neighbourhood to it (Born and Wolf, 1980). The optical path length (opl) is the geometrical length s multiplied by the refractive index n(x, y, z) of the respective surrounding:

$$\begin{array}{}\text{(7)}& \mathrm{opl}=\underset{P_{\mathrm{1}}}{\overset{P_{\mathrm{2}}}{\int }}n(x,y,z)\mathrm{d}s.\end{array}$$

Consequently, the optical path taken between two points in space will minimize the functional Eq. (7). Since the optical length is

$$\begin{array}{}\text{(8)}& \mathrm{opl}=\underset{P_{\mathrm{1}}}{\overset{P_{\mathrm{2}}}{\int }}n\mathrm{d}s=c\cdot \underset{P_{\mathrm{1}}}{\overset{P_{\mathrm{2}}}{\int }}\mathrm{d}t,\end{array}$$

it follows that the time it takes the wave to traverse the way between P₁ and P₂ will be minimal – or more generally, stationary – also (Born and Wolf, 1980). Therefore, Fermat's principle is also known as the “principle of least time”.

3 Image reconstruction approach

3.1 General aspects on synthetic aperture imaging of heterogeneous media

Since synthetic aperture (SA) data are time- and space-dependent, the data processing can operate in the time and space domain or in the temporal and spatial frequency domain, which is obtained from a multidimensional Fourier transform of the measured data. A straightforward way to compress the SA data is by employing matched filtering in the time–space domain (Cumming and Wong, 2005). Here, for each pixel, that is, each possible target ${\mathit{r}}_{\mathrm{T},i}=$ (x_T,i, y_T,i, z_T,i)^T, a signal hypothesis is stated. This hypothesis equals the signal which the antenna at position ${\mathit{r}}_{\mathrm{A},j}=$ (x_A,j, y_A,j, z_A,j)^T would receive if there was a point scatterer located in the point r_T,i. In a next step, the hypotheses $s_{\mathrm{R}x,\mathrm{hyp},ij}\left({\mathit{r}}_{\mathrm{T},i},{\mathit{r}}_{\mathrm{A},j},f,t\right)$ are correlated with the actually measured signal $s_{\mathrm{R}x,\mathrm{meas},j}\left({\mathit{r}}_{\mathrm{A},j},f,t\right)$ at the current antenna position.

$$\begin{array}{ll}{\displaystyle }{\mathit{\psi }}_{ij}=& {\displaystyle }\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{s}_{\mathrm{R}x,\mathrm{hyp},ij}\left({\mathit{r}}_{\mathrm{T},i},{\mathit{r}}_{\mathrm{A},j},f,t+\mathit{\eta }\right)\\ \text{(9)}& {\displaystyle }& {\displaystyle }\cdot s_{\mathrm{R}x,\mathrm{meas},j}^{\ast }\left({\mathit{r}}_{\mathrm{A},j},f,t\right)\mathrm{d}t\end{array}$$

Here, η denotes the shift of the correlation integral. Those points in which a scattering truly occurs will then exhibit a high value for the correlation. All other points will exhibit a low value. Finally, in each voxel the values of the correlation function ψ_ij for all N_A antenna positions r_A,j, jϵ[1,N_A] and, in the case of a multi-frequency system, all N_f frequency steps f_m, mϵ[1,N_f], are summed up:

$$\begin{array}{}\text{(10)}& {\displaystyle }{\mathit{\psi }}_{\mathrm{sum},i}=\left|\sum _{j=\mathrm{1}}^{N_{\mathrm{A}}}\sum _{m=\mathrm{1}}^{N_{\mathrm{f}}}{\mathit{\psi }}_{ij}\right|.\end{array}$$

The resulting absolute value of the complex phasor ψ_sum,i is a measure of the probability that a point scatterer will be located in the respective point r_T,i. Converting the resulting absolute values of all N_T voxels r_T,i, iϵ[1,N_T] to brightness values returns the reconstructed image. That way, due to the pixel-wise filtering a precise compression of the targets can be obtained. However, it is obvious that this approach performs poorly in terms of computing time. This is especially true in the field of subsurface imaging: for the matched filtering, the path traversed by the wave needs to be known. In a heterogeneous surrounding, the wave will be refracted according to Eq. (6). However, the two angles α and β are not known a priori due to the unfocused antennas used for SAR. Therefore, the algorithm first has to determine the wave's path and then can proceed to the correlation procedure described above.

There is a number of reconstruction algorithms employed for SAR processing, like range-Doppler, chirp scaling or ω-k, which operate partly or entirely in the frequency domain (Cumming and Wong, 2005). In their original form they were based on the assumption of free-space propagation of the waves, but they have been adapted to inhomogeneous surroundings in past years (Albakhali and Moghaddam, 2009; Skjelvareid et al., 2011). However, in most cases the adapted algorithms can only handle planar objects. Some methods have been proposed which are also suitable for non-planar objects (Qin et al., 2014), but they require iterative processing steps, which considerably reduces their efficiency.

Therefore, matched filtering, which can be applied to any geometry, is still the most commonly used technique for subsurface imaging of irregularly shaped objects and will be used in this contribution, too.

3.2 Contour detection

If the contour of the object, which is the material boundary between the two media, is not known – or if it is known but its orientation towards the aperture plane is not – then the material boundary must be determined prior to the actual reconstruction. In the following, a way to extract the contour directly from the measurement data is shown.

Therefore, we first reconstruct the space between the aperture and the boundary. Here we can assume a free-space propagation of the EM wave, which means that no refraction has to be taken into account. The resulting image will be defocused, but the boundary will be reconstructed at its true position. Since the boundary will be the strongest reflection in most cases, one way to extract it directly is to search for the brightest pixel in each column. This approach is often used in ground-penetrating radar (Walker and Bell, 2001; Feng et al., 2010). It is convenient because it does not require additional measurements and there are effective algorithms existing for a free-space reconstruction.

Evidently however the error made in estimating the boundary will affect the quality (i.e. the signal-to-noise ratio, SNR) of the further reconstruction: due to the imaging principle of interfering single measurements it is essential that the resulting phase error caused by the estimation uncertainty is less than ±90^∘ in order to avoid destructive interference.

3.3 Refraction ray tracing

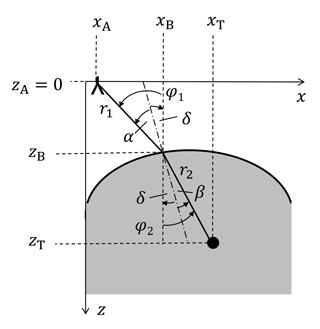
This section addresses the matched filtering for heterogeneous surroundings. A model of the scenario with the applied nomenclature is shown in Fig. 1. Here, the indices A, T, and B denote the coordinates of the respective antenna, boundary point and target. For clarity the indices i, j and m utilized in Sect. 3.1 are left out. The lateral (azimuth) direction is x; the range direction is z. For the sake of simplicity, all considerations are derived for a 2-D set-up.

We use a monostatic synthetic aperture radar, transmitting a signal s_Tx(tf). The receiver signal s_Rx(tf) is the wave backscattered from the DUT. The antenna positions spanning the synthetic aperture are equidistantly spaced and they are located at z=0. The antenna itself is modelled as an isotropic radiator. It is presumed that the volume to be reconstructed is located in the antenna's far-field. Then, the spherical wave radiated from the antenna will intersect with the object only at a small section of the sphere. This small section can be approximated as a quasi-plane phase front. Therefore, we model the incident wave to be a plane wave.

Figure 1 Model and nomenclature.

According to the antenna's isotropic directivity pattern, some part of the radiated electromagnetic field will be radiated in such a way that after traversing medium one and being refracted at the boundary it will actually meet the target (r₁ and r₂ in Fig. 1). Assuming isotropic scattering, some part of the reflected field will traverse the same way back to the antenna. Then, the received signal's phase will be

$$\begin{array}{}\text{(11)}& {\mathit{\phi }}_{\mathrm{R}x,\mathrm{hyp}}=\mathit{\omega }\cdot \mathrm{2}\cdot {\displaystyle \frac{r_{\mathrm{1}}+r_{\mathrm{2}}\sqrt{{\mathit{\epsilon }}_{\mathrm{r}\mathrm{2}}}}{c_{\mathrm{0}}}},\end{array}$$

which follows from Eqs. (2) to (5).

In Eq. (11), any phase offset due to the scatterer's reflection properties will be neglected, for it is a constant and thus will not influence the reconstruction process. Furthermore, since the reconstruction method will only evaluate the phase, the signal's amplitude is not considered further. Accordingly, the signal hypothesis becomes

$$\begin{array}{}\text{(12)}& s_{\mathrm{R}x,\mathrm{hyp}}=\mathrm{1}\cdot \exp \left(-j{\mathit{\phi }}_{\mathrm{R}x}\right)\end{array}$$

when setting the amplitude to a virtual value of one and inserting Eq. (11) for the phase.

Throughout this article we assume the object under test to consist of one non-magnetic, dielectric, frequency-independent and lossless material whose electric permittivity is known. For many NDT applications these are valid assumptions.

In the following, two means of finding the optical path in a two-media system are described. One is based on Snell's law, and the other one is based on Fermat's principle.

3.3.1 Ray tracing based on Fermat's principle

In order to determine the optical path, we search for that point within the boundary which is the true point of transit between the two media. Therefore, we discretize the boundary into a distribution of points. Then, the resulting optical path lengths from the antenna to the assumed target are a function of the boundary distribution z_B(x_B):

$$\begin{array}{}\text{(13)}& {\mathrm{opl}}_{\mathrm{1}}=\sqrt{{\left(x_{\mathrm{B}}-x_{\mathrm{A}}\right)}^{\mathrm{2}}+{\left(z_{\mathrm{B}}\right)}^{\mathrm{2}}}\end{array}$$

and

$$\begin{array}{}\text{(14)}& {\mathrm{opl}}_{\mathrm{2}}=\sqrt{{\left(x_{\mathrm{T}}-x_{\mathrm{B}}\right)}^{\mathrm{2}}+{\left(z_{\mathrm{T}}-z_{\mathrm{B}}\right)}^{\mathrm{2}}}\cdot \sqrt{{\mathit{\epsilon }}_{r\mathrm{2}}};\end{array}$$

see Fig. 1. The overall time it takes the wave to travel from the antenna to the target and back then follows as

$$\begin{array}{}\text{(15)}& \mathit{\tau }=\mathrm{2}\cdot {\displaystyle \frac{{\mathrm{opl}}_{\mathrm{1}}+{\mathrm{opl}}_{\mathrm{2}}}{c_{\mathrm{0}}}}.\end{array}$$

In order to determine the true path taken by the wave, the minimum of Eq. (15) has to be found. That boundary point (x_B, z_B) which minimizes Eq. (15) is the true point of transit between the two materials. The received phase then can be written as

$$\begin{array}{}\text{(16)}& {\mathit{\phi }}_{\mathrm{R}x}=\mathit{\omega }\mathit{\tau }\end{array}$$

and the signal hypothesis is obtained from Eq. (12).

Note that in order to improve the efficiency of this ray tracing, it is sufficient to consider only those boundary points which lie between the respective antenna and target positions. It is obvious that boundary points lying beyond cannot minimize the optical path.

3.3.2 Ray tracing based on Snell's law

Like before, we discretize the boundary into a distribution of points. From the geometry in Fig. 1 it can be seen that the incident angle is

$$\begin{array}{}\text{(17)}& \mathit{\alpha }={\tan }^{-\mathrm{1}}\left({\displaystyle \frac{x_{\mathrm{B}}-x_{\mathrm{A}}}{z_{\mathrm{B}}}}\right)+\mathit{\delta }.\end{array}$$

Herein, δ is the difference angle between the vertical and the normal in the respective point (x_B|z_B).

Likewise, for β we can write

$$\begin{array}{}\text{(18)}& \mathit{\beta }={\tan }^{-\mathrm{1}}\left({\displaystyle \frac{x_{\mathrm{T}}-x_{\mathrm{B}}}{z_{\mathrm{T}}-z_{\mathrm{B}}}}\right)+\mathit{\delta }.\end{array}$$

Additionally, α and β also have to fulfill the law of refraction, Eq. (6). That point of the boundary (x_B|z_B) which fits Eqs. (6), (17) and (18) is the true point of refraction. From it the lengths r₁ and r₂ are easily found by the Pythagorean theorem:

$$\begin{array}{}\text{(19)}& r_{\mathrm{1}}=\sqrt{{\left(x_{\mathrm{B}}-x_{\mathrm{A}}\right)}^{\mathrm{2}}+z_{\mathrm{B}}^{\mathrm{2}}}\end{array}$$

and

$$\begin{array}{}\text{(20)}& r_{\mathrm{2}}=\sqrt{{\left(x_{\mathrm{T}}-x_{\mathrm{B}}\right)}^{\mathrm{2}}+{\left(z_{\mathrm{T}}-z_{\mathrm{B}}\right)}^{\mathrm{2}}}.\end{array}$$

Having determined r₁ and r₂, the signal hypothesis follows from Eqs. (11) and (12).

Note that, of course, this approach is also applicable to a scenario with a planar material boundary. Then, in Eqs. (17) and (18) the difference angle δ can be set to zero.

Again, it is sufficient to consider only those boundary points between the current antenna position and target.

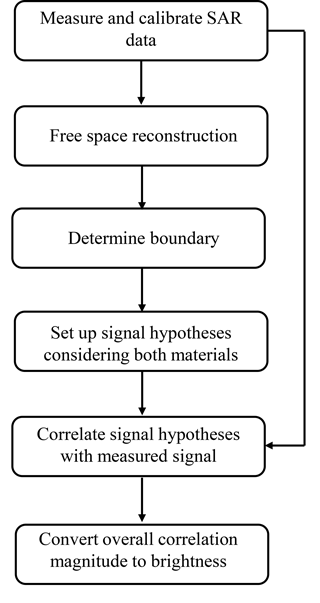
To sum up the concept, a flowchart of the complete image reconstruction procedure is shown in Fig. 2.

4 Experimental verification

4.1 Measurement set-up

Measurements were conducted to demonstrate the algorithm's feasibility. Here, we examined a polyethylene (PE) object into which two holes were drilled. Polyethylene displays a relative permittivity of ε_r = 2.3 in the relevant frequency range (Elvers, 2016). The drill holes represent air inclusions within the material. Such imperfections can be caused in the production process of the polymer or in the operation of a component.

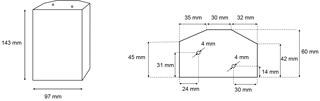
The object under test is depicted in Fig. 3. It was constructed to be invariant along the vertical direction, thus allowing for a 2-D reconstruction. Its surface was chosen to be non-planar and non-symmetric in order to demonstrate the algorithm's capacity to reconstruct rather complex objects.

Figure 2 Flowchart of the image reconstruction process.

Figure 3 Sketch of the object under test and its cross section with all relevant measures.

Figure 4 Employed measurement set-up. (a) Set-up sketch; (b) photograph of the measuring unit with an enlarged sketch of one of the antennas (Gumbmann, 2011).

Table 1 Measurement parameters.

The employed measurement set-up is shown in Fig. 4. It consists of one horizontal and two vertical traversing units, on which a pair of antennas is mounted. The traversing units allow for a movement along a distance of approximately 1.1 m in the vertical direction and 0.65 m in the horizontal direction. It is therefore possible to span a synthetic aperture of those dimensions. The two vertical units can be moved separately, which also makes multistatic measurements possible. For the measurements presented in this paper we employed a quasi-monostatic set-up, i.e. transmitter and receiver antenna were in close proximity; they were mounted with a spacing of 2 mm between them. The antennas were two H-polarized horn antennas with a physical aperture of 2.45 mm × 4 mm (see Fig. 4). The transmitted signal was generated by a vector network analyser (Agilent PNA E8363B) with frequency extenders (Oleson Microwave Labs V10VNA2-T/R). A 201-point SFCW signal covering the complete W-band (frequency range: $f_{min}=\mathrm{75}$ GHz to $f_{max}=\mathrm{110}$ GHz) was employed. Accordingly, the corresponding free-space wavelengths cover a range from λ_min = 2.7 mm to λ_max = 4 mm and a bandwidth of B = 35 GHz can be used. This bandwidth and wavelengths allow for a resolution in the range of a few millimetres, as will be discussed in Sect. 4.2. The radiated power was P_Tx = −17 dBm (20 µW).

In order to generate a 2-D image, a line aperture is sufficient. From the spatial sampling theorem the spacing between the antenna array positions must not exceed

$$\begin{array}{}\text{(21)}& \mathrm{\Delta }{d}_{max}={\mathit{\lambda }}_{min}/\mathrm{2}\end{array}$$

(Benetsy et al., 2008), which is 1.35 mm for the W-band. Here, a spacing of 1 mm was chosen. The total length of the line aperture was L_Ap = 400 mm. The PE test object was positioned in such a way that its front plateau (see Fig. 3) was orientated parallel to the line aperture at a distance of $z_{min}=\mathrm{25.8}$ cm. Thus, the field of view of the reconstructed image needs to reach up to $z_{max}=\mathrm{31.8}$ cm in the range direction (see Fig. 3). Table 1 sums up the parameters of the measurements.

The system is calibrated by two calibration measurements (Gumbmann, 2011):

• Load standard: an empty space measurement with no reflecting object to eliminate crosstalk between the antennas;

• short standard: a measurement with a metal plate placed in front of the aperture at a defined reference distance d_ref to eliminate the frequency response of the components (network analyser, extenders, antennas and cables).

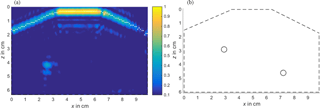
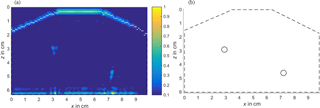
Figure 5 (a) Free-space reconstruction and detected object contour (white); (b) ideal geometry sketch of the object under test.

The raw data s_Rx,raw were then calibrated by

$$\begin{array}{}\text{(22)}& s_{\mathrm{R}x,\mathrm{cal}}=-\mathrm{1}\cdot e^{-j{\mathit{\phi }}_{\mathrm{ref}}}\cdot {\displaystyle \frac{s_{\mathrm{R}x,\mathrm{raw}}-\langle s_{\mathrm{R}x,\mathrm{load}}\rangle }{\langle s_{\mathrm{R}x,\mathrm{short}}\rangle -\langle s_{\mathrm{R}x,\mathrm{load}}\rangle }}.\end{array}$$

Here, s_Rx,load and s_Rx,short are the data obtained from the two calibration measurements named above. The notation 〈⋅〉 symbolizes the mean value over a number of measurements (10 in the presented experiments). The factor −1 is the reflection coefficient of the short. The reference phase φ_ref is the phase calculated from the short measurement. It is

$$\begin{array}{}\text{(23)}& {\mathit{\phi }}_{\mathrm{R}x,\mathrm{ref}}=\mathrm{2}k{d}_{\mathrm{ref}}.\end{array}$$

4.2 Results

As a first step, a free-space reconstruction of the calibrated data was performed. Figure 5 shows the reconstruction of the object assuming free-space propagation throughout the whole domain. As a reference for the reconstructed image, a sketch of the DUT's geometry is depicted also. For the sake of simplicity, the object is depicted in a local coordinate system, starting from z=0 at the DUT's front boundary. In the global coordinate system, the object was located at a range of 25.8 cm from the aperture line, as mentioned above. It can be seen that the target at z ≈ 4.5 cm is not depicted within the object. The lower boundary is not visible either. The image is rather defocused, too.

The reconstruction image is normalized to its maximum intensity value. For clutter reduction, all pixels exhibiting a value below 10 % of the maximum value are set to zero. The object's contour is illustrated by dashed lines.

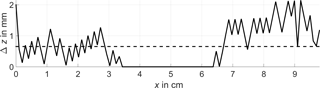
The boundary contour was estimated by a column-wise maximum search as described in Sect. 3.2. The respective points are depicted in white in Fig. 5. For a comparison the estimated boundary is shown in Fig. 6 together with the true contour. It can be seen that the estimation is a good approximation to the real contour: on the upper plateau the estimated values and the analytical ones match perfectly. The error made by the estimation is depicted in Fig. 7. Its mean value is 0.655 mm; the maximum error is 2.14 mm. The estimation displays an uncertainty that is determined by the system's range resolution. For the W-band, whose bandwidth B is 35 GHz, it is

$$\begin{array}{}\text{(24)}& {\mathit{\delta }}_{\mathrm{r}}={\displaystyle \frac{c}{\mathrm{2}B}}=\mathrm{4.3}\mathrm{mm}\end{array}$$

in free space.

Figure 8 shows the image obtained with the described material-sensitive reconstruction algorithm based on the estimated material boundary. Here, Fermat's principle was used for the ray tracing. The concept based on Snell's law was evaluated in the conference paper (Ullmann et al., 2017). Again, the image is normalized to the maximum intensity and all values below 0.1 are neglected. As before, the reference sketch can be seen on the right side of the figure.

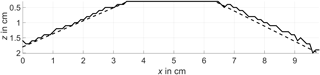
Figure 6 Comparison of the detected material boundary (solid line) and its analytical contour (dashed line).

Figure 7 Estimation error Δz for the material boundary. Dashed line: mean error.

Figure 8 (a) Reconstructed image with estimated boundary (white); (b) ideal geometry sketch.

Note that in the reconstructed images only the targets' upper and lower boundaries are visible. They correspond to the material discontinuities at which reflections occur. From Fig. 8 it can be seen that in contrast to the free-space reconstruction, both targets are reconstructed at their true positions. The improvement in the localization is because in the free-space case the propagation velocity is assumed too high. Consequently, since the velocity is proportional to the traversed way, an overly long distance along the range direction is reconstructed. With the adapted algorithm this error is not made. Furthermore, with the developed method the targets and the material boundary are focused more precisely. Since the lateral resolution depends on the wavelength λ, the aperture length L_Ap and the distance z between the aperture plane and the depicted position

$$\begin{array}{}\text{(25)}& {\mathit{\delta }}_{\mathrm{lat}}={\displaystyle \frac{\mathit{\lambda }\cdot z}{\mathrm{2}\cdot L_{\mathrm{Ap}}}}\end{array}$$

and the range resolution depends on bandwidth and phase velocity (see Eq. 24), a better resolution can be obtained when taking the material characteristics, which affect the phase velocity and the wavelength, into account. From Eqs. (24) and (25) and Table 1 it can be seen that a resolution with theoretical limits of δ_r=2.84 mm in the range direction and δ_lat= 1.04 mm in the lateral direction can be obtained with the described set-up.

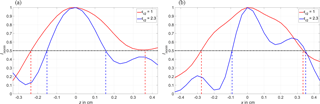
Figure 9 Comparing the resolution of free-space reconstruction (ε_r2 = 1) and material-sensitive reconstruction (ε_r2 = 2.3) on the upper target. (a) Range resolution; (b) lateral resolution.

The actual resolution in the reconstructed images can be estimated from Fig. 9. Here, the point that displayed the maximum intensity at the upper left air inclusion (x ≈ 2.5) was picked out from the datasets depicted in Figs. 5 and 8. The range and lateral resolution can then be estimated by finding the distance Δz or Δx, respectively, between the two points of half the maximum intensity. They are depicted by dashed lines in Fig. 9. For the sake of simplicity and because their z-values do not match, as described previously, the curves are normalized to a dimensionless maximum intensity of 1 and the x-/z-coordinate of the maximum point was set to 0. It can be seen from Fig. 9 that the material-sensitive reconstruction (blue curve) displays a smaller (i.e. higher) resolution in both the range and lateral directions compared to the free-space reconstruction (red curve). Note however that in the material-sensitive reconstruction the upper target is reconstructed by two rather than one point of high intensity (see Fig. 8). This is because the hole with a diameter of 4 mm does not represent a point target for the employed system. Consequently, in Fig. 9 there are two peaks rather than one, and they are overlapping, so that a proper determination of the resolution is difficult.

From Fig. 9 the respective resolutions can be estimated to

• δ_r= 5.99 mm in the free-space reconstruction versus δ_r= 3.08 mm in the material-sensitive reconstruction;

• δ_lat= 6.13 mm in the free-space reconstruction versus δ_lat= 4.26 mm in the material-sensitive reconstruction.

Note that, when instead examining the lower right target (x ≈ 7.5), a lateral resolution of approximately 2.2 mm can be estimated for the material-sensitive reconstruction in the same way as before. Noise as well as the error caused by the boundary estimation are possible reasons for the deviation between the theoretically achievable and practically achieved resolutions.

5 Conclusion

This article presents methods for the detection of subsurface material defects by means of millimetre-wave synthetic aperture radar imaging. The proposed reconstruction algorithm first detects the shape of the object's surface automatically. In the actual reconstruction it takes into account the effects occurring at the surface material discontinuity, namely refraction and the change in phase velocity, thus allowing for a precise reconstruction of the object under test. The required ray tracing through the heterogeneous surrounding can be accomplished using different approaches. Here we presented a way based on Snell's law and one based on Fermat's principle. Both methods are feasible (see Fig. 8 in this paper and Fig. 5 in Ullmann et al., 2017); however, compared to the ray tracing based on Fermat's principle, the method based on Snell's law requires the extra step of determining the difference angle δ between the vertical and the normal in the respective boundary point.

An experimental verification was conducted by reconstructing a polyethylene object with air inclusions. Here, the proposed algorithm displayed a higher resolution compared to a conventional free-space reconstruction since the lateral resolution depends on the wavelength and the range resolution depends on the phase velocity.