Study of different magneto-optic materials for current sensing applications

This article discusses the properties of different diamagnetic and paramagnetic materials for a basic current/magnetic field sensor system set up with different relative orientations of analyzers and polarizers. The paper analyzes linearity ranges of different materials and their sensitivity for different wavelengths. Terbium doped glass (TDG), terbium gallium garnet (TGG), doped TGG and dense flint glass materials are used for analysis based on Faraday's rotation principle. TGG shows high Faraday rotation, temperature stability and high optical quality. Three ranges of the magnetic field have been chosen for performance analysis. The study reveals that doping of praseodymium (Pr³⁺) on TGG exhibits a better response at 532 nm as well as 1064 nm wavelengths than TGG. At 632.8 nm wavelength, cerium (Ce³⁺) doped terbium aluminum garnet (TAG) ceramic exhibits better resolution than others. The study has been done for performance analysis of different MO sensors applicable for measurement of various process parameters like current, displacement, and magnetic field.

1 Introduction

This article is based on analysis of linearity and sensitivity of different magneto-optic (MO) materials. The applications of magnetic materials are gaining importance in wide fields like industry, defense, astronomy and materials. More research is being carried out in developing new material. Magnetic materials are important media for data handling like data processing, saving and retrieving. Smart card and magnetic strip scanning systems are the most commonly and vastly used applications of the MO effect in our day-to-day life. Various magnetic materials are available, such as diamagnetic, paramagnetic, ferromagnetic and ferrimagnetic. Magnetic materials can be made optically sensitive by doping them with rare earth ions. There are 17 types of rare earth elements available on earth, but the most commonly used are yttrium (Y), neodymium (Nd), gadolinium (Gd), terbium (Tb) and dysprosium (Dy). Chen et al. (2016a, b), Villaverde et al. (1978), and Booth and White (1984) have used rare earth garnets for their study.

In 1845, Faraday found that if a glass block is kept under a strong magnetic field, it becomes optically active (as reported in Jenkins and White, 1976). Optically active material changes the plane of polarization of a linearly polarized light when placed in a magnetic field. This property can be utilized in designing various sensors if the change in magnetic field can be associated with any physical variable. It offers non-contact sensing techniques for measurement of any parameter like current, displacement, and magnetic field. It has gained so much popularity because of many advantages over traditional sensing techniques like its immunity to electromagnetic interference, stray capacitance as well as environmental effect. The sensor is highly reliable with a quick response. Transmitting and receiving optical data have minimum loss and are least affected by noise compared to other means of measurement. The Faraday effect can be used for solid, liquid as well as gaseous media. MO materials must have high Verdet constants and high optical transparency for effective performance. The magneto-optical sensor provides a new perspective in sensor designing and testing.

The material used to design the sensor is called Faraday active material or magneto-optic material and the rotation of the polarization plane is called Faraday rotation (Hecht, 1987; Jenkins and White, 1976; Shurcliff, 1962). Faraday rotation (θ) is proportional to change in magnetic flux density B and total optical path length L. V_verdet is the proportionality constant and is called a Verdet constant. Materials which have paramagnetic ions show a high Verdet constant, whereas it usually is very small for most of the materials. One example of material consisting of paramagnetic ions is terbium, which includes terbium doped glass (TDG) and terbium gallium garnet (TGG) as MO materials. The Faraday rotation changes with variation in wavelength of any MO material.

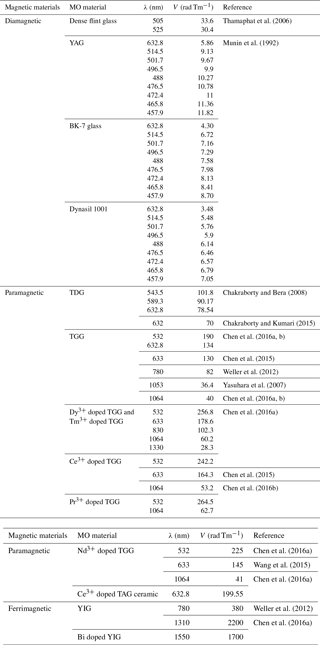
Many scientists have reported various properties of MO materials such as change in Verdet constant with wavelength, temperature dependency and size scalability. Verdet constants of various diamagnetic materials such as fused silica (Dynasil 1001), borosilicate (BK-7) glass and undoped yttrium aluminum garnet (YAG) crystal were calculated by Munin et al. (1992) for different wavelengths in the visible region. It was found that YAG shows a higher Verdet constant than BK-7 and Dynasil at 632.8 nm wavelength. Using the Czochralski (Cz) method, Chen et al. (2016a, b) have fabricated Dy³⁺ doped TGG material and Tm³⁺ doped TGG material. The Verdet constant and magneto-optical characteristics of the materials can be enhanced remarkably by adding rare earth ions. The doped (Ce³⁺, Pr³⁺, Dy³⁺ and Nd³⁺ doping) TGG shows a 20–30 % higher Verdet constant value than pure TGG. Different techniques have been used to measure a Verdet constant of MO materials like pulsed magnetic fields for TGG by Villaverde et al. (1978), the Faraday effect in diamagnetic glass by Thamaphat et al. (2006), and the ellipsometry technique in different media such as flint glass and water by Suchat et al. (2011). Faraday rotation of rare earth garnet material is usually inversely proportional to the wavelength of light, except for yttrium iron garnet (YIG), where the Verdet constant increases above 1300 nm wavelength (Booth and White, 1984). Analysis (Chen et al., 2016a, b) shows that YIG has a poor transparency below 1100 nm. For visible and near-infra-red wavelengths rare earth garnets are implemented for better performance. In 800–1700 nm wavelength, Zhao (2001) found higher rotation and low temperature dependency of YbBi:YIG material. It exhibits higher linearity, sensitivity and accuracy than pure YIG. At 1550 nm wavelength, Huang and Zhang (2002) doped yttrium (Y³⁺) and ytterbium (Yb³⁺) ions in bismuth substituted iron garnet to achieve large rotation and high temperature stability. Koerdt et al. (2003) found the Faraday effect in photonic crystals filled with transparent liquid at 573 nm. Characterization of MO properties of various MO materials is explained by Donati et al. (1988) for a wide range of Vis-NIR wavelengths. In the visible region, Chakraborty and Bera (2008) developed a current sensor based on a null detection technique and Chakraborty and Kumari (2015) designed a magnetic field sensor using a TDG crystal as an MO sensor. A low-cost optical current sensor was designed and demonstrated by Zubia et al. (2013). The characterization of applied tensile stress is studied with in situ magnetic domain imaging and their dynamic behaviors by using magneto-optical Kerr effect (MOKE) microscopy assisted with magneto-optical indicator film (MOIF) (Qiu et al., 2017). Kalska et al. (2008) found a shift in the magneto-optic hysteresis curves due to exchange bias in the temperature-dependent magneto-optic hysteresis curve of “quasi-two-dimensional” arrays. Deeter et al. (1990, 1994), Deeter (1995) and Wolfe et al. (1992) designed a YIG-based magnetic field sensor.

Based on a literature survey it is found that MO sensors are being used in many industrial applications, such as measurement of displacement (Bera and Chakraborty, 2011), magnetic field (Wolfe et al., 1992; Chakraborty and Kumari, 2015), current (Chakraborty and Bera, 2008; Zubia et al., 2013), temperature, and vibration. Several studies are reporting on MO material development and its properties (Munin et al., 1992; Chen et al., 2016a, b; Booth and White, 1984; Chakraborty and Bera, 2008; Chakraborty and Kumari, 2015).

In this context, analysis of sensitivity can be regarded as one of the important performance criteria in sensor design. It shows how the material behaves with the change in particular parameters. Since terbium doped materials exhibit very high rotation, these are very popular and widely used in sensor designing. In this paper we are focusing on various MO materials at different wavelengths and analyzing the sensitivity of a basic magneto-optic setup under different relative orientations of polarizer and analyzer.

2 Theory

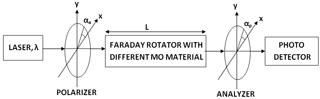
Figure 1 shows the basic block diagram of a magneto-optic measurement setup. For analysis, the basic current measurement setup has been used (Chakraborty and Bera, 2008; Bera and Chakraborty, 2011). It consists of a laser source, polarizer, Faraday rotator, analyzer, and photo-detector to detect the change in plane of polarization. An unpolarized monochromatic light beam coming from the laser source becomes polarized after passing through the polarizer. A linearly polarized monochromatic light beam passes through the magneto-optic material under the influence of a strong magnetic field, and after passing through the analyzer, the beam is received by the photo-detector.

Figure 1 Schematic diagram of the basic magneto-optic measurement system.

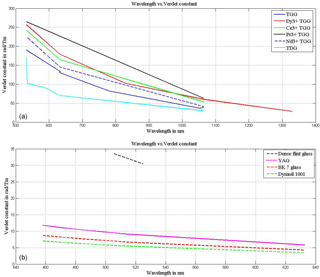
Figure 2 Verdet constant (rad Tm⁻¹) versus wavelength (nm) plot for (a) paramagnetic and (b) diamagnetic materials.

The polarization devices can be expressed in many forms, such as the Mueller matrix, Jones matrix and state of polarization of light by a Poincare sphere. In this article, the Mueller matrix approach has been considered for the calculation. As written in Eq. (1), the output intensity (I_out) of a light beam can be expressed in terms of the Mueller matrix of a Faraday rotator (M_rot), the Mueller matrix of an analyzer (M_ana) and the Stokes vector (S_in) of the linearly polarized input beam (I₀).

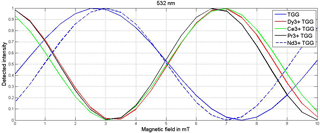
Figure 3 Variation of detected intensity (I_out) with magnetic field (mT) at the 532 nm wavelength of TGG, Dy³⁺ doped TGG, Ce³⁺ doped TGG, Pr³⁺ doped TGG and Nd³⁺ doped TGG for analyzer angles 48, 47, 50, 47 and 42^∘, respectively (Table 3).

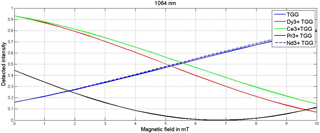
Figure 4 Variation of detected intensity (I_out) with magnetic field (B) wavelength of TGG, Dy³⁺ doped TGG, Ce³⁺ doped TGG, Pr³⁺ doped TGG and Nd³⁺ doped TGG at 1064 nm for analyzer angles 42, 50, 50, 50 and 42^∘, respectively (Table 4).

$$\begin{array}{}\text{(1)}& {\displaystyle }& {\displaystyle }{\mathit{I}}_{\mathrm{out}}=I_{\mathrm{0}}{\mathbf{M}}_{\mathrm{ana}}{\mathbf{M}}_{\mathrm{rot}}{\mathit{S}}_{\mathrm{in}}\text{(2)}& {\displaystyle }& {\displaystyle }{\mathbf{M}}_{\mathrm{ana}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left[\begin{array}{cccc}\mathrm{1}& \cos \mathrm{2}{\mathit{\alpha }}_{\mathrm{a}}& \sin \mathrm{2}{\mathit{\alpha }}_{\mathrm{a}}& \mathrm{0}\\ \cos \mathrm{2}{\mathit{\alpha }}_{\mathrm{a}}& {\cos }^{\mathrm{2}}\mathrm{2}{\mathit{\alpha }}_{\mathrm{a}}& \cos \mathrm{2}{\mathit{\alpha }}_{\mathrm{a}}\sin \mathrm{2}{\mathit{\alpha }}_{\mathrm{a}}& \mathrm{0}\\ \sin \mathrm{2}{\mathit{\alpha }}_{\mathrm{a}}& \cos \mathrm{2}{\mathit{\alpha }}_{\mathrm{a}}& \sin \mathrm{2}{\mathit{\alpha }}_{\mathrm{a}}{\sin }^{\mathrm{2}}\mathrm{2}{\mathit{\alpha }}_{\mathrm{a}}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\end{array}\right]\text{(3)}& {\displaystyle }& {\displaystyle }{\mathbf{M}}_{\mathrm{rot}}=\left[\begin{array}{cccc}\mathrm{1}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \cos \mathrm{2}\mathit{\theta }& -\sin \mathrm{2}\mathit{\theta }& \mathrm{0}\\ \mathrm{0}& \sin \mathrm{2}\mathit{\theta }& \cos \mathrm{2}\mathit{\theta }& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{1}\end{array}\right]\text{(4)}& {\displaystyle }& {\displaystyle }{\mathit{S}}_{\mathrm{in}}=\left[\begin{array}{c}\mathrm{1}\\ \cos \mathrm{2}{\mathit{\alpha }}_{\mathrm{p}}\\ \sin \mathrm{2}{\mathit{\alpha }}_{\mathrm{p}}\\ \mathrm{0}\end{array}\right]\end{array}$$

The transmission angle of the analyzer and polarizer are denoted as α_a and α_p, respectively. The input beam is considered to be a linearly horizontally polarized monochromatic beam. Hence the transmission angle of the polarizer becomes zero. From Eqs. (1) to (4), the expression of the normalized detected intensity of the output beam can be written as in Eq. (5).

$$\begin{array}{}\text{(5)}& {\displaystyle }& {\displaystyle }{I}_{\mathrm{norm}}=\left[{\cos }^{\mathrm{2}}\left(\mathit{\theta }-{\mathit{\alpha }}_{\mathrm{a}}\right)\right]\text{(6)}& {\displaystyle }& {\displaystyle }\mathit{\theta }=V_{\mathrm{verdet}}BL\end{array}$$

Equation (6) gives the relationship of Faraday rotation (θ) with magnetic flux density (B) and total optical path travelled (L) by the light beam (Wenbo, 2000; Koerdt et al., 2003; Thamaphat et al., 2006; Suchat et al., 2011; Aerssens et al., 2011). Faraday rotation is directly proportional to magnetic flux density (B), total optical path length (L) and the Verdet constant (V_verdet) of material which is the function of wavelength. The Verdet constant of a material can also be expressed in terms of optical constants as given in Eq. (7). Here e, m and c are charge on electron, mass of electron and speed of light, respectively. n is referred to as the refractive index of the material and λ denotes the wavelength of light (Chakraborty and Bera, 2008).

$$\begin{array}{}\text{(7)}& {\displaystyle }{V}_{\mathrm{verdet}}=-{\displaystyle \frac{e\mathit{\lambda }}{\mathrm{2}mc}}{\displaystyle \frac{\mathrm{d}n}{\mathrm{d}\mathit{\lambda }}}\end{array}$$

The MO sensor (Martinez et al., 2005) is becoming popular because of many advantages over traditional sensors. Much work has been done on material analysis and properties. Linearity and sensitivity analysis of the material is a very important aspect of sensor designing. This study focuses on the response of detected intensity which is dependent on magnetic field, wavelength and total optical path length. Here fixed optical path length is considered and analysis has been done for different materials with corresponding Verdet constants for different wavelengths. The response is non-linear: as a result it becomes necessary to study the sensitivity for the entire magnetic field range, which is not constant throughout. In order to analyze this, piecewise linearization needs to be considered about a certain operating point. For our linearity analysis, a linear region was calculated for a magnetic field ranging from 0 to 10 mT. Observed response curves shown in Figs. 3–5 are for 0 to 10 mT magnetic flux density where the linear region was evaluated. For this analysis, 5 mT operating points were considered about which the sensitivity has been calculated.

$$\begin{array}{}\text{(8)}& {\displaystyle }\mathrm{Sensitivity}=\left|{\displaystyle \frac{\mathrm{d}{I}_{\mathrm{norm}}}{\mathrm{d}B}}\right|\end{array}$$

Sensitivity is derived from Eq. (8) and can be written as shown in Eq. (9).

$$\begin{array}{}\text{(9)}& \mathrm{Sensitivity}=\left[-\mathrm{2}\sin \mathrm{2}\left(V_{\mathrm{verdet}}BL-{\mathit{\alpha }}_{\mathrm{a}}\right)\times VL\right]\end{array}$$

The smallest measurable change in input which is detected with certainty by the sensor or instrument is known as the resolution of the instrument. Resolution is another performance characteristic which is analyzed and discussed in this paper. Table 1 lists the Verdet constant of different MO materials at different wavelengths. Ferrimagnetic materials show a higher Faraday rotation, but the response is nonlinear.

Table 1 Verdet constants of various MO materials.

Table 2 Work done by various researchers.

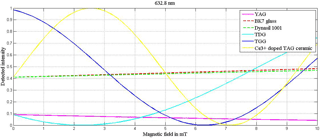
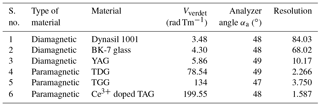
Figure 5 Detected intensity versus magnetic field curve at 632.8 nm wavelength of YAG, BK-7 glass, fused glass, TGG, TDG and Ce³⁺ doped TAG ceramic for analyzer angles 49, 48, 48, 47, 49 and 48^∘, respectively (Table 5).

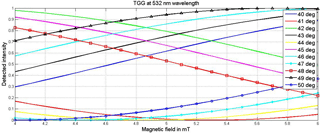
Figure 6 Variation in detected intensity with an analyzer angle from 40 to 50^∘ of TGG at operating point 5 mT.

Table 3 Maximum sensitivity achieved at 532 nm wavelength for magnetic field range 0–10 mT (corresponding to Fig. 3).

In this paper, we have compiled the Verdet constant of different MO materials at various wavelengths. For analysis several observations of the detected intensity have been made with variation in magnetic flux density. Sensitivity and resolution have been found, corresponding to each material. Table 2 shows the performance characteristics done by various researchers for different MO materials.

3 Result

Figure 2a shows the Verdet constant (rad Tm⁻¹) versus wavelength (nm) plot of various paramagnetic MO materials such as TDG, pure TGG and doped TGG (Dy³⁺, Ce³⁺, Pr³⁺ and Nd³⁺ doping). It is observed that the Faraday rotation increases by approximately 20–25 % when TGG is doped with rare earth ions. Pr³⁺ doped TGG gives the highest Faraday rotation of any other rare earth doping. In Fig. 2b the Verdet constant is plotted with change in wavelength for diamagnetic materials. Chen et al. (2016a and b) have found that more than one single paramagnetic ion in garnets can remarkably enhance the Faraday rotation of magneto-optic material. The cubic symmetry of garnet crystals plays an important role in the properties of MO materials. Rare earth (RE) garnets are complex oxides with chemical formula X₃Y₂Z₃O₁₂ (X = RE³⁺, Y and Z = Ga3⁺, Al³⁺ ions).

Ce³⁺ doped TAG has quantum based super-exchange interaction between Tb³⁺ and other paramagnetic RE³⁺ ions which results in an improved Verdet constant.

In this analysis, the range of the magnetic field considered is from 0 to 10 mT and the total optical path length is 30 mm. Equation (5) is used to plot detected intensity with variation in magnetic field as shown in Figs. 3–5.

Table 4 Maximum sensitivity achieved at 1064 nm wavelength for magnetic field range 0–10 mT (corresponding to Fig. 4).

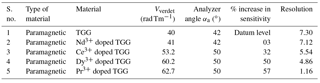
Table 5 Maximum sensitivity achieved at 632.8 nm wavelength for magnetic field range 0–10 mT (corresponding to Fig. 5).

The detected intensity responses with variation in magnetic field density have been plotted using MATLAB 8.0 software. The linearly fit curve equation used was $f\left(x\right)=p_{\mathrm{1}}\times x+p_{\mathrm{2}}$. Here we have considered different relative orientations between analyzer and polarizer angle. In this analysis, a linearly horizontally polarized (α_p=0) monochromatic beam is considered as the input beam and the analyzer angle is varied between 40 and 50^∘ with a change of 1^∘. In the basic Faraday magneto-optic system, when the polarizer angle is in the horizontal direction and the analyzer angle is in the region of 45^∘, a linear response is usually observed. Various plots were achieved and analyzed for diamagnetic and paramagnetic materials at different wavelengths, i.e., 532, 632.8 and 1064 nm.

Figures 3–5 show the response of detected intensity with change in magnetic field density of different MO materials at 532, 1064 and 632.8 nm, respectively. The magnetic flux density range was considered from 0 to 10 mT. Figure 3 shows detected intensity versus magnetic field plot for TGG, Dy³⁺ doped TGG, Ce³⁺ doped TGG, Pr³⁺ doped TGG and Nd³⁺ doped TGG at 532 nm wavelength for analyzer angles 48, 47, 50, 47 and 42^∘. Figure 4 shows the intensity versus magnetic field curve of different materials such as TGG, Dy³⁺ doped TGG, Ce³⁺ doped TGG, Pr³⁺ doped TGG and Nd³⁺ doped TGG at 1064 nm wavelength for analyzer angles 42, 50, 50, 50 and 42^∘. Figure 5 shows the response of detected intensity with the change in magnetic field density for YAG, BK-7 glass, fused glass, TGG, TDG and Ce³⁺ doped TAG ceramic at 632.8 nm wavelength for analyzer angles 49, 48, 48, 47, 49 and 48^∘.

From experimental curves of Figs. 3–5, the sensitivity was expressed in terms of slope for analyzer angle. The results are listed in Tables 3–5 for all the observations achieved for different MO materials.

Figure 6 shows a sample of variation in detected intensity with an analyzer angle from 40 to 50^∘ of TGG at operating point 5 mT. Maximum sensitivity was calculated from this plot for TGG at 532 nm wavelength. The same method was followed to analyze the sensitivity of other materials for different wavelengths.

Table 6 Analyzing linear regions of TGG over a magnetic field range of 0–10 mT at 532 nm wavelength (sample data).

Table 7 Analyzing linear regions of various MO materials over a magnetic field range of 0–10 mT.

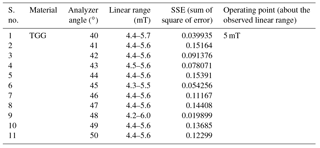
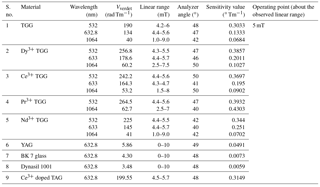
Based on the slope plotted for detected intensity with variation in magnetic flux density, a linear range of MO materials was observed from 4 to 6 mT as mentioned in Table 6 for pure TGG. To find the linear range, a curve fitting toolbox of MATLAB 8.0 has been used. Corresponding to this, sensitivity of the MO materials was analyzed at 5 mT operating point. Further, Table 7 shows the consolidated linear range and sensitivity value of various other MO materials at different wavelengths as available from the literatures mentioned in Table 1.

4 Discussion

Tables 3–5 show different MO materials with their corresponding material types, Verdet constant, analyzer angle α_a (^∘), percentage increase in sensitivity and resolution with respect to pure TGG. The analysis was done for 532, 1064 and 632.8 nm, respectively, and magnetic flux density in the range of 0 to 10 mT.

Doping of pure TGG with different rare earth ions is responsible for the higher Verdet constant. It is observed from Tables 3 and 4 that the sensitivity of the material increases with the Verdet constant. Table 3 shows that at 532 nm wavelength and 47^∘ angle, Pr³⁺ doped TGG material gives maximum sensitivity as compared to any other doped TGG material, which is 30 % higher than pure TGG. At a 50^∘ angle and at 1064 nm wavelength, Pr³⁺ doped TGG material exhibits 57 % higher sensitivity than pure TGG, as shown in Table 4. Amongst diamagnetic and paramagnetic materials, YAG and Ce³⁺ doped TAG ceramic show maximum sensitivity at 49 and 48^∘ angles, respectively, at 632.8 nm wavelength as shown in Table 5.

As detected intensity is the cosine function of θ, shown in Eq. (6), maximum intensity was achieved at 90^∘ and minimum intensity at 0^∘. In order to achieve a linear region, an analyzer angle was considered between 40 and 50^∘. Table 6 shows sample data of TGG for analyzing linear regions over a magnetic field range of 0–10 mT, at 532 nm wavelength. Sum of square error has also been calculated during the analysis. Linear regions of other MO materials shown in Table 7 were calculated by the same method mentioned above, and the operating point is observed as 5 mT (average) over the linear range. The linear region of rare earth ion doped TGG was observed between 4.4 and 5.6 mT, whereas diamagnetic materials show a linear range between 0 and 10 mT, but their sensitivity was low.

In the visible region, YAG material can be used for designing the optical isolator due to its high optical quality (Munin et al., 1992). Dy³⁺ doped TGG is highly transparent MO material and can be used as isolators and for advanced optical communication applications in the visible and near-infrared regions. Also, YIG and Bi doped YIG can be used in the VIS-NIR region as below 1100 nm wavelength they show poor transparency (Chen et al., 2016a, b). Dy³⁺ doped and Tm³⁺ doped TGG show paramagnetic properties below 10 K and between the 10 and 300 K temperature range, respectively (Chen et al., 2016a and b). Tm³⁺ doped TGG also finds applications in the VIS-NIR region. Ferrimagnetic materials such as iron, nickel and gadolinium show a nonlinear response, though they exhibit high Faraday rotation (Chakraborty and Kumari, 2015). Bismuth added iron garnet also proves a larger Faraday rotation than iron garnet in 0.8–1.7 µm. YIG are mainly used in microwave communication as well as designing of optically based devices like rotators (Chen et al., 2016a, b, 2005). It shows high stability for temperature variation.

Terbium is highly transparent but expensive. It shows high resistance to laser damage as well as high thermal conductivity. The TDG sensor has been used for measurement of current, displacement, magnetic field, high-pulse energy lasers, and so on. Size scalability is poor in TDG, whereas it is not a problem for TGG. Yasuhara et al. (2007) have reported that TGG can be used for high-power applications due to excellent thermal conductivity (4.5–7.4 W mK⁻¹). Large-size TGG can be developed by different techniques.

5 Conclusion

TGG and doped TGG are studied extensively for two wavelengths 532 and 1064 nm. Different sensitivities are obtained corresponding to doping of different rare earth ions. Analysis shows that Pr³⁺ doped TGG gives maximum sensitivity over pure TGG as well as any other doped TGG material. At 532 nm wavelength, a 30 % increase in sensitivity can be achieved with doping of a Pr³⁺ rare earth ion on TGG. It is observed that a 57 % increase in sensitivity can be achieved with doping of a Pr³⁺ rare earth ion on TGG at 1064 nm wavelength. This difference in increase can be justified by the higher value of the Verdet constant of the material at the two different wavelengths, which in turn reflects higher rotation. Diamagnetic materials show a linear range but low sensitivity from 0 to 10 mT. TGG crystal is useful in sensor application, due to its size scalability. Paramagnetic materials can be used for the visible and NIR regions. However, ferrimagnetic materials are useful for the IR region because poor transparency is observed below 1100 nm. It is used for measurement of various parameters like current, magnetic field, and displacement. Any variable which can be expressed in terms of magnetic field (current) or displacement can be used for measurement using the MO sensor setup. The magneto-optic materials are extensively used in micro-optic devices such as switches, optical/Faraday isolators, modulators, and deflectors for fiber-optic devices.