Precise linear measurements using a calibrated reference workpiece without temperature measurements

We suggest a procedure for the correction of the errors caused by thermal expansion of a workpiece and the scale of a linear measuring instrument (coordinate measuring machines, length measuring machines, etc.) when linear measurements are performed at nonstandard temperature. We use a calibrated reference workpiece but do not require temperature measurements. An estimation of the measurement uncertainty and application examples are given.

1 Introduction

Quality control loops in today's production in most cases rely on the measurement of geometrical quantities. One problem that might arise is that geometrical properties are specified at 20 ^∘C, the so-called normal temperature (ISO 1:2016-12, 2016). In practice, the temperature in a workshop or a production line will not be adjusted to normal temperature but undergo considerable fluctuations due to various factors which need to be studied and taken into account (Baldo and Donatelli, 2012). Measurement values of geometrical parameters taken at non-normal temperature will be erroneous due to thermal expansion of the material (ISO/TR 16015:2003, 2003).

As a solution, production sites have to be equipped with measuring chambers with specified and controlled equipment. Besides the high maintenance costs of these measurement areas it takes time to bring the manufactured workpieces (WPs) there and to get the required temperature balance between the measuring instrument and the parts to be measured (ISO 15530-3:2011, 2011). Control loops will thus become slow and changing influence factors might therefore cause a certain number of workpieces to be produced out of tolerance before the process can be stabilized again.

Nowadays, the temperature compensation problem is usually solved by a detailed study of the metrological properties of the applied measuring instrument in particular, the whole measuring process in general and hence by a correction of errors due to these properties. This is performed either indirectly – using an “ideal workpiece” that does not change its geometrical properties due to temperature changes to make a comparison of “what we expect” (nominal values) with “what we have” (measured values) (Baldo and Donatelli, 2012; Ohnishi et al., 2010) or directly – when a straight analysis of “what we have” is made (to discover possible factors that might have affected the measured results and therefore to exclude or minimize them) (Chenyang et al., 2011; Kruth et al., 2001). Despite these two approaches being different according to the principles lying behind them, they have something in common. They all require highly qualified personnel to carry out all the tests and measuring temperature of all involved objects (even in the case of using some ideal workpiece, the temperature of the measuring instrument has to be determined).

Some precise complex measuring instruments like coordinate measuring machines (CMMs) are equipped with thermal sensors for detecting temperature from both its linear scales and the object to be measured. That will allow these measuring instruments to estimate the length of the object reduced to a temperature of 20 ^∘C. Manufacturers are expected to have enough funds for all required (the described above) equipment to provide all necessary studies. However, in spite of the potential availability of advanced technologies able to provide automatic temperature compensation, they are not always affordable. This might lead to a bigger uncertainty contribution during production processes and post-production control. As an example, in Ukraine (where the author Dmytro Sumin was born and raised) this is often the case when companies try to provide some small production activity using obsolete (sometimes dozens of years old) but cheap equipment.

In this research work a method is described which would allow companies like these to have an affordable alternative to the expensive equipment, which at the same time is comparably effective. The authors accept the challenge to perform length measurements under non-normal temperature by using calibrated reference workpieces (RWPs, therefore using the indirect approach) but without a seemingly inevitable necessity to measure temperature, neither of the objects to be measured nor of the measuring instrument. In Sect. 2 the procedure for correction of thermal expansion of a workpiece without knowledge of the temperature by referring to a calibrated reference workpiece is introduced. In Sect. 3 the uncertainty of the measurements is estimated and in Sect. 4 application examples are given.

2 Correction of temperature effects during length measurements using a reference workpiece

Thermal expansion is characterized with the coefficient of thermal expansion (CTE) (ISO/TR 16015:2003, 2003):

$$\begin{array}{}\text{(1)}& {\displaystyle }\mathit{\alpha }={\displaystyle \frac{\mathrm{1}}{l_{\mathrm{st}}}}\cdot {\displaystyle \frac{\mathrm{\Delta }l}{\mathrm{\Delta }t}},\end{array}$$

where Δl is the absolute length expansion of a body at the temperature range Δt and l_st is the length at standard temperature.

Using Eq. (1), Δl can be calculated as

$$\begin{array}{}\text{(2)}& {\displaystyle }\mathrm{\Delta }l=l_{\mathrm{st}}\cdot \mathit{\alpha }\cdot \mathrm{\Delta }t.\end{array}$$

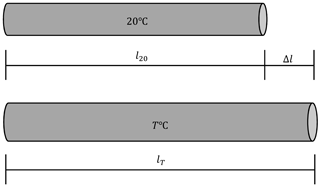
Taking into account Eq. (2) the length l_T (see Fig. 1) of a body at its temperature can be estimated:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }T=\mathrm{20}{}^{\circ }\mathrm{C}+\mathrm{\Delta }t\\ \text{(3)}& {\displaystyle }& {\displaystyle }{l}_T=l_{\mathrm{20}}+\mathrm{\Delta }l=l_{\mathrm{20}}\left(\mathrm{1}+\mathit{\alpha }\cdot \mathrm{\Delta }t\right),\end{array}$$

where l₂₀ is the length of the body at 20 ^∘C.

Figure 1 Expansion of an object due to temperature change.

Equation (2) is a mathematical model of thermal expansion of an object. It is a linear function. So the value of Δl is proportional to the active parameter Δt.

The nominal length of the produced workpiece is defined at the standard temperature 20 ^∘C. If the measurement is executed at a different temperature Δt_wp, the workpiece has the actual length $l_{\mathrm{wp}}^{\mathrm{act}}$ that is related to the length value at $\mathrm{20}{}^{\circ }\mathrm{C},l_{\mathrm{20}\mathrm{wp}}$, described by the following equation:

$$\begin{array}{}\text{(4)}& {\displaystyle }{l}_{\mathrm{20}\mathrm{wp}=}{\displaystyle \frac{l_{\mathrm{wp}}^{\mathrm{act}}}{\mathrm{1}+{\mathit{\alpha }}_{\mathrm{wp}}\mathrm{\Delta }{t}_{\mathrm{wp}}}},\end{array}$$

where α_wp is the CTE of the workpiece and the value ${\left(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{wp}}\mathrm{\Delta }{t}_{\mathrm{wp}}\right)}^{-\mathrm{1}}$ is the characterization of the absolute expansion of the workpiece.

The main problem of this formula is that Δt_wp and $l_{\mathrm{wp}}^{\mathrm{act}}$ must be known first. To estimate them a thermometer and a calliper, for example, can be used. But the calliper is also a material object, with a scale that has some CTE α_sc and at the temperature difference value Δt_sc its length is $l_{\mathrm{sc}}^{\mathrm{act}}$. Also, equality of corresponding parameters should not be expected, so it is assumed that Δt_wp≠Δt_sc and α_wp≠α_sc.

$$\begin{array}{}\text{(5)}& {\displaystyle }{l}_{\mathrm{20}\mathrm{sc}}={\displaystyle \frac{l_{\mathrm{sc}}^{\mathrm{act}}}{\mathrm{1}+{\mathit{\alpha }}_{\mathrm{sc}}\mathrm{\Delta }{t}_{\mathrm{sc}}}},\end{array}$$

where the value ($\mathrm{1}+{\mathit{\alpha }}_{\mathrm{sc}}\mathrm{\Delta }{t}_{\mathrm{sc}}{)}^{-\mathrm{1}}$ characterizes the absolute expansion of the scale.

Figure 2 Behavior of the object at different temperatures.

The actual value of the workpiece's length $l_{\mathrm{wp}}^{\mathrm{act}}$ is unknown and instead of it its measured (estimated) value l_wp will be operated with. Obviously, this value (as well as $l_{\mathrm{wp}}^{\mathrm{act}}$) relates to the absolute expansion of the workpiece. However, because it is measured (estimated) using the scale, it is also related to the absolute expansion of the scale. For better understanding of how this relation works and how it affects the results of measurements, two special cases will be considered.

• a.

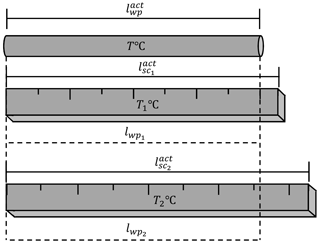
  Changing temperature of the workpiece with constant temperature of the scale:

  In Fig. 2 it can be seen that the workpiece initially had the temperature T₁ ^∘C, thus its actual length was $l_{{\mathrm{wp}}_{\mathrm{1}}}^{\mathrm{act}}$, then its temperature became T₂ ^∘C (and the length $l_{{\mathrm{wp}}_{\mathrm{2}}}^{\mathrm{act}}$), whereas the scale had the same temperature T ^∘C (the length $l_{\mathrm{sc}}^{\mathrm{act}}=\mathrm{const}$) in both cases.

  Estimated values $l_{{\mathrm{wp}}_{\mathrm{1}}}$ and $l_{{\mathrm{wp}}_{\mathrm{2}}}$ (the readings from the scale) showed themselves to be directly proportional to the parameters $l_{{\mathrm{wp}}_{\mathrm{1}}}^{\mathrm{act}}$ and $l_{{\mathrm{wp}}_{\mathrm{2}}}^{\mathrm{act}}$ correspondingly: an increment of $l_{\mathrm{wp}}^{\mathrm{act}}$ leads to an increment of l_wp:

  $$\begin{array}{}\text{(6)}& {\displaystyle \frac{l_{{\mathrm{wp}}_{\mathrm{1}}}}{l_{{\mathrm{wp}}_{\mathrm{1}}}^{\mathrm{act}}}}={\displaystyle \frac{l_{{\mathrm{wp}}_{\mathrm{2}}}}{l_{{\mathrm{wp}}_{\mathrm{2}}}^{\mathrm{act}}}}.\end{array}$$
• b.

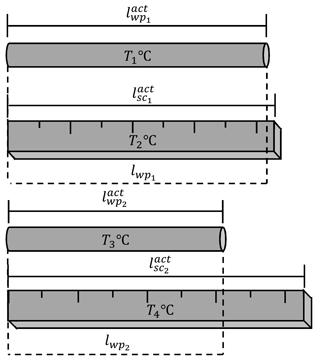
  Changing temperature of the scale with constant temperature of the workpiece:

  In Fig. 3 it is seen that the workpiece had the constant temperature T ^∘C (and the length $l_{\mathrm{wp}}^{\mathrm{act}}=\mathrm{const}$), whereas the scale initially had the temperature T₁ ^∘C (the length $l_{{\mathrm{sc}}_{\mathrm{1}}}^{\mathrm{act}}$), then its temperature became T₂ ^∘C (the length $l_{{\mathrm{sc}}_{\mathrm{2}}}^{\mathrm{act}}$).

  Estimated values $l_{{\mathrm{wp}}_{\mathrm{1}}}$ and $l_{{\mathrm{wp}}_{\mathrm{2}}}$ showed themselves to be inversely proportional to the parameters $l_{{\mathrm{sc}}_{\mathrm{1}}}^{\mathrm{act}}$ and $l_{{\mathrm{sc}}_{\mathrm{2}}}^{\mathrm{act}}$ correspondingly: an increment of $l_{\mathrm{sc}}^{\mathrm{act}}$ leads to a decrement of l_wp:

  $$\begin{array}{}\text{(7)}& {\displaystyle }{l}_{{\mathrm{wp}}_{\mathrm{1}}}\cdot l_{{\mathrm{sc}}_{\mathrm{1}}}^{\mathrm{act}}=l_{{\mathrm{wp}}_{\mathrm{2}}}\cdot l_{{\mathrm{sc}}_{\mathrm{2}}}^{\mathrm{act}}.\end{array}$$

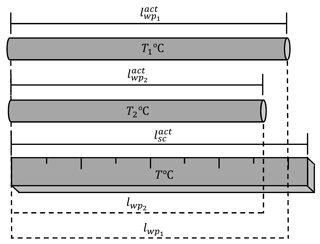
In real life changing of both parameters $l_{\mathrm{sc}}^{\mathrm{act}}$ and $l_{\mathrm{wp}}^{\mathrm{act}}$ at the same time (see Fig. 4) is mostly the case.

Figure 3 Behavior of the scale at different temperatures.

Figure 4 Behavior of both objects at different temperatures.

The workpiece had the temperature T₁ ^∘C (the length $l_{{\mathrm{wp}}_{\mathrm{1}}}^{\mathrm{act}}$) and the scale had the temperature T₂ ^∘C (the length $l_{{\mathrm{sc}}_{\mathrm{1}}}^{\mathrm{act}}$), then they both changed their temperatures to the values T₃ ^∘C (the length $l_{{\mathrm{wp}}_{\mathrm{2}}}^{\mathrm{act}}$) and T₄ ^∘C (the length $l_{{\mathrm{sc}}_{\mathrm{2}}}^{\mathrm{act}}$) correspondingly. The way that the parameter l_wp relates to the parameters $l_{\mathrm{wp}}^{\mathrm{act}}$ and $l_{\mathrm{sc}}^{\mathrm{act}}$ is already known from Eqs. (6) and (7), so taking these into account, a new proportion can be derived:

$$\begin{array}{}\text{(8)}& {\displaystyle }{l}_{{\mathrm{wp}}_{\mathrm{1}}}\cdot {\displaystyle \frac{l_{{\mathrm{sc}}_{\mathrm{1}}}^{\mathrm{act}}}{l_{{\mathrm{wp}}_{\mathrm{1}}}^{\mathrm{act}}}}=l_{{\mathrm{wp}}_{\mathrm{2}}}\cdot {\displaystyle \frac{l_{{\mathrm{sc}}_{\mathrm{2}}}^{\mathrm{act}}}{l_{{\mathrm{wp}}_{\mathrm{2}}}^{\mathrm{act}}}}.\end{array}$$

If we assume all parameters with subscript “1” (the left side of Eq. 8) to have been achieved at Δt_wp=0 K and Δt_sc=0 K, according to Eqs. (4) and (5), it can be stated that

$$\begin{array}{}\text{(9)}& {\displaystyle }{l}_{\mathrm{20}\mathrm{wp}}\cdot {\displaystyle \frac{l_{\mathrm{20}\mathrm{sc}}}{l_{\mathrm{20}\mathrm{wp}}}}=l_{\mathrm{wp}}\cdot {\displaystyle \frac{l_{\mathrm{sc}}^{\mathrm{act}}}{l_{\mathrm{wp}}^{\mathrm{act}}}}.\end{array}$$

For further calculations it will be assumed that l_20 sc=l_20 wp (the scale is expected not to be deformed by temperature effects at Δt_sc=0 K). After transformation of Eq. (9), l_20 wp can be found as follows:

$${\displaystyle }{l}_{\mathrm{20}\mathrm{wp}}=l_{\mathrm{wp}}\cdot {\displaystyle \frac{l_{\mathrm{sc}}^{\mathrm{act}}}{l_{\mathrm{wp}}^{\mathrm{act}}}}=l_{\mathrm{wp}}\cdot {\displaystyle \frac{\mathrm{1}+{\mathit{\alpha }}_{\mathrm{sc}}\mathrm{\Delta }{t}_{\mathrm{sc}}}{\mathrm{1}+{\mathit{\alpha }}_{\mathrm{wp}}\mathrm{\Delta }{t}_{\mathrm{wp}}}}$$

or

$$\begin{array}{}\text{(10)}& {\displaystyle }{l}_{\mathrm{20}\mathrm{wp}}=l_{\mathrm{wp}}\cdot {\displaystyle \frac{\mathrm{1}+{\mathit{\alpha }}_{\mathrm{sc}}\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}}{\mathrm{1}+{\mathit{\alpha }}_{\mathrm{wp}}\mathrm{\Delta }{t}_{\mathrm{wp}}}},\end{array}$$

where $\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}$ is the temperature of the scale during measurements of l_wp.

It is clearly seen that in the case of equality of absolute expansion characterization values of the workpiece and the scale ($\mathrm{1}+{\mathit{\alpha }}_{\mathrm{sc}}\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}=\mathrm{1}+{\mathit{\alpha }}_{\mathrm{wp}}\mathrm{\Delta }{t}_{\mathrm{wp}}$) even if $\mathrm{\Delta }{t}_{\mathrm{wp}}\ne \mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}$ and α_wp≠α_sc, the temperature effect is cancelled and the desired value l_20 wp therefore can be achieved without any additional action. However, such an instance is a rare case. To use Eq. (10) we should figure out each of these four unknown parameters: α_wp, α_sc, Δt_wp and $\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}$. Even if a thermometer was used so that Δt_wp and $\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}$ could be found, the CTEs nevertheless may not be calculated directly, but only achieved after a series of measurements (Amatuni, 1972).

Analyzing Eq. (10), it can be discovered that l_wp and l_20 wp are related to each other through a term which contains all four unknown parameters. This means that if a checked workpiece were used as the reference standard (ISO/TR 16015:2003, 2003; ISO 15530-3:2011, 2011) (a so-called reference workpiece), Eq. (10) would be as follows:

$$\begin{array}{}\text{(11)}& {\displaystyle }{l}_{\mathrm{20}\mathrm{rwp}}=l_{\mathrm{rwp}}\cdot {\displaystyle \frac{\mathrm{1}+{\mathit{\alpha }}_{\mathrm{sc}}\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}}{\mathrm{1}+{\mathit{\alpha }}_{\mathrm{rwp}}\mathrm{\Delta }{t}_{\mathrm{rwp}}}},\end{array}$$

where l_rwp and l_20 rwp are the length of the reference workpiece at Δt_rwp≠0 K and Δt_rwp=0 K correspondingly, $\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}$ is the temperature difference at the scale during measurements of l_rwp, α_rwp is the CTE of the reference workpiece and α_sc remains unchanged as we are using the same measuring instrument.

Now it is necessary to check these workpieces using the same measuring instrument as a comparator (ISO/TR 16015:2003, 2003). If the reference workpiece's CTE and its temperature were α_rwp=α_wp and Δt_rwp=Δt_wp correspondingly and the temperature of the scale during the reference workpiece measurements were $\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}=\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}$ (assuming that all objects' temperature distribution is uniform), it would be able to decrease the number of four unknown parameters to only one, combining Eqs. (10) and (11) to a proportion

$$\begin{array}{}\text{(12)}& {\displaystyle \frac{l_{\mathrm{20}\mathrm{wp}}}{l_{\mathrm{wp}}}}={\displaystyle \frac{l_{\mathrm{20}\mathrm{rwp}}}{l_{\mathrm{rwp}}}}.\end{array}$$

Only l_20 rwp is now needed. As long as the value l_20 rwp is measured at 20 ^∘C in a laboratory and provided to us, Eq. (12) will not have any unknown parameters (out of the four stated above) anymore.

The desired value l_20 wp in this case could be found as

$$\begin{array}{}\text{(13)}& {\displaystyle }{l}_{\mathrm{20}\mathrm{wp}}={\displaystyle \frac{l_{\mathrm{20}\mathrm{rwp}}\cdot l_{\mathrm{wp}}}{l_{\mathrm{rwp}}}}.\end{array}$$

Using the reference workpiece according to Eq. (13), we can find out l_20 wp for any other workpiece of the same type (with the same desired geometrical parameter) without knowing α_wp, α_sc, t_wp and $t_{\mathrm{sc}}^{\mathrm{wp}}$. The components l_wp and l_rwp in Eq. (13) are estimated (not actual!) values achieved using the scale of a measuring instrument. Because usually the scale's CTE has a nonzero value and expands too, the differences l_rwp−l_20 rwp and l_wp−l_20 wp show the so-called relative expansion of the workpiece compared to the scale which will be smaller than the expected absolute expansion of the workpiece (e.g., $l_{\mathrm{wp}}^{\mathrm{act}}-l_{\mathrm{20}\mathrm{wp}}$ in Eq. 4).

3 Estimation of uncertainty

It is assumed that three of the four corresponding parameters are equal: α_rwp=α_wp, Δt_rwp=Δt_wp and $\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}=\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}$ (α_sc=const). But, it is clear, that in real life they never are; even CTEs of two different objects made from one material may be slightly different. Also, despite the fact that it is required that the reference workpiece and the workpiece to be measured are similar (within certain tolerances) (ISO 15530-3:2011, 2011), there might be some difference between geometrical and physical properties of the workpiece and the reference workpiece.

Using Eqs. (10), (11) and (13) without making simplifying assumptions, it can be stated that

$$\begin{array}{}\text{(14)}& {\displaystyle }{l}_{\mathrm{20}\mathrm{wp}}={\displaystyle \frac{l_{\mathrm{20}\mathrm{rwp}}{l}_{\mathrm{wp}}\left(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{sc}}\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\right)\left(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{rwp}}\mathrm{\Delta }{t}_{\mathrm{rwp}}\right)}{l_{\mathrm{rwp}}\left(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{wp}}\mathrm{\Delta }{t}_{\mathrm{wp}}\right)\left(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{sc}}\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)}},\end{array}$$

where $\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}$ and $\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}$ are the temperature differences at the scale during measurements of l_wp and l_rwp.

Uncertainty of the measurements can be estimated using Eq. (14) as a mathematical model of measurements (JCGM 100:2008, 2008). After a series of transformations it will look like

$$\begin{array}{ll}\text{(15)}& {\displaystyle }& {\displaystyle }{l}_{\mathrm{20}\mathrm{wp}}={\displaystyle }& {\displaystyle \frac{l_{\mathrm{20}\mathrm{rwp}}{l}_{\mathrm{wp}}\left(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{rwp}}\mathrm{\Delta }{t}_{\mathrm{rwp}}+{\mathit{\alpha }}_{\mathrm{sc}}\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}+{\mathit{\alpha }}_{\mathrm{rwp}}{\mathit{\alpha }}_{\mathrm{sc}}\mathrm{\Delta }{t}_{\mathrm{rwp}}\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\right)}{l_{\mathrm{rwp}}\left(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{wp}}\mathrm{\Delta }{t}_{\mathrm{wp}}+{\mathit{\alpha }}_{\mathrm{sc}}\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}+{\mathit{\alpha }}_{\mathrm{wp}}{\mathit{\alpha }}_{\mathrm{sc}}\mathrm{\Delta }{t}_{\mathrm{wp}}\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)}}.\end{array}$$

In Eq. (15) ${\mathit{\alpha }}_{\mathrm{rwp}}{\mathit{\alpha }}_{\mathrm{sc}}\mathrm{\Delta }{t}_{\mathrm{rwp}}\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\to \mathrm{0}$ and ${\mathit{\alpha }}_{\mathrm{wp}}{\mathit{\alpha }}_{\mathrm{sc}}\mathrm{\Delta }{t}_{\mathrm{wp}}\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\to \mathrm{0}$ at any natural conditions, so the formula can be shown as

$$\begin{array}{}\text{(16)}& {\displaystyle }{l}_{\mathrm{20}\mathrm{wp}}={\displaystyle \frac{l_{\mathrm{20}\mathrm{rwp}}{l}_{\mathrm{wp}}}{l_{\mathrm{rwp}}}}\cdot {\displaystyle \frac{\left(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{rwp}}\mathrm{\Delta }{t}_{\mathrm{rwp}}+{\mathit{\alpha }}_{\mathrm{sc}}\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\right)}{\left(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{wp}}\mathrm{\Delta }{t}_{\mathrm{wp}}+{\mathit{\alpha }}_{\mathrm{sc}}\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)}}+\mathrm{\dots }.\end{array}$$

Defining $\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}=\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}$, $\mathrm{\Delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}=\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}$, $\mathrm{\Delta }{t}_{\mathrm{wp}}=\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{wp}}$ and ${\mathit{\alpha }}_{\mathrm{wp}}={\mathit{\alpha }}_{\mathrm{rwp}}+\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}$, Eq. (16) can be shown as

$$\begin{array}{ll}\text{(17)}& {\displaystyle }& {\displaystyle }{l}_{\mathrm{20}\mathrm{wp}}={\displaystyle }& {\displaystyle }f\left(l_{\mathrm{20}\mathrm{rwp}},l_{\mathrm{wp}},l_{\mathrm{rwp}},\mathrm{\Delta }{t}_{\mathrm{rwp}},{\mathit{\alpha }}_{\mathrm{rwp}},{\mathit{\alpha }}_{\mathrm{sc}},\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}},\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}},\mathit{\delta }{t}_{\mathrm{wp}},\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)\\ {\displaystyle }& {\displaystyle }={\displaystyle \frac{l_{\mathrm{20}\mathrm{rwp}}{l}_{\mathrm{wp}}}{l_{\mathrm{rwp}}}}\\ {\displaystyle }& {\displaystyle }\cdot {\displaystyle \frac{\left(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{rwp}}\mathrm{\Delta }{t}_{\mathrm{rwp}}+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\right)\right)}{\left(\mathrm{1}+\left({\mathit{\alpha }}_{\mathrm{rwp}}+\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{wp}}\right)+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)\right)}}.\end{array}$$

The differences $\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}$, $\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}$, δt_wp and δα_wp (but not their uncertainties) are estimated to be zero. The values l_20 rwp, l_wp, l_rwp, Δt_rwp, α_rwp and α_sc are assumed to be uncorrelated. Taking this into account, the combined standard uncertainty can be expressed as

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{u}_{\mathrm{c}}^{\mathrm{2}}\left(l_{\mathrm{20}\mathrm{wp}}\right)=c^{\mathrm{2}}\left(l_{\mathrm{20}\mathrm{rwp}}\right)u^{\mathrm{2}}\left(l_{\mathrm{20}\mathrm{rwp}}\right)+c^{\mathrm{2}}\left(l_{\mathrm{wp}}\right)u^{\mathrm{2}}\left(l_{\mathrm{wp}}\right)\\ {\displaystyle }& {\displaystyle }+c^{\mathrm{2}}\left(l_{\mathrm{rwp}}\right)u^{\mathrm{2}}\left(l_{\mathrm{rwp}}\right)+c^{\mathrm{2}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}\right)u^{\mathrm{2}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}\right)\\ {\displaystyle }& {\displaystyle }+c^{\mathrm{2}}\left({\mathit{\alpha }}_{\mathrm{rwp}}\right)u^{\mathrm{2}}\left({\mathit{\alpha }}_{\mathrm{rwp}}\right)+c^{\mathrm{2}}\left({\mathit{\alpha }}_{\mathrm{sc}}\right)u^{\mathrm{2}}\left({\mathit{\alpha }}_{\mathrm{sc}}\right)+c^{\mathrm{2}}\left(\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\right)u^{\mathrm{2}}\left(\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\right)\\ {\displaystyle }& {\displaystyle }+c^{\mathrm{2}}\left(\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)u^{\mathrm{2}}\left(\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)+c^{\mathrm{2}}\left(\mathit{\delta }{t}_{\mathrm{wp}}\right)u^{\mathrm{2}}\left(\mathit{\delta }{t}_{\mathrm{wp}}\right)\\ \text{(18)}& {\displaystyle }& {\displaystyle }+c^{\mathrm{2}}\left(\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)u^{\mathrm{2}}\left(\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right),\end{array}$$

where the sensitivity factors $c\left(x_i\right)=\frac{\partial \left(f\left(x_{\mathrm{1}},x_{\mathrm{2}},\mathrm{\dots },x_n\right)\right)}{\partial \left(x_i\right)},i=\mathrm{1},\mathrm{2},\mathrm{\dots },n$ are

$$\begin{array}{ll}\text{(19)}& {\displaystyle }& {\displaystyle }c\left(l_{\mathrm{20}\mathrm{rwp}}\right)={\displaystyle }& {\displaystyle \frac{l_{\mathrm{wp}}\left(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{rwp}}\mathrm{\Delta }{t}_{\mathrm{rwp}}+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\right)\right)}{l_{\mathrm{rwp}}\left(\mathrm{1}+\left({\mathit{\alpha }}_{\mathrm{rwp}}+\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{wp}}\right)+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)\right)}},\end{array}$$

$$\begin{array}{ll}\text{(20)}& {\displaystyle }& {\displaystyle }c\left(l_{\mathrm{wp}}\right)={\displaystyle }& {\displaystyle \frac{l_{\mathrm{20}\mathrm{rwp}}\left(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{rwp}}\mathrm{\Delta }{t}_{\mathrm{rwp}}+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\right)\right)}{l_{\mathrm{rwp}}\left(\mathrm{1}+\left({\mathit{\alpha }}_{\mathrm{rwp}}+\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{wp}}\right)+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)\right)}},\end{array}$$

$$\begin{array}{ll}\text{(21)}& {\displaystyle }& {\displaystyle }c\left(l_{\mathrm{rwp}}\right)={\displaystyle }& {\displaystyle }-{\displaystyle \frac{l_{\mathrm{20}\mathrm{rwp}}{l}_{\mathrm{wp}}\left(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{rwp}}\mathrm{\Delta }{t}_{\mathrm{rwp}}+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\right)\right)}{l_{\mathrm{rwp}}^{\mathrm{2}}\left(\mathrm{1}+\left({\mathit{\alpha }}_{\mathrm{rwp}}+\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{wp}}\right)+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)\right)}},\end{array}$$

$$\begin{array}{ll}\text{(22)}& {\displaystyle }& {\displaystyle }c\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}\right)={\displaystyle \frac{l_{\mathrm{20}\mathrm{rwp}}{l}_{\mathrm{wp}}}{l_{\mathrm{rwp}}}}{\displaystyle }& {\displaystyle }\cdot \left({\displaystyle \frac{{\mathit{\alpha }}_{\mathrm{rwp}}+{\mathit{\alpha }}_{\mathrm{sc}}}{\mathrm{1}+\left({\mathit{\alpha }}_{\mathrm{rwp}}+\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{wp}}\right)+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)}}\right.\\ {\displaystyle }& {\displaystyle }\left.-{\displaystyle \frac{\left(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{rwp}}\mathrm{\Delta }{t}_{\mathrm{rwp}}+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\right)\right)\left({\mathit{\alpha }}_{\mathrm{rwp}}+\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}+{\mathit{\alpha }}_{\mathrm{sc}}\right)}{{\left(\mathrm{1}+\left({\mathit{\alpha }}_{\mathrm{rwp}}+\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{wp}}\right)+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)\right)}^{\mathrm{2}}}}\right),\end{array}$$

$$\begin{array}{ll}\text{(23)}& {\displaystyle }& {\displaystyle }c\left({\mathit{\alpha }}_{\mathrm{rwp}}\right)={\displaystyle \frac{l_{\mathrm{20}\mathrm{rwp}}{l}_{\mathrm{wp}}}{l_{\mathrm{rwp}}}}{\displaystyle }& {\displaystyle }\cdot \left({\displaystyle \frac{\mathrm{\Delta }{t}_{\mathrm{rwp}}}{\mathrm{1}+\left({\mathit{\alpha }}_{\mathrm{rwp}}+\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{wp}}\right)+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)}}\right.\\ {\displaystyle }& {\displaystyle }\left.-{\displaystyle \frac{\left(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{rwp}}\mathrm{\Delta }{t}_{\mathrm{rwp}}+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\right)\right)\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{wp}}\right)}{{\left(\mathrm{1}+\left({\mathit{\alpha }}_{\mathrm{rwp}}+\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{wp}}\right)+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)\right)}^{\mathrm{2}}}}\right),\end{array}$$

$$\begin{array}{ll}\text{(24)}& {\displaystyle }& {\displaystyle }c\left({\mathit{\alpha }}_{\mathrm{sc}}\right)={\displaystyle \frac{l_{\mathrm{20}\mathrm{rwp}}{l}_{\mathrm{wp}}}{l_{\mathrm{rwp}}}}{\displaystyle }& {\displaystyle }\cdot \left({\displaystyle \frac{\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}}{\mathrm{1}+\left({\mathit{\alpha }}_{\mathrm{rwp}}+\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{wp}}\right)+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)}}\right.\\ {\displaystyle }& {\displaystyle }\left.-{\displaystyle \frac{\left(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{rwp}}\mathrm{\Delta }{t}_{\mathrm{rwp}}+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\right)\right)\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)}{{\left(\mathrm{1}+\left({\mathit{\alpha }}_{\mathrm{rwp}}+\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{wp}}\right)+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)\right)}^{\mathrm{2}}}}\right),\end{array}$$

$$\begin{array}{ll}\text{(25)}& {\displaystyle }& {\displaystyle }c\left(\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\right)={\displaystyle }& {\displaystyle \frac{l_{\mathrm{20}\mathrm{rwp}}{l}_{\mathrm{wp}}{\mathit{\alpha }}_{\mathrm{sc}}}{l_{\mathrm{rwp}}\left(\mathrm{1}+\left({\mathit{\alpha }}_{\mathrm{rwp}}+\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{wp}}\right)+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)\right)}},\end{array}$$

$$\begin{array}{ll}\text{(26)}& {\displaystyle }& {\displaystyle }c\left(\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)={\displaystyle }& {\displaystyle }-{\displaystyle \frac{l_{\mathrm{20}\mathrm{rwp}}{l}_{\mathrm{wp}}{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{rwp}}\mathrm{\Delta }{t}_{\mathrm{rwp}}+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\right)\right)}{l_{\mathrm{rwp}}{\left(\mathrm{1}+\left({\mathit{\alpha }}_{\mathrm{rwp}}+\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{wp}}\right)+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)\right)}^{\mathrm{2}}}},\end{array}$$

$$\begin{array}{ll}\text{(27)}& {\displaystyle }& {\displaystyle }c\left(\mathit{\delta }{t}_{\mathrm{wp}}\right)={\displaystyle }& {\displaystyle }-{\displaystyle \frac{l_{\mathrm{20}\mathrm{rwp}}{l}_{\mathrm{wp}}\left(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{rwp}}\mathrm{\Delta }{t}_{\mathrm{rwp}}+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\right)\right)\left({\mathit{\alpha }}_{\mathrm{rwp}}+\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)}{l_{\mathrm{rwp}}{\left(\mathrm{1}+\left({\mathit{\alpha }}_{\mathrm{rwp}}+\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{wp}}\right)+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)\right)}^{\mathrm{2}}}}\end{array}$$

and

$$\begin{array}{ll}\text{(28)}& {\displaystyle }& {\displaystyle }c\left(\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)={\displaystyle }& {\displaystyle }-{\displaystyle \frac{l_{\mathrm{20}\mathrm{rwp}}{l}_{\mathrm{wp}}\left(\mathrm{1}+{\mathit{\alpha }}_{\mathrm{rwp}}\mathrm{\Delta }{t}_{\mathrm{rwp}}+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\right)\right)\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{wp}}\right)}{l_{\mathrm{rwp}}{\left(\mathrm{1}+\left({\mathit{\alpha }}_{\mathrm{rwp}}+\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{wp}}\right)+{\mathit{\alpha }}_{\mathrm{sc}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}+\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)\right)}^{\mathrm{2}}}}.\end{array}$$

Uncertainty of the calibration of the reference workpiece u(l_20 rwp) should be taken from the calibration certificate, which states the value and uncertainty of l_20 rwp for the reference workpiece.

The uncertainties of the measured lengths u(l_wp), u(l_rwp) and temperature difference u(Δt_rwp) could be calculated as a standard uncertainty of type A and/or type B after the values l_wp, l_rwp and Δt_rwp were measured by corresponding measurement instruments.

Uncertainty of the reference workpiece's thermal expansion coefficient u(α_rwp) should be taken from the calibration certificate, which states the value and uncertainty of α_rwp for the reference workpiece. The uncertainty for the values l_20 rwp and α_rwp (as well as the values themselves) is provided in the same certificate (a CTE investigation should be specifically carried out for the given object prior to the method application).

Regardless of what the value of c(α_sc) in Eq. (24) is, it was decided to use the same measuring instrument for defining lengths of the reference workpiece and the workpiece, so α_sc itself can not (or, at least, should not) affect values l_rwp and l_wp, and so it will be assumed that c(α_sc)=0 (it is estimated that the CTE of the scale α_sc remains the same during our measurement session). Thus, the standard uncertainty u(δα_sc) (whatever its value is) can be neglected.

The uncertainties of the differences of temperature $u\left(\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\right)$, $u\left(\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)$, u(δt_wp) and the difference of CTEs u(δα_wp) should be considered specifically for the circumstances according to which the values $\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}$, $\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}$, δt_wp and δα_wp were assumed.

Expanded uncertainty U_p with a level of confidence p and coverage factor k_p can be calculated using Eq. (18) as follows:

$$\begin{array}{}\text{(29)}& {\displaystyle }{U}_p=k_p\cdot u_{\mathrm{c}}\left(l_{\mathrm{20}\mathrm{wp}}\right).\end{array}$$

The final estimation $l_{\mathrm{20}\mathrm{wp}}^{\mathrm{act}}$ of the value of l_20 wp therefore can be expressed as

$$\begin{array}{}\text{(30)}& {\displaystyle }{l}_{\mathrm{20}\mathrm{wp}}=l_{\mathrm{20}\mathrm{wp}}\pm U_p.\end{array}$$

The uncertainty of measuring humidity and atmospheric pressure was neglected, as α=f(t) (Amatuni, 1972).

All given formulae are well known and used here as an adaptation for a specific task solution.

4 Practical application

4.1 Example 1

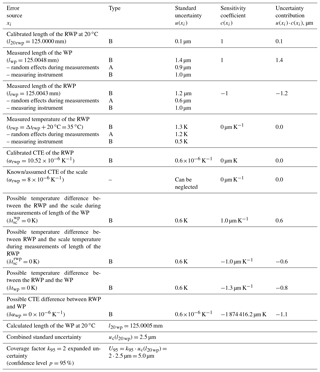
There are two gauge blocks calibrated beforehand which will be used as the WP to be measured using a CMM and the RWP (shown in Fig. 5). The task is to determine the length of a WP (as if it were unknown) at the normal temperature l_20 wp, evaluate the uncertainty of measurements and compare calculated results with actual ones.

Figure 5 The workpiece (upper) and the reference workpiece (lower) on the CMM's table in example 1.

The RWP's properties are known; its length at normal temperature and the CTE are l_20 rwp= 125.0000 mm ± 0.0002 mm and ${\mathit{\alpha }}_{\mathrm{rwp}}=\mathrm{10.52}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}\pm \mathrm{1}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}$, respectively.

Measurements which have been carried out assuming that α_rwp=α_wp give the following values of length of RWP and WP at a current temperature l_rwp=125.0043 mm and l_wp=125.0048 mm.

Using Eq. (13) the desired value can be calculated:

$${\displaystyle }{l}_{\mathrm{20}\mathrm{wp}}={\displaystyle \frac{\mathrm{125.0000}\mathrm{mm}\cdot \mathrm{125.0048}\mathrm{mm}}{\mathrm{125.0043}\mathrm{mm}}}=\mathrm{125.0005}\mathrm{mm}.$$

In this way, the first step of the task is done – l_20 wp is known. Now, all possible uncertainty factors must be considered.

Evaluation of the uncertainty will be done in three steps:

1. calculation of sensitivity factors c(x_i),

2. consideration of standard uncertainty values u(x_i),

3. calculation of combined standard uncertainty u_c(f(x)) and expanded uncertainty U_p.

Before starting this procedure, we will summarize all known arguments and assume all unknown arguments of the function

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{l}_{\mathrm{20}\mathrm{wp}}=\\ {\displaystyle }& {\displaystyle }f\left(l_{\mathrm{20}\mathrm{rwp}},l_{\mathrm{wp}},l_{\mathrm{rwp}},\mathrm{\Delta }{t}_{\mathrm{rwp}},{\mathit{\alpha }}_{\mathrm{rwp}},{\mathit{\alpha }}_{\mathrm{sc}},\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}},\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}},\mathit{\delta }{t}_{\mathrm{wp}},\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right),\end{array}$$

where l_20 wp=125.0005 mm, l_20 rwp=125.0000 mm, l_wp=125.0048 mm, l_rwp= 125.0043 mm, Δt_rwp=15 K, ${\mathit{\alpha }}_{\mathrm{rwp}}=\mathrm{10.52}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}$, ${\mathit{\alpha }}_{\mathrm{sc}}=\mathrm{8}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}=\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}=\mathit{\delta }{t}_{\mathrm{wp}}=\mathrm{0}\mathrm{K}$ and $\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}=\mathrm{0}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}$.

If the parameter α_sc is unknown it can be estimated as any reasonable value; in this very instance it is provided though.

The calibration certificate gives the expanded uncertainty of the l_20 rwp U₉₅=0.0002 mm with coverage factor k=2. The standard uncertainty is then

$${\displaystyle }u\left(l_{\mathrm{20}\mathrm{rwp}}\right)={\displaystyle \frac{U_{\mathrm{95}}}{k}}=\mathrm{0.0001}\mathrm{mm}=\mathrm{0.1}\mathrm{\mu }\mathrm{m}.$$

The value l_wp is achieved as a mean value of five measurements. The standard uncertainty of the measured value can be calculated as a type A standard uncertainty:

$${\displaystyle }u\left(\stackrel{\mathrm{‾}}{l_{\mathrm{wp}}}\right)=\sqrt{{\displaystyle \frac{\sum _i^n{\left(l_{{\mathrm{wp}}_i}-l_{\mathrm{wp}}\right)}^{\mathrm{2}}}{n-\mathrm{1}}}}=\mathrm{0.9}\mathrm{\mu }\mathrm{m}.$$

According to the calibration certificate of the measuring instrument, the expanded uncertainty of measurements with it is given as a distribution range $\pm \left(\mathrm{1.5}+L/\mathrm{500}\right)$ µm, where L (in mm) is the nominal size of the object to be measured, and because the actual value $l_{\mathrm{wp}}^{\mathrm{act}}$ can be anywhere within this range at equal probability, a rectangular law of a random value distribution is to be considered. The standard uncertainty due to a random error of the measuring instrument (mi) is then

$${\displaystyle }u\left(l_{\mathrm{wp}}^{\mathrm{mi}}\right)={\displaystyle \frac{\left(\mathrm{1.5}+\frac{\mathrm{125}}{\mathrm{500}}\right)\mathrm{\mu }\mathrm{m}}{\sqrt{\mathrm{3}}}}=\mathrm{1.0}\mathrm{\mu }\mathrm{m}.$$

The standard uncertainty for the l_wp will be

$$\begin{array}{ll}{\displaystyle }u\left(l_{\mathrm{wp}}\right)& {\displaystyle }=\sqrt{u^{\mathrm{2}}\left(\stackrel{\mathrm{‾}}{l_{\mathrm{wp}}}\right)+u^{\mathrm{2}}\left(l_{\mathrm{wp}}^{\mathrm{mi}}\right)}\\ {\displaystyle }& {\displaystyle }=\sqrt{{\left(\mathrm{0.9}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\left(\mathrm{1.0}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}}=\mathrm{1.4}\mathrm{\mu }\mathrm{m}.\end{array}$$

The standard uncertainty for the value l_rwp can be calculated similarly as for the l_wp:

$$\begin{array}{ll}{\displaystyle }u\left(\stackrel{\mathrm{‾}}{l_{\mathrm{rwp}}}\right)& {\displaystyle }=\sqrt{{\displaystyle \frac{\sum _i^n{\left(l_{{\mathrm{rwp}}_i}-l_{\mathrm{rwp}}\right)}^{\mathrm{2}}}{n-\mathrm{1}}}}=\mathrm{0.6}\mathrm{\mu }\mathrm{m},\\ {\displaystyle }u\left(l_{\mathrm{rwp}}^{\mathrm{mi}}\right)& {\displaystyle }={\displaystyle \frac{\left(\mathrm{1.5}+\frac{\mathrm{125}}{\mathrm{500}}\right)\mathrm{\mu }\mathrm{m}}{\sqrt{\mathrm{3}}}}=\mathrm{1.0}\mathrm{\mu }\mathrm{m},\\ {\displaystyle }u\left(l_{\mathrm{rwp}}\right)& {\displaystyle }=\sqrt{u^{\mathrm{2}}\left(\stackrel{\mathrm{‾}}{l_{\mathrm{rwp}}}\right)+u^{\mathrm{2}}\left(l_{\mathrm{rwp}}^{\mathrm{mi}}\right)}\\ {\displaystyle }& {\displaystyle }=\sqrt{{\left(\mathrm{0.6}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\left(\mathrm{1.0}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}}=\mathrm{1.2}\mathrm{\mu }\mathrm{m}.\end{array}$$

The reported environmental temperature was ∼35 ^∘C. The temperature at the time of measurements was not recorded. By this, it is assumed that Δt_rwp=15 K (t_rwp=35 ^∘C), and because the RWP, WP and the measuring instrument were in the same chamber, all temperature differences $\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}$, $\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}$ and δt_wp are estimated to be zero. The measurements took around 20 min during which the environmental temperature might have changed by ±2 K. So, taking into account the conditions described above and the expanded uncertainty of the thermometer, which was used for environmental temperature measurements U₉₅=1.0 K (k=2), it is possible to estimate the standard uncertainty as follows:

$$\begin{array}{ll}{\displaystyle }u\left(\stackrel{\mathrm{‾}}{\mathrm{\Delta }{t}_{\mathrm{rwp}}}\right)& {\displaystyle }={\displaystyle \frac{\mathrm{2}\mathrm{K}}{\sqrt{\mathrm{3}}}}=\mathrm{1.2}\mathrm{K},\\ {\displaystyle }u\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}^{\mathrm{mi}}\right)& {\displaystyle }={\displaystyle \frac{U_{\mathrm{95}}}{k}}=\mathrm{0.5}\mathrm{K},\\ {\displaystyle }u\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}\right)& {\displaystyle }=\sqrt{u^{\mathrm{2}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}\right)+u^{\mathrm{2}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}^{\mathrm{mi}}\right)}\\ {\displaystyle }& {\displaystyle }=\sqrt{{\left(\mathrm{1.2}\mathrm{K}\right)}^{\mathrm{2}}+{\left(\mathrm{0.5}\mathrm{K}\right)}^{\mathrm{2}}}=\mathrm{1.3}\mathrm{K}.\end{array}$$

The calibration certificate gives the value of the α_rwp with the distribution range $\pm \mathrm{1}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}$, and because actual value ${\mathit{\alpha }}_{\mathrm{rwp}}^{\mathrm{act}}$ can be anywhere within this range at equal probability, a rectangular law of a random value distribution is to be considered. The standard uncertainty is then

$${\displaystyle }u\left({\mathit{\alpha }}_{\mathrm{rwp}}\right)={\displaystyle \frac{\mathrm{1}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}}{\sqrt{\mathrm{3}}}}=\mathrm{0.6}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}.$$

As was said before, the temperatures of the RWP, WP and the measuring instrument are expected to be equal, but the differences $\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}$, $\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}$ and δt_wp should be within the estimated range ±1.0 K. The standard uncertainty is

$${\displaystyle }u\left(\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\right)=u\left(\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)=u\left(\mathit{\delta }{t}_{\mathrm{wp}}\right)={\displaystyle \frac{\mathrm{1.0}\mathrm{K}}{\sqrt{\mathrm{3}}}}=\mathrm{0.6}\mathrm{K}.$$

Similarly to the speculations regarding α_rwp, the difference δα_wp is estimated to be within the range $\pm \mathrm{1}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}$. The standard uncertainty is then

$${\displaystyle }u\left(\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)={\displaystyle \frac{\mathrm{1}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}}{\sqrt{\mathrm{3}}}}=\mathrm{0.6}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}.$$

Now it is possible to express the combined standard uncertainty $u_{\mathrm{c}}^{\mathrm{2}}\left(l_{\mathrm{20}\mathrm{wp}}\right)$ according to Eq. (18):

$$\begin{array}{ll}{\displaystyle }{u}_{\mathrm{c}}^{\mathrm{2}}\left(l_{\mathrm{20}\mathrm{wp}}\right)& {\displaystyle }={\mathrm{1.0}}^{\mathrm{2}}\cdot {\left(\mathrm{0.1}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\mathrm{1.0}}^{\mathrm{2}}\cdot {\left(\mathrm{1.4}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\left(-\mathrm{1.0}\right)}^{\mathrm{2}}\\ {\displaystyle }& {\displaystyle }\cdot {\left(\mathrm{1.2}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\left(\mathrm{0}\mathrm{mm}{\mathrm{K}}^{-\mathrm{1}}\right)}^{\mathrm{2}}\cdot {\left(\mathrm{1.3}\mathrm{K}\right)}^{\mathrm{2}}\\ {\displaystyle }& {\displaystyle }+{\left(\mathrm{0}\mathrm{mm}\mathrm{K}\right)}^{\mathrm{2}}\cdot {\left(\mathrm{0.6}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}\right)}^{\mathrm{2}}+{\left(\mathrm{1.0}\mathrm{\mu }{\mathrm{mK}}^{-\mathrm{1}}\right)}^{\mathrm{2}}\\ {\displaystyle }& {\displaystyle }\cdot {\left(\mathrm{0.6}\mathrm{K}\right)}^{\mathrm{2}}+{\left(-\mathrm{1.0}\mathrm{\mu }\mathrm{m}{\mathrm{K}}^{-\mathrm{1}}\right)}^{\mathrm{2}}\cdot {\left(\mathrm{0.6}\mathrm{K}\right)}^{\mathrm{2}}\\ {\displaystyle }& {\displaystyle }+{\left(-\mathrm{1.3}\mathrm{mm}{\mathrm{K}}^{-\mathrm{1}}\right)}^{\mathrm{2}}\cdot {\left(\mathrm{0.6}\mathrm{K}\right)}^{\mathrm{2}}+{\left(-\mathrm{1874416.2}\mathrm{\mu }\mathrm{m}\mathrm{K}\right)}^{\mathrm{2}}\\ {\displaystyle }& {\displaystyle }\cdot {\left(\mathrm{0.6}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}\right)}^{\mathrm{2}}\\ {\displaystyle }& {\displaystyle }={\left(\mathrm{0.1}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\left(\mathrm{1.4}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\left(-\mathrm{1.2}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\left(\mathrm{0}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}\\ {\displaystyle }& {\displaystyle }+{\left(\mathrm{0}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\left(\mathrm{0.6}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\left(-\mathrm{0.6}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\left(-\mathrm{0.8}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}\\ {\displaystyle }& {\displaystyle }+{\left(-\mathrm{1.1}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}={\left(\mathrm{6.0}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}.\end{array}$$

The crucial contributors here are the values of l_wp, l_rwp and δα_wp – each of them contributed ≥1 µm. These major contributors in the example are the sources of the uncertainty that come from the measuring instrument and the difference between CTEs of the objects to be measured. So, more accurate and precise results can be obtained using a measuring instrument with a lower uncertainty of measurements and workpieces made of the same material.

Table 1 Uncertainty budget for example 1.

Therefore,

$${\displaystyle }{u}_{\mathrm{c}}\left(l_{\mathrm{20}\mathrm{wp}}\right)=\mathrm{2.5}\mathrm{\mu }\mathrm{m}.$$

Using Eqs. (29) and (30), we can express the final value $l_{\mathrm{20}\mathrm{wp}}^{\mathrm{act}}$ at the level of confidence p=95%:

$${\displaystyle }{U}_p=\mathrm{2}\cdot \mathrm{2.5}\mathrm{\mu }\mathrm{m}=\mathrm{5.0}\mathrm{\mu }\mathrm{m},$$

$${\displaystyle }{l}_{\mathrm{20}\mathrm{wp}}=(\mathrm{125.0005}\pm \mathrm{0.0050})\mathrm{mm}.$$

All calculated results according to Eqs. (18)–(28) are shown in Table 1.

The properties of the WP according to the calibration certificate are $l_{\mathrm{20}\mathrm{wp}}=\left(\mathrm{124.9968}\pm \mathrm{0.0002}\right)\mathrm{mm}$ and ${\mathit{\alpha }}_{\mathrm{wp}}=\left(\mathrm{11.60}\times {\mathrm{10}}^{-\mathrm{6}}\pm \mathrm{1}\times {\mathrm{10}}^{-\mathrm{6}}\right){\mathrm{K}}^{-\mathrm{1}}$ (the gauge blocks are from different manufacturers). Now, the E_n criterion (Wöger, 1999) can be applied to check if the calculated value is compatible with the value given in the certificate (JCGM 200:2012, 2012):

$$\begin{array}{}\text{(31)}& {\displaystyle }{E}_n={\displaystyle \frac{l_{\det }-l_{\mathrm{ref}}}{\sqrt{U_{\det }^{\mathrm{2}}+U_{\mathrm{ref}}^{\mathrm{2}}}}},\end{array}$$

where l_det is the measured result and l_ref is the reference value that compatibility is to be checked with. The values U_det and U_ref are their expanded uncertainties correspondingly.

Compatibility is considered to be confirmed if |E_n|≤1.

In this example l_det and U_det are the values that were determined during the measurements and uncertainty evaluation. The values l_ref and U_ref are given in the certificate. Therefore l_det=125.0005 mm, U_det=0.0050 mm, l_ref=124.9968 mm and U_ref=0.0002 mm. Applying Eq. (31), the criterion is

$$\begin{array}{ll}{\displaystyle }{E}_n& {\displaystyle }={\displaystyle \frac{\mathrm{125.0005}\mathrm{mm}-\mathrm{124.9968}\mathrm{mm}}{\sqrt{{\left(\mathrm{0.0050}\mathrm{mm}\right)}^{\mathrm{2}}+{\left(\mathrm{0.0002}\mathrm{mm}\right)}^{\mathrm{2}}}}}\\ {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathrm{0.0037}\mathrm{mm}}{\mathrm{0.0050}\mathrm{mm}}}\approx \mathrm{0.8}\le \mathrm{1}.\end{array}$$

Technically, the compatibility is confirmed (|E_n|≤1); however, the achieved criterion is very close to its boundary value (at which the compatibility is disproved). Is there any way to make the measured result l_det more reliable? As was stated above, in this example the main uncertainty contributors are l_wp, l_rwp and δα_wp. The first two are due to the measuring instrument and cannot be dramatically affected (unless the measuring instrument is changed for a better one), whereas the last is up to the material of the workpieces to be measured so that it can be greatly reduced.

4.2 Example 2

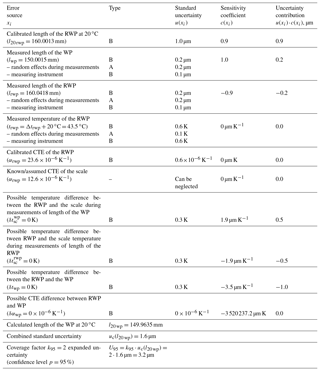
For this example, two actual workpieces are used. They are made of the same material, so now it is known that their CTEs should be completely the same (α_rwp=α_wp). However the workpieces have different shape and length (along the measurement axis). Despite the fact that the workpieces had not been officially calibrated, they were both measured using the CMM at 20 ^∘C multiple times with the uncertainty estimation beforehand so that their geometrical parameters were known and could be checked. The measurements will be made using a length gauge (see Fig. 6).

Figure 6 The reference workpiece (left) and the workpiece (right) and the length gauge in example 2.

The RWP has the following properties: $l_{\mathrm{20}\mathrm{rwp}}=\mathrm{160.0013}\mathrm{mm}\pm \mathrm{0.0020}\mathrm{mm}$ and ${\mathit{\alpha }}_{\mathrm{rwp}}=\mathrm{23.6}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}$.

Measurements that have been carried out give the following values of length of RWP and WP at a current temperature: l_rwp= 160.0418 mm and l_wp= 150.0015 mm.

Using Eq. (13), the desired value can be calculated

$${\displaystyle }{l}_{\mathrm{20}\mathrm{wp}}={\displaystyle \frac{\mathrm{160.0013}\mathrm{mm}\cdot \mathrm{150.0015}\mathrm{mm}}{\mathrm{160.0418}\mathrm{mm}}}=\mathrm{149.9635}\mathrm{mm}.$$

Similar to the first example, we will summarize all known arguments and assume all unknown arguments: l_20 wp=149.9635 mm, l_20 rwp=160.0013 mm, l_wp=150.0015 mm, l_rwp= 160.0418 mm, Δt_rwp=23.5 K, ${\mathit{\alpha }}_{\mathrm{rwp}}=\mathrm{23.6}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}$, ${\mathit{\alpha }}_{\mathrm{sc}}=\mathrm{12.6}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}$, $\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}=\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}=\mathit{\delta }{t}_{\mathrm{wp}}=\mathrm{0}\mathrm{K}$ and $\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}=\mathrm{0}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}$.

In this example the parameter α_sc according to the measuring instrument's manual should be close to zero (made of Zerodur). However, the instrument is mounted on a steel stand which has some nonzero CTE. So the stand's CTE (a table value for steel) was taken as the scale's CTE.

The uncertainty of the l_20 rwp U₉₅=0.0020 mm with coverage factor k=2. The standard uncertainty is then

$${\displaystyle }u\left(l_{\mathrm{20}\mathrm{rwp}}\right)={\displaystyle \frac{U_{\mathrm{95}}}{k}}=\mathrm{0.0010}\mathrm{mm}=\mathrm{1.0}\mathrm{\mu }\mathrm{m}.$$

The value l_wp is achieved as a mean value of six measurements. The standard uncertainty of the measured value can be calculated as a type A standard uncertainty:

$${\displaystyle }u\left(\stackrel{\mathrm{‾}}{l_{\mathrm{wp}}}\right)=\sqrt{{\displaystyle \frac{\sum _i^n{\left(l_{{\mathrm{wp}}_i}-l_{\mathrm{wp}}\right)}^{\mathrm{2}}}{n-\mathrm{1}}}}=\mathrm{0.2}\mathrm{\mu }\mathrm{m}.$$

The calibration certificate for the measuring instrument is not available; the manual states the accuracy of the device to be ±0.2 µm, which we will use as the expanded uncertainty of measurements, and because the actual value $l_{\mathrm{wp}}^{\mathrm{act}}$ can be anywhere within this range at equal probability, a rectangular law of a random value distribution is to be considered. The standard uncertainty due to a random error of the measuring instrument is then

$${\displaystyle }u\left(l_{\mathrm{wp}}^{\mathrm{mi}}\right)={\displaystyle \frac{\mathrm{0.2}\mathrm{\mu }\mathrm{m}}{\sqrt{\mathrm{3}}}}=\mathrm{0.1}\mathrm{\mu }\mathrm{m}.$$

The standard uncertainty for the l_wp will be

$$\begin{array}{ll}{\displaystyle }u\left(l_{\mathrm{wp}}\right)& {\displaystyle }=\sqrt{u^{\mathrm{2}}\left(\stackrel{\mathrm{‾}}{l_{\mathrm{wp}}}\right)+u^{\mathrm{2}}\left(l_{\mathrm{wp}}^{\mathrm{mi}}\right)}\\ {\displaystyle }& {\displaystyle }=\sqrt{{\left(\mathrm{0.2}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\left(\mathrm{0.1}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}}=\mathrm{0.2}\mathrm{\mu }\mathrm{m}.\end{array}$$

The standard uncertainty for the value l_rwp can be calculated similarly as for the l_wp:

$$\begin{array}{ll}{\displaystyle }u\left(\stackrel{\mathrm{‾}}{l_{\mathrm{rwp}}}\right)& {\displaystyle }=\sqrt{{\displaystyle \frac{\sum _i^n{\left(l_{{\mathrm{rwp}}_i}-l_{\mathrm{rwp}}\right)}^{\mathrm{2}}}{n-\mathrm{1}}}}=\mathrm{0.2}\mathrm{\mu }\mathrm{m},\\ {\displaystyle }u\left(l_{\mathrm{rwp}}^{\mathrm{mi}}\right)& {\displaystyle }={\displaystyle \frac{\mathrm{0.2}\mathrm{\mu }\mathrm{m}}{\sqrt{\mathrm{3}}}}=\mathrm{0.1}\mathrm{\mu }\mathrm{m}.\\ {\displaystyle }u\left(l_{\mathrm{rwp}}\right)& {\displaystyle }=\sqrt{u^{\mathrm{2}}\left(\stackrel{\mathrm{‾}}{l_{\mathrm{rwp}}}\right)+u^{\mathrm{2}}\left(l_{\mathrm{rwp}}^{\mathrm{mi}}\right)}\\ {\displaystyle }& {\displaystyle }=\sqrt{{\left(\mathrm{0.1}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\left(\mathrm{0.2}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}}=\mathrm{0.2}\mathrm{\mu }\mathrm{m}.\end{array}$$

The measured environmental temperature was 43–44 ^∘C. The temperature at the time of measurements was not recorded. In this way, it is assumed that Δt_rwp=23.5 K (t_rwp=43.5 ^∘C), and because the RWP, WP and the measuring instrument were in the same chamber, all temperature differences, $\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}$, $\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}$ and δt_wp, are estimated to be zero. The measurements took around 10 min during which the environmental temperature might have changed by ±1 K. So, taking into account the conditions described above and the expanded uncertainty of the thermometer, which was used for the environmental temperature measurements U₉₅=0.1 K (k=2), it is possible to estimate the standard uncertainty as following

$$\begin{array}{ll}{\displaystyle }u\left(\stackrel{\mathrm{‾}}{\mathrm{\Delta }{t}_{\mathrm{rwp}}}\right)& {\displaystyle }={\displaystyle \frac{\mathrm{1}\mathrm{K}}{\sqrt{\mathrm{3}}}}=\mathrm{0.6}\mathrm{K},\\ {\displaystyle }u\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}^{\mathrm{mi}}\right)& {\displaystyle }={\displaystyle \frac{U_{\mathrm{95}}}{k}}=\mathrm{0.1}\mathrm{K},\\ {\displaystyle }u\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}\right)& {\displaystyle }=\sqrt{u^{\mathrm{2}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}\right)+u^{\mathrm{2}}\left(\mathrm{\Delta }{t}_{\mathrm{rwp}}^{\mathrm{mi}}\right)}\\ {\displaystyle }& {\displaystyle }=\sqrt{{\left(\mathrm{0.6}\mathrm{K}\right)}^{\mathrm{2}}+{\left(\mathrm{0.1}\mathrm{K}\right)}^{\mathrm{2}}}=\mathrm{0.6}\mathrm{K}.\end{array}$$

The manufacturer of the aluminium billet (the one that the workpieces are made of) only states the value of the CTE itself without any distribution range; that is why a typical range of $\pm \mathrm{1}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}$ is assumed. Because the actual value ${\mathit{\alpha }}_{\mathrm{rwp}}^{\mathrm{act}}$ can be anywhere within this range at equal probability, a rectangular law of a random value distribution is to be considered. The standard uncertainty is then

$${\displaystyle }u\left({\mathit{\alpha }}_{\mathrm{rwp}}\right)={\displaystyle \frac{\mathrm{1}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}}{\sqrt{\mathrm{3}}}}=\mathrm{0.6}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}.$$

The temperatures of the RWP, WP and the measuring instrument are expected to be equal, but the differences $\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}$, $\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}$ and δt_wp should be within the estimated range ± 0.5 K. The standard uncertainty is

$${\displaystyle }u\left(\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{wp}}\right)=u\left(\mathit{\delta }{t}_{\mathrm{sc}}^{\mathrm{rwp}}\right)=u\left(\mathit{\delta }{t}_{\mathrm{wp}}\right)={\displaystyle \frac{\mathrm{0.5}\mathrm{K}}{\sqrt{\mathrm{3}}}}=\mathrm{0.3}\mathrm{K}.$$

The difference δα_wp is estimated to be $\mathrm{0}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}$. The standard uncertainty is then

$${\displaystyle }u\left(\mathit{\delta }{\mathit{\alpha }}_{\mathrm{wp}}\right)={\displaystyle \frac{\mathrm{0}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}}{\sqrt{\mathrm{3}}}}=\mathrm{0}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}.$$

Now it is possible to express the combined standard uncertainty $u_{\mathrm{c}}^{\mathrm{2}}\left(l_{\mathrm{20}\mathrm{wp}}\right)$ according to Eq. (18):

$$\begin{array}{ll}{\displaystyle }{u}_{\mathrm{c}}^{\mathrm{2}}\left(l_{\mathrm{20}\mathrm{wp}}\right)& {\displaystyle }={\mathrm{0.9}}^{\mathrm{2}}\cdot {\left(\mathrm{1.0}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\mathrm{1.0}}^{\mathrm{2}}\cdot {\left(\mathrm{0.2}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\left(-\mathrm{0.9}\right)}^{\mathrm{2}}\cdot {\left(\mathrm{0.2}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}\\ {\displaystyle }& {\displaystyle }+{\left(\mathrm{0}\mathrm{mm}{\mathrm{K}}^{-\mathrm{1}}\right)}^{\mathrm{2}}\cdot {\left(\mathrm{0.6}\mathrm{K}\right)}^{\mathrm{2}}+{\left(\mathrm{0}\mathrm{mm}\mathrm{K}\right)}^{\mathrm{2}}\cdot {\left(\mathrm{0.6}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}\right)}^{\mathrm{2}}\\ {\displaystyle }& {\displaystyle }+{\left(\mathrm{1.9}\mathrm{\mu }\mathrm{m}{\mathrm{K}}^{-\mathrm{1}}\right)}^{\mathrm{2}}\cdot {\left(\mathrm{0.3}\mathrm{K}\right)}^{\mathrm{2}}\\ {\displaystyle }& {\displaystyle }+{\left(-\mathrm{1.9}\mathrm{\mu }\mathrm{m}{\mathrm{K}}^{-\mathrm{1}}\right)}^{\mathrm{2}}\cdot {\left(\mathrm{0.3}\mathrm{K}\right)}^{\mathrm{2}}+{\left(-\mathrm{3.5}\mathrm{\mu }\mathrm{m}{\mathrm{K}}^{-\mathrm{1}}\right)}^{\mathrm{2}}\\ {\displaystyle }& {\displaystyle }\cdot {\left(\mathrm{0.3}\mathrm{K}\right)}^{\mathrm{2}}+{\left(-\mathrm{3520237.2}\mathrm{\mu }\mathrm{m}\mathrm{K}\right)}^{\mathrm{2}}\cdot {\left(\mathrm{0}\times {\mathrm{10}}^{-\mathrm{6}}{\mathrm{K}}^{-\mathrm{1}}\right)}^{\mathrm{2}}\\ {\displaystyle }& {\displaystyle }={\left(\mathrm{0.9}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\left(\mathrm{0.2}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\left(-\mathrm{0.2}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\left(\mathrm{0}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}\\ {\displaystyle }& {\displaystyle }+{\left(\mathrm{0}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\left(\mathrm{0.5}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\left(-\mathrm{0.5}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}+{\left(-\mathrm{1.0}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}\\ {\displaystyle }& {\displaystyle }+{\left(\mathrm{0}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}={\left(\mathrm{2.4}\mathrm{\mu }\mathrm{m}\right)}^{\mathrm{2}}.\end{array}$$

In this example crucial contributors are only the values of l_20 rwp and δt_wp – each of them contributed ∼1 µm. This means that using a measuring instrument that is even more precise is not profitable. Technically speaking, better accuracy in this case is hardly possible; one of the contributors depends on the accuracy of the RWP's calibration (which is already expected to be higher), and the other on the way that the environmental temperature is distributed. Example 2 shows that the equality of the workpiece's CTEs is much more important than the equality of the geometrical properties.

Table 2 Uncertainty budget for example 2.

Therefore,

$${\displaystyle }{u}_{\mathrm{c}}\left(l_{\mathrm{20}\mathrm{wp}}\right)=\mathrm{1.6}\mathrm{\mu }\mathrm{m}.$$

Using Eqs. (29) and (30), we can express the final value $l_{\mathrm{20}\mathrm{wp}}^{\mathrm{act}}$ at the level of confidence p=95%:

$${\displaystyle }{U}_p=\mathrm{2}\cdot \mathrm{1.6}\mathrm{\mu }\mathrm{m}=\mathrm{3.2}\mathrm{\mu }\mathrm{m},$$

$${\displaystyle }{l}_{\mathrm{20}\mathrm{wp}}=(\mathrm{149.9635}\pm \mathrm{0.0032})\mathrm{mm}.$$

All calculated results are shown in Table 2.

The established length of the WP using precise measurements is $l_{\mathrm{20}\mathrm{wp}}=\mathrm{149.9617}\mathrm{mm}\pm \mathrm{0.0020}\mathrm{mm}$. So, for this example, according to Eq. (31):

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{l}_{\det }=\mathrm{149.9635}\mathrm{mm}\\ {\displaystyle }& {\displaystyle }{U}_{\det }=\mathrm{0.0032}\mathrm{mm}\\ {\displaystyle }& {\displaystyle }{l}_{\mathrm{ref}}=\mathrm{149.9617}\mathrm{mm},\\ {\displaystyle }& {\displaystyle }{U}_{\mathrm{ref}}=\mathrm{0.0020}\mathrm{mm},\\ {\displaystyle }& {\displaystyle }{E}_n={\displaystyle \frac{\mathrm{149.9635}\mathrm{mm}-\mathrm{149.9617}\mathrm{mm}}{\sqrt{{\left(\mathrm{0.0032}\mathrm{mm}\right)}^{\mathrm{2}}+{\left(\mathrm{0.0020}\mathrm{mm}\right)}^{\mathrm{2}}}}}\\ {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathrm{0.0018}\mathrm{mm}}{\mathrm{0.0038}\mathrm{mm}}}\approx \mathrm{0.5}\le \mathrm{1}.\end{array}$$

Here, compatibility is also confirmed. But, in this example, due to a lesser value of E_n, reliability of the determined value l_det (the probability that l_det and l_ref are really compatible) is higher.

The E_n criterion is unfortunately inapplicable for the real measurements as the value l_ref is usually not known. However, the uncertainty contributors' analysis (which for both examples was performed after calculation of the combined standard uncertainty according to Eq. 18) can give enough information about the compatibility of the determined value with some unknown reference value.

Note that all calculations for examples 1 and 2 were performed using MS Excel. Due to a higher accuracy, some of the results might be negligibly different than if they had been obtained using a conventional calculator. The final errors were rounded up (e.g., 2.401 to 2.5 µm).

5 Conclusions

The suggested method does not provide a level of accuracy reachable with methods which require temperature measurements; however, it is universal (can be applied to any linear measuring instrument without any hardware modifications), it does not slow down the measuring process for temperature stabilization (does not create a so-called bottleneck at the production conveyor) and it can be used by a measuring instrument's operator without additional qualification training. The method can be applicable in production areas where no submicron accuracy is required.

The best results are achievable with shortening of the measurements' duration (so the temperature does not change significantly) and the RWP should at least be made of a similar material to the WP. During the measurements, draughts and proximity to warming sources should be avoided (to prevent inequality in the temperature distribution for the RWP and the WP under test).