Calibration of torque measurement under constant rotation in a wind turbine test bench

To determine the efficiency of multi-MW wind turbines, the torque measurement in wind turbine test benches has to be performed with an accuracy better than 0.2 %. To this end, the torque measurement has to be traced to national standards in the MN m range. This can be done by using a novel torque transfer standard in combination with a newly developed torque calibration procedure under constant rotation, which are both presented and discussed in this paper. The calibration procedure was performed on a 4 MW wind turbine test bench and the evaluation of the calibration result, including a measurement uncertainty, is explained in detail.

1 Introduction

Precise torque measurement in multi-MW wind turbine test benches (WTTBs) is crucial for determining the efficiency of wind turbines. However, torque measurement in WTTBs is not yet traceable to national standards due to its enormous magnitude; hence, the measurement uncertainty is not yet known. Moreover, most torque measuring instruments in WTTBs do not measure torque directly at the wind turbine's rotor hub (Zhang and Neshati, 2018), where it is required (Fig. 1). Torque as a mechanical input for a direct efficiency determination is normally to be measured directly at the beginning of the wind turbine's drive train, which is the rotor hub flange. Between the torque measurement (Fig. 1 – torque transducer) and the rotor hub flange, significant losses occur, which have not been fully considered to date.

Common torque calibration standards such as DIN 51309 (09/13) and EURAMET cg-14 (03/2011) provide methods only for static torque calibration. Since both wind turbines and WTTBs operate under rotation, these standards are not simply applicable. Furthermore, in current standards for the certification of wind turbines (Germanischer Lloyd, 2010), the traceability of torque measurement has not yet been incorporated. For that reason, a calibration method for two correlated input variables, torque M and rotational speed n, was developed. To rectify the omission of torque losses along the drive train and enable a traceable torque measurement under rotation directly at the WTTB's rotor hub flange, a 5 MN m torque transducer was acquired and characterized to allow it to be used as a torque transfer standard (TTS). The calibration procedure developed, which is described in Weidinger et al. (2018a), was successfully performed on the WTTB of the Center for Wind Power Drives (CWD) at RWTH Aachen.

Besides the test of the calibration procedure developed and the 5 MN m TTS employed, the torque measurement in the WTTB was traced to the national standard. In this paper, the deviation between the torque measurement in the WTTB and the TTS is calculated including a measurement uncertainty for torque measurement under constant rotational speed based on DIN 7500-1 (05/2014).

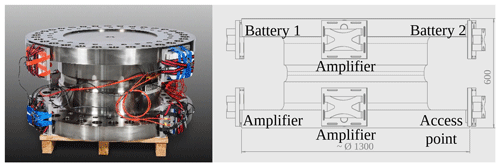
Figure 1 5 MN m TTS, including its data acquisition system (DAQ) and telemetry system, mounted at the rotor hub flange of the wind turbine under test on the WTTB of the Center for Wind Power Drives at RWTH Aachen (edited from Weidinger et al., 2018a).

Figure 2 5 MN m TTS equipped with a self-sufficient DAQ, and a telemetry system to transmit the measurement data in time.

2 The torque transfer standard

The TTS deployed for the calibration is a hollow shaft, multi-component transducer (Fig. 2) based on the strain gauge measuring principle, which can measure loads in all six degrees of freedom. This special transducer has two independent torque measuring bridges M₁ and M₂ and was established as a TTS by calibrating it up to 1.1 MN m at the Physikalisch-Technische Bundesanstalt (PTB). In the following, only measuring bridge M₁ was investigated and used for the torque calibration of the WTTB.

2.1 Telemetry and data acquisition system

To be deployed under rotation, the TTS was equipped with a telemetry system and a transportable DAQ. The DAQ consists of a very precise 225 Hz carrier frequency amplifier (Quantum MX238B) to digitize the two torque measuring bridges and two additional amplifiers (Quantum MX430B) with a carrier frequency of 600 Hz for the other measuring bridges. All amplifiers were synchronized via FireWire using a network time protocol and powered by a battery pack. For a signal transmission in time to surveil the transducer with regard to overload, two access points, which communicated via WLAN, were utilized.

All signals were recorded with a sampling frequency f_sample, which took the maximum rotational speed of the WTTB without torque load (n_max=25 min⁻¹) and the envisioned resolution into account. To achieve a resolution of $r_{\mathrm{rot}}={\mathrm{1}}^{\circ }$ for a maximum rotational speed of n_max=25 min⁻¹, the sampling frequency was calculated to be f_sample=150 Hz by

$$\begin{array}{}\text{(1)}& {\displaystyle }{f}_{\mathrm{sample}}\ge n_{\max }\cdot {\left(r_{\mathrm{rot}}\right)}^{-\mathrm{1}}\cdot {\mathrm{360}}^{\circ }.\end{array}$$

To avoid aliasing effects, the measuring data were filtered using a Bessel filter with an cut-off frequency of f_filter=50 Hz.

The required signal amplifiers, the battery pack, and the access point were distributed symmetrically on the flange of the transfer standard to avoid objectionable torque shunt (Fig. 2).

2.2 Metrological characterization

As mentioned before, the 5 MN m torque transducer was established as a TTS at PTB by statically calibrating it up to 1.1 MN m (Weidinger et al., 2017). Currently, the world's largest torque standard machine (TSM) has a measurement range up to 1.1 MN m and is located at PTB (Peschel et al., 2005). Traceable torque measurement above this range is not possible without a special extrapolation approach (Weidinger et al., 2018c). Due to the purpose of the measurements conducted, a characterization of the TTS above 1.1 MN m is not required here. The coherence between the exactly defined torque M_cal in kN m and the electrical output signal S of the TTS in mV/V up to 1.1 MN m amounts to

$$\begin{array}{}\text{(2)}& {\displaystyle }{M}_{\mathrm{cal}}=\mathrm{3851.5}\mathrm{kN}\mathrm{m}\cdot {\left(\mathrm{mV}/\mathrm{V}\right)}^{-\mathrm{1}}\cdot S.\end{array}$$

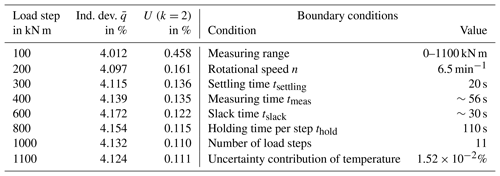
Due to very small non-linearities of ≤0.05 % (Table 1) of the TTS, a linear regression curve for a clockwise torque load and increasing and decreasing steps combined was ascertained. This regression curve was calculated according to DIN 51309 (09/13) case II, where the hysteresis of 0.0539 % is considered in the relative measurement uncertainty. The remaining small non-linearities (Table 1), which are expressed relative to the result at maximum load, are incorporated into the measurement uncertainty in the form of an interpolation deviation. The current drift, the sensitivity deviation over time between the periodically repeated calibrations, of the TTS is given at 0.0089 % and the creep is less than −0.003 %.

Table 1 Metrological parameters of the 5 MN m TTS.

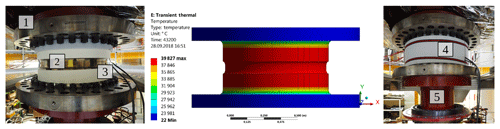
To determine the temperature-dependent sensitivity deviation of the 5 MN m TTS (1) under load, it was calibrated up to 1.1 MN m with a special heating blanket (3) around the hollow shaft as shown in Fig. 3. An insulation (4) was wrapped around the TTS and the heating blanket to heat up the hollow shaft of the TTS when it was installed in the 1.1 MN m TSM (5). During a calibration under normal laboratory conditions, the temperature inside the TTS was 20.85 ^∘C with a fluctuation of < 0.1 K over the entire calibration time. After heating up the TTS for about 12 h, the temperature on the outside surface of the TTS was on average 36.24 ^∘C. This was measured by five Pt100 sensors, which were equally spread and taped around the narrowing of the TTS, as can be seen in Fig. 3 (2). The heating process is simulated in ANSYS by way of illustration as depicted in the middle of Fig. 3. Over the calibration period under elevated temperature, the temperature inside the TTS was 32.77 ^∘C with a stability of 0.1 K.

Since only the air temperature inside the TTS was measured during the WTTB calibration, the temperature-dependent sensitivity alteration for the air temperature inside the TTS is computed. The gap between the temperature in the laboratory and the WTTB accounts for approximately 5 K. Consequently, the temperature dependence of the sensitivity was interpolated to a 5 K difference and amounts to $\mathrm{1.52}\times {\mathrm{10}}^{-\mathrm{2}}$ %. To ensure that the reference conditions of the 1.1 MN m TSM stayed the same for both calibrations, the temperature at the end of the lever arm of the 1.1 MN m TSM and close to the force transducers of the same was recorded and stayed at 21.83 ^∘C with a fluctuation of less than 1 K as required according to DIN 51309 (09/13).

Figure 3 Heat blanket (3) around the 5 MN m TTS (1), which is installed in the 1.1 MN m torque standard machine (5) taped with five Pt100 sensors (2), and isolated by Basotect foam (4).

3 Measurement set-up

For all mechanical systems, efficiency is the ratio between the output and input power, and it can be determined using either an indirect or a direct measurement method. Since an indirect measurement method, as described in Pagitsch et al. (2016), is not feasible for all devices under test, the direct measurement method is favoured. For wind turbines on WTTBs, this means that the mechanical input is to be measured very precisely in the form of rotational speed and torque. To ensure a precise torque measurement, this has to be calibrated. This was done at CWD using the following measurement set-up.

Depending on the objective of the measurements on a WTTB, the targeted measurement uncertainties vary from between 0.1 %–0.2 % for wind turbine and system component efficiency tests, where torque measurement is of great importance, and 2 % for robustness and accelerated life tests for electrical and mechanical components as stated in Kock et al. (2016).

3.1 Wind turbine test bench to be calibrated

The torque transducer in the 4 MW WTTB of CWD is capable of measuring torque up to M_nom=2.7 MN m. As in most WTTBs, in the 4 MW WTTB of CWD the torque is measured between the prime mover and the wind load simulation unit (WLSU) (cf. Fig. 1). This is because of the high loads by the WLSU in the form of additional multi-component loads at the hub flange for full body test modes, which cannot be withstood by most torque transducers and which affect the torque signal.

A torque generation and, therefore, its calibration are not practicable without a device under test. To calibrate the typical operation range of a WTTB, a suitable test object representing frequently tested wind turbines is to be chosen. Here, a 2.75 MW research wind turbine from the Forschungsvereinigung Antriebstechnik e. V. (FVA, 2018) was installed. The FVA wind turbine has a high-speed generator with a main gearbox and was able to withstand torque of M_max=1.6 MN m at the maximum power output under a constant minimum rotation of n_min=6.5 min⁻¹. The TTS was mounted directly at the hub flange of the wind turbine.

The rotational speed n was measured by an incremental encoder with a minimum step of $n_{\mathrm{step},\min }\approx \mathrm{0.1}$ min⁻¹ directly at the motor of the WTTB.

Since the wind turbine was a research object, full access to its control system was provided. For this special set-up, the torque was controlled by the generator converter system based on an additional torque measurement in the lower kN m range on the high-speed shaft in the wind turbine, while the rotational speed was operated by the control system of the prime mover.

3.2 Data synchronization

Because of the autarkic DAQ of the TTS (see Sect. 2.1), two separate DAQs, the DAQ of the WTTB and that of the TTS, were utilized to gather the data of the calibration measurements. In order to evaluate the measurements, the two data sets need to be synchronized in a time-wise manner. This was realized by feeding an ideal square-wave signal with an amplitude of ${\widehat{u}}_{\mathrm{sync}}=\pm \mathrm{5}$ V and a frequency of f_sync=0.2 Hz, which was generated as well as recorded by one of the TTS's amplifiers, into the WTTB's DAQ. Using this easily applicable synchronization signal, the temporal shift between the two data sets was corrected. A more detailed description can be found in Weidinger et al. (2018a).

4 Calibration procedure

The torque calibration procedure developed is based on common static torque standards such as DIN 51309 and EURAMET cg-14. However, these standards apply to static calibrations only and do not consider torque measurement under constant rotation. To remedy this, a new approach for rotary torque calibration was developed that considers general effects as found in reference torque standard machines, to which the present set-up is comparable, and special conditions due to the rotation with the help of Brüge and Pfeiffer (2019).

4.1 Zero signal determination

A crucial parameter for any calibration is the zero-point determination. Its quality and correctness affect all other results of the calibration because of its usage in eliminating the signal offset. A signal offset is caused by pre-tension in the transducer itself and tension created during the assembly process.

As in common calibration standards, the zero signal at the beginning of each load cycle was defined in an unloaded condition (M=0 kN m) but with all electrical components switched on. In the case of a WTTB with a horizontal measuring axis, the zero signal would be distorted by the dead weight influences of the drive train and the transducers themselves. This case does not comply with the operation mode of a WTTB and its torque measurement under rotation. To overcome this issue, a zero signal determination under rotation with the entire measurement set-up was performed.

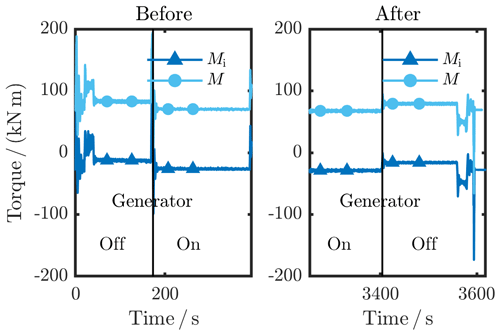
When rotating the drive train with all components connected to each other, torque losses due to friction arise. This can be tackled by switching on the generator control system, which then acts as an additional motor and adjusts the torque to M=0 kN m and, thus, compensates for the friction losses as shown in Fig. 4. All measurement signals were recorded continuously during the calibration process. To determine the zero signal S_zero,rot, the signal was averaged over six full rotations (Eq. 3) with a prior settling time of t_settling=20 s to minimize control effects on the signal (Weidinger et al., 2018a). The zero signal was then used to tare the measurement signal in the following load cycle in post-processing; an active hard taring of the torque signals via an offset correction must be avoided during or after the calibration measurements since it would make the calibration invalid. In Fig. 4, the blue curve represents the torque measured by the WTTB transducer M_i, while the light blue curve depicts the TTS reference torque M.

$$\begin{array}{}\text{(3)}& {\displaystyle }& {\displaystyle }{S}_{\mathrm{zero},\mathrm{rot}}={\displaystyle \frac{\mathrm{1}}{m}}\sum _{i=\mathrm{1}}^m{S}_i\text{(4)}& {\displaystyle }& {\displaystyle }\mathrm{with}m={\displaystyle \frac{l}{n_{\mathrm{WTTB}}\cdot \mathrm{1}\min \cdot {\left(\mathrm{60}\mathrm{s}\right)}^{-\mathrm{1}}}}\cdot f_{\mathrm{sample}}\text{(5)}& {\displaystyle }& {\displaystyle }\mathrm{and}l\in {\mathbb{Z}}_{>\mathrm{0}},\mathrm{here}l=\mathrm{6}.\end{array}$$

Figure 4 Zero signal determination under constant minimum rotation before and after each load cycle.

4.2 Load cycle

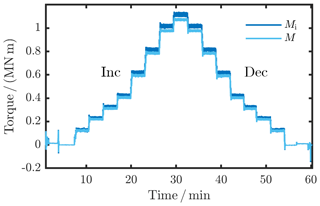
To investigate the calibration approach and to compare it to a static torque calibration, the torque calibration in a WTTB was conducted under a constant rotation of n_const=6.5 min⁻¹. For an easy comparison with the static torque calibration of the TTS itself, the load cycle in the WTTB (Fig. 5) was adjusted to the load cycle of the TTS calibration: stepwise torque application increasingly (inc) and decreasingly (dec) up to 1.1 MN m in a clockwise manner from the prime mover's point of view. The distribution of the load steps matches the torque steps applied for the static calibration of the TTS. The torque signals S_i (cf. Eq. 3) were again averaged over six full rotations after reaching the desired torque value and holding it for t_settling=20 s to reach a stationary state. To determine the repeatability of the torque calibration, the load cycle was repeated four times.

Figure 5 Tared measurement data of a load cycle with stepwise increasing (inc) and decreasing (dec) torque from 0 MN m up to 1.1 MN m.

5 Calibration result

Based on DIN 7500-1 (05/2014), which describes the calibration of force measurement in material testing machines, this torque calibration under constant rotation was evaluated. What is exceptional for DIN 7500-1 (05/2014) is that the load steps do not have to be met exactly in order to calculate a regression curve as the calibration result. Instead, an indication deviation between the signal to be calibrated M_i and the reference signal coming from the TTS M is defined. The calibration result of the torque calibration in the WTTB consists of

• the relative indication deviation q, and

• the measurement uncertainty u_c for q.

Other than constituted in DIN 7500-1 (05/2014), here, the calibration result is not a classification of the transducer calibrated. In agreement with WTTB operators, the calibration result is depicted in the form of

• a look-up table (to correct the result by consulting the table),

• a regression curve (to correct the result in post-processing), or

• a correction of the underlying regression curve of the transducer to be calibrated, which requires a second calibration using the corrected regression curve to determine the measurement uncertainty for the torque measurement in the WTTB.

5.1 Relative indication deviation

The indication deviation is calculated relative to the corresponding load step M_L (relative indication deviation $\overline{q}$) and separately for each load cycle j. It is the deviation between the tared torque signal M_i measured by the WTTB transducer and the tared reference torque signal M given by the TTS:

$$\begin{array}{}\text{(6)}& {\displaystyle }{q}_j\left(M_{\mathrm{L}}\right)={\displaystyle \frac{M_{\text{i},j}\left(M_{\mathrm{L}}\right)-M_j\left(M_{\mathrm{L}}\right)}{M_j\left(M_{\mathrm{L}}\right)}}\cdot \mathrm{100}\mathit{\%}.\end{array}$$

The relative indication deviation $\overline{q}$ is computed separately for increasing (up) and decreasing (down) load steps. Thus, a reversibility between the increasing and decreasing torque loads can be determined. In Fig. 6, the relative indication deviation of the stationary torque calibration performed is plotted, where the light blue curves represent q_j of the individual repetitions j, while the red curve depicts the arithmetic mean ${\overline{q}}_{\mathrm{up}/\mathrm{down}}$ of the relative indication deviations per repetition.

The calibration result is represented as a relative indication deviation $\overline{q}$ in Table 3, which is the arithmetic mean of the increasing and decreasing relative indication deviation per repetition q_j for $j=\mathrm{1},\mathrm{\dots },\mathrm{4}$:

$$\begin{array}{}\text{(7)}& {\displaystyle }\overline{q}\left(M_{\mathrm{L}}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}\sum _{j=\mathrm{1}}^{\mathrm{4}}{q}_j\left(M_{\mathrm{L}}\right).\end{array}$$

To make a statement about the repeatability of the measurements, they are to be repeated at least twice. Here, four repetitions were implemented, which was a compromise between the required measurement time and the possibility of a statistical evaluation.

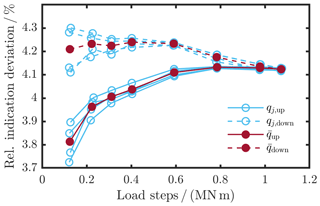
Figure 6 Relative indication deviation of the torque transducer in the WTTB as the result of the torque calibration under a constant rotation of n=6.5 min⁻¹.

The relative repeatability b was defined separately for each load step as the difference between the maximum and minimum relative indication deviations per load step:

$$\begin{array}{}\text{(8)}& {\displaystyle }b\left(M_{\mathrm{L}}\right)=\underset{j}{max}\left(q_j\left(M_{\mathrm{L}}\right)\right)-\underset{j}{min}\left(q_j\left(M_{\mathrm{L}}\right)\right).\end{array}$$

5.2 Relative resolution

In general, the resolution of digital torque signals depends on the resolution of the amplifier's A∕D converter and the data encoding format of the measurement data. For measurements, however, if the indication fluctuation exceeds this resolution, the relative resolution is to be half the span of the indication fluctuation.

According to DIN 7500-1 (05/2014), the indication fluctuation is to be determined with the prime mover and the device under test switched on. In a WTTB under rotation, things are more complicated: eigenfrequencies are to be avoided in general, but eigenfrequencies of higher order were hit and the dead weight of all components has an influence on the measurement as well, which varies under rotation. By averaging the signal over a full rotation, the dead weight effect is corrected for. As the torque signal is averaged over six full rotations, the indication fluctuation is defined as the maximum difference between the six separate mean torque signals per revolution. This indication fluctuation was calculated for each load step and repetition and the maximum was found. Since the resolution of the amplifiers with 16 bits is high and the data save format is sufficient as well, the resolution r here consists merely of half the span of the indication fluctuation, and the relative resolution a per load step was calculated as follows:

$$\begin{array}{}\text{(9)}& {\displaystyle }& {\displaystyle }a\left(M_{\mathrm{L}}\right)={\displaystyle \frac{r\left(M_{\mathrm{L}}\right)}{M\left(M_{\mathrm{L}}\right)}}\cdot \mathrm{100}\mathit{\%},\text{(10)}& {\displaystyle }& {\displaystyle }\mathrm{with}r\left(M_{\mathrm{L}}\right)=\underset{l}{max}\left(r_l\left(M_{\mathrm{L}}\right)\right)-\underset{l}{min}\left(r_l\left(M_{\mathrm{L}}\right)\right)\cdot (\mathrm{2}{)}^{-\mathrm{1}}.\end{array}$$

5.3 Measurement uncertainty

The set-up for calibrating torque measurements in a WTTB by using a TTS is comparable to a reference torque calibration machine. In a reference torque calibration machine, a calibrated and very well-known torque transducer is deployed to calibrate another torque transducer. Due to the resemblance in the set-up, the effects during the calibration are analogous to those found in Röske (2011). The influences on the calibrated torque in the WTTB are listed in Fig. 7 in the form of an Ishikawa diagram, and they are discussed in the following. An Ishikawa diagram is a cause-and-effect diagram to visualize the potential influences on the torque calibration in the WTTB in order to identify their roots.

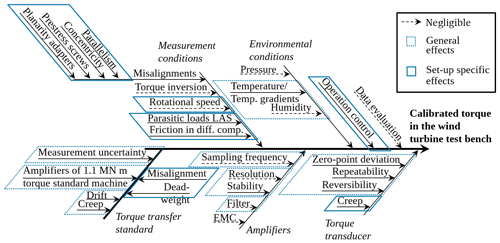
Figure 7 Ishikawa diagram listing the influences on the calibrated torque in the WTTB with the present set-up.

5.3.1 Measurement conditions

The measurement conditions in a set-up to calibrate torque measurement in WTTBs are rather complex (Foyer and Kock, 2017). One important point is misalignments of both transducers, which contain the parallelism, planarity, and concentricity of the adapters, the transducers, and all other components, as well as the prestress of the screws to mount the transducers, and the dead weight. These drive train misalignments cause parasitic loads in the form of forces (F_x, F_y, and F_z) and bending moments (M_y and M_z), which exert an influence on the torque measurement; this effect is called crosstalk (Lietz et al., 2007; Baumgarten et al., 2014). Moreover, the WLSU, which can also simulate wind loads acting at the rotor hub flange, controls these parasitic loads in order to minimize them and to avoid machine vibrations to protect the set-up. A control to zero is not possible because of the control system's inaccuracy. The additional loads due to misalignment and the inaccuracy of the WTTB control system were measured by the TTS during all measurements, and the tared signals can be seen as an example in Fig. 8. The measuring bridges besides the torque measuring bridge are not calibrated; hence, a quantitative evaluation of the additional load effects is not possible. However, the plot shows qualitatively that the additional loads are periodically recurrent and, therefore, they are systematic errors, which were corrected for by averaging all signals over one or a multiple of full revolutions. Furthermore, the additional loads are relatively small, with a superposition of maximum 76.44 and 68.29 kN m for the maximum torque load step.

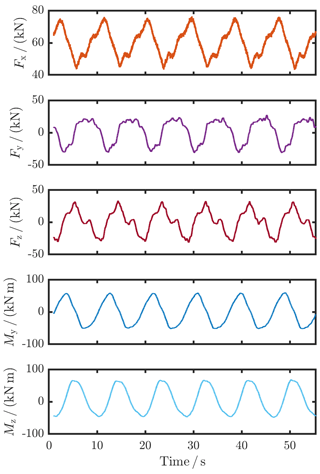
Figure 8 Additional multi-component loads during the calibration measurements due to the inaccuracy of the control system of the WTTB.

In essence, under high rotational speed, the behaviour of a torque transducer can differ from the behaviour under static conditions due to the rotation-induced centripetal force. This can lead to signal alterations; however, as found in Brüge (1997), the relative deviation of the torque signal under a rotation of n=100 min⁻¹ is less than $\mathrm{6}\times {\mathrm{10}}^{-\mathrm{4}}$. Based on this outcome, the influence of the constant rotational speed at n=6.5 min⁻¹ on the TTS and the WTTB transducer is imperceptible for this estimation.

Due to emergency braking, which may occur and which is to be tested under normal testing conditions, torque inversion up to 80 % of the maximum torque applied beforehand is evoked. In the case of emergency braking while performing calibration measurements, the maximum torque load in the driving direction was applied afterwards for about 5 min and a new zero signal was determined. In this way, the hysteresis effect on the torque signal was minimized.

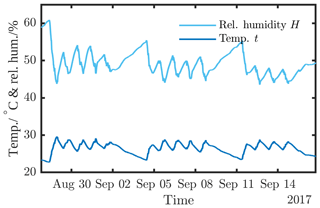
For calibrations in general, environmental conditions such as temperature need to be stable to ±1 K and are supposed to be in the range between 18 and 28 ^∘C (EURAMET cg-14, 03/2011). The humidity influence is negligible at this point, as is the air pressure for strain-gauge-based measurement tools. In WTTBs, the environmental conditions are not stable because of the large volume in the laboratory and the manifold sources of heat like the gearbox, the generator, and the WLSU. For the calibration in the WTTB, the temperature distribution over the TTS was monitored and the temperature difference over the TTS was found to be within $\mathrm{\Delta }{T}_{\mathrm{place}}=\pm \mathrm{1}$ K. Additionally, the temperature inside the hollow shaft of the TTS was recorded permanently. As shown in Fig. 9, the daily temperature difference is $\mathrm{\Delta }{T}_{\mathrm{day}}=\pm \mathrm{2}$ K. However, for a static torque calibration which took about $t_{\mathrm{meas},\mathrm{total}}=\mathrm{60}$ min, the temperature difference is $\mathrm{\Delta }{T}_{\mathrm{loadcycle}}=\pm \mathrm{1}$ K. This is stable enough that no signal correction due to temperature dependence is to be executed. However, the temperature dependence of the TTS sensitivity is to be considered in the measurement uncertainty contribution of the TTS (Sect. 5.3.5).

Figure 9 Temperature and humidity in the TTS during the torque calibration of the WTTB.

5.3.2 Data acquisition evaluation

The data acquisition was chosen in such a way to reduce all effects on the measurement result. All electrical components were heated up prior to the measurements to avoid influences by an unstable condition in the electronics. Moreover, as aforementioned, the sampling frequency was chosen to realize at least a 1^∘ resolution of a full rotation (f_WTTB=1200 Hz and f_TTS=150 Hz). In addition, the filters were set in order to avoid aliasing effects. Other effects of the sampling frequency and the filter settings were not analysed any further.

Due to experiments performed by Thomas Kleckers (personal communication, 2017), it can be concluded that static electromagnetic fields do not have an impact on the measurement signal. Once the operation control process is finished and a stationary state is reached, the electromagnetic field should be static; therefore, the electromagnetic compatibility (EMC) is negligible.

Table 2 Additional contributions to the measurement uncertainty of the TTS.

Moreover, the influence caused by the data evaluation is negligible because of the continuous data recording, a good data synchronization of the two data sets, and precise post-processing using the rotational speed and the data time stamps to average over six full revolutions.

5.3.3 Uncertainty contribution of the resolution

The uncertainty contribution of the relative resolution u_res of the transducer in the WTTB was examined based on DIN 7500-1 (05/2014) for each load step, and it is the square root of the sum of the following components squared:

• the uncertainty component because of the relative resolution of the torque measurement instrument in the test bench under load, which is denoted as a_M divided by $\mathrm{2}\sqrt{\mathrm{3}}$ because of the assumption of a rectangular distribution, and

• the uncertainty component because of the relative resolution of the torque measurement instrument in the test bench after load release, which is denoted as a_Z divided by $\mathrm{2}\sqrt{\mathrm{3}}$ (same assumption of a rectangular distribution). The relative resolution of the torque measurement after load release is part of the indication deviation of every load step because of the aforementioned taring of the torque values for every load step.

The uncertainty contribution of the relative resolution u_res was calculated for every load step as follows:

$$\begin{array}{}\text{(11)}& {\displaystyle }{u}_{\mathrm{res}}\left(M_{\mathrm{L}}\right)=\sqrt{{\left({\displaystyle \frac{a_M\left(M_{\mathrm{L}}\right)}{\mathrm{2}\sqrt{\mathrm{3}}}}\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{a_Z}{\mathrm{2}\sqrt{\mathrm{3}}}}\right)}^{\mathrm{2}}}.\end{array}$$

Table 3 Expanded (k=2) absolute measurement uncertainty U for the best expected value for the mean relative indication deviation $\overline{q}$ and overview of the prevailing boundary conditions during the calibration.

5.3.4 Uncertainty contribution of the repeatability

Furthermore, the relative repeatability is considered an uncertainty contribution, too. The uncertainty contribution of the relative repeatability u_rep referring to DIN 7500-1 (05/2014) is the standard deviation of the best expected value q_j in % and the relative mean indication deviation $\overline{q}$ in %, where j are the repetitions per load step (here $j=\mathrm{1},\mathrm{\dots },\mathrm{4}$):

$$\begin{array}{}\text{(12)}& {\displaystyle }{u}_{\mathrm{rep}}\left(M_{\mathrm{L}}\right)=\sqrt{{\displaystyle \frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{4}-\mathrm{1}\right)}}\sum _{j=\mathrm{1}}^{\mathrm{4}}{\left(q_j\left(M_{\mathrm{L}}\right)-\overline{q}\left(M_{\mathrm{L}}\right)\right)}^{\mathrm{2}}}.\end{array}$$

5.3.5 Uncertainty contribution of the torque transfer standard

As the last contribution to the total measurement uncertainty, the relative measurement uncertainty of the TTS u_std was considered. This consists of the relative measurement uncertainty of the metrological properties of the TTS u_cal, which are stated in the calibration certificate of the TTS, and additional possible uncertainty contributions (A, B, and C):

$$\begin{array}{}\text{(13)}& {\displaystyle }{u}_{\mathrm{std}}\left(M_{\mathrm{L}}\right)=\sqrt{{\left(u_{\mathrm{cal}}\left(M_{\mathrm{L}}\right)\right)}^{\mathrm{2}}+{\mathrm{A}}^{\mathrm{2}}+{\mathrm{B}}^{\mathrm{2}}+{\mathrm{C}}^{\mathrm{2}}}.\end{array}$$

Since the TTS itself was not calibrated using the same measuring chain as when deployed in the WTTB, the calibration of the amplifiers used was taken into account. As this is a matter of a systematic error, the torque signal from the TTS was corrected for the amplifier exchange; the raw torque signal was revised by the relative deviations of the amplifier used for the WTTB calibration and corrected for the relative deviations of the amplifier deployed for the calibration of the TTS itself. The uncertainty of the amplifier calibration is considered as an additional uncertainty contribution A (cf. Table 2).

Another contribution to the measurement uncertainty is the relative drift of the TTS sensitivity over time. This drift was determined by calibrating the TTS before and after the calibration in the WTTB and is considered uncertainty contribution B (cf. Table 2).

The temperature during the calibration in the WTTB deviated from the temperature during the calibration of the TTS. Even though the temperature in the WTTB was not stable, the temperature-dependent sensitivity alteration per 5 K was regarded in the measurement uncertainty as contribution C.

5.3.6 Expected value for the indication deviation

The result of the torque calibration is the best expected value for the mean relative indication deviation $\overline{q}$ of the torque transducer in the WTTB. Moreover, an expanded absolute measurement uncertainty U belongs to this relative indication deviation, which is the product of the coverage factor k and the combined absolute uncertainty u_c of all uncertainty contributions:

$$\begin{array}{}\text{(14)}& {\displaystyle }U\left(M_{\mathrm{L}}\right)& {\displaystyle }=k\cdot u_{\mathrm{c}}\left(M_{\mathrm{L}}\right)=k\cdot \sqrt{\sum _{j=\mathrm{1}}^{\mathrm{4}}{\left(u_j\left(M_{\mathrm{L}}\right)\right)}^{\mathrm{2}}}\text{(15)}& {\displaystyle }& {\displaystyle }=k\cdot \sqrt{{\left(u_{\mathrm{res}}\left(M_{\mathrm{L}}\right)\right)}^{\mathrm{2}}+{\left(u_{\mathrm{rep}}\left(M_{\mathrm{L}}\right)\right)}^{\mathrm{2}}+{\left(u_{\mathrm{std}}\left(M_{\mathrm{L}}\right)\right)}^{\mathrm{2}}}.\end{array}$$

As recommended, a coverage factor of k=2 was used.

The stepwise results, both the mean relative indication deviation $\overline{q}$ and the expanded absolute measurement uncertainty U (k=2), are given in Table 3. As expected, the measurement uncertainty is larger for smaller torque steps due to the worse signal-to-noise ratio, the poorer resolution, and the worse repeatability in this small measurement range. The hysteresis highly depends on the maximum torque applied and is, therefore, not observed here. Instead, the relative indication deviation was averaged over increasing and decreasing torque loads and the measurement uncertainty was determined for the mean $\overline{q}\left(M_{\mathrm{L}}\right)$.

6 Conclusions

This paper introduces the calibration of torque measurement under constant rotation in a WTTB, which was performed for the first time. The torque was applied stepwise between 100 kN m and 1.1 MN m. As a result of the calibration, the mean relative indication deviation $\overline{q}$ between the reference torque, which was measured by the TTS, and the torque recorded by the torque transducer in the WTTB was calculated. This mean relative indication deviation amounts to ≈4 % for the WTTB of CWD at RWTH Aachen. Moreover, as part of the calibration result, an absolute measurement uncertainty consisting of the uncertainty contributions of the relative resolution, the relative repeatability, and the relative measurement uncertainty of the TTS was calculated. With an expanded absolute measurement uncertainty U(M_L) of ≤0.161 % of the mean relative indication deviation $\overline{q}\left(M_{\mathrm{L}}\right)$, the goal of a measurement uncertainty of ≤0.2 % was achieved except for the smallest load step. For the smallest load step, influences like the relative resolution with an uncertainty contribution of u_res(100 kN m)=0.211 % (u_res(1.1 MN m)=0.029 %), the relative repeatability with an uncertainty contribution of u_rep(100 kN m)=0.044 % (u_rep(1.1 MN m)=0.003 %), and a worse signal-to-noise ratio are major factors in the calculation of the total expanded measurement uncertainty.

The torque measurement under constant minimum rotation n_min=6.5 min⁻¹ in the WTTB of CWD at RWTH Aachen is now traced to the national standard in the range between 100 kN m and 1.1 MN m. In addition, with an expanded measurement uncertainty of ≤0.161 % of the relative indication deviation, the torque measurement is precise enough for an efficiency determination of devices under test in the WTTB.

However, since WTTBs work not only under constant rotation, but also under varying rotational speed, the torque measurement should be calibrated under varying rotational speed as well.