Homogenous nuclear magnetic resonance probe using the space harmonics suppression method

Nuclear magnetic resonance imaging (MRI) has became an unavoidable medical tool in spite of its poor sensitivity. This fact motivates the efforts to enhance the nuclear magnetic resonance (NMR) probe performance. Thus, the nuclear spin excitation and detection, classically performed using radio-frequency coils, are required to be highly sensitive and homogeneous. The space harmonics suppression (SHS) method, already demonstrated to construct coil producing homogenous static magnetic field, is used in this work to design radio-frequency coils. The SHS method is used to determine the distribution of the electrical conductive wires which are organized in a saddle-coil-like configuration. The theoretical study of these SHS coils allows one to expect an enhancement of the signal-to-noise ratio with respect to saddle coil. Coils prototypes were constructed and tested to measure ¹H NMR signal at a low magnetic field (8 mT) and perform MRI acquired at a high magnetic field (3 T). The signal-to-noise ratios of these SHS coils are compared to the one of saddle coil and birdcage (in the 3 T case) of the same size under the same pulse sequence conditions demonstrating the performance enhancement allowed by the SHS coils.

1 Introduction

When nuclei having a nuclear spin are immersed in a magnetic field (B₀), an aligned magnetization (M), resulting from the balance between parallel and anti-parallel magnetic moments, occurs. Besides this net magnetization, the nuclear spins precess at the Larmor angular frequency: ${\mathit{\omega }}_{\mathrm{0}}=-\mathit{\gamma }{B}_{\mathrm{0}}$, where γ is the gyromagnetic ratio of a given nucleus. The nuclear spin is disturbed by applying a weak radio-frequency magnetic field B₁ at the Larmor frequency. Thus, the magnetization (M) is tilted, offering the possibility to detect the electromagnetic field associated with the precession and return to the thermal equilibrium (Bloch, 1946). The excitation and detection of the nuclear spins are usually performed using radio-frequency (RF) coils, also referred to as NMR/MRI (nuclear magnetic resonance/magnetic resonance imaging) probes. High signal-to-noise ratio (SNR) and homogeneity remain the main desirable features of these NMR/MRI probes. Research in this area remains active, and various MRI probe configurations have been proposed to address this need (Mispelter et al., 2006): solenoid, saddle coil, birdcage, Bolinger coil, etc.

2 NMR probe overview

At the beginning of NMR history, saddle coil was generalized in NMR experiment because of its homogeneity and its convenience, especially the sample arrangement inside the coil (Hoult and Richards, 1976). A very important enhancement of RF coil was then proposed by Hayes et al. (1985) through the birdcage resonator. This resonator takes advantage of the cosine current density distribution, known to promote magnetic field homogeneity, by means of capacitors producing a phase shift of the current along the circumference. Another type of MRI cosine coil, inspired from older work (Clarck, 1938), was proposed in Bolinger et al. (1988). It consisted in approaching the cosine current distribution by positioning the electrical conductor along the circumference of a circle following a geometric rule (i.e., an equal distance of the conductor projection along the diameter circle). It was recently proposed to enhance the magnetic field homogeneity of the Bolinger coil by means of the space harmonics suppression (SHS) method (Coillot et al., 2016a). The efficiency of the SHS method was demonstrated thanks to numerical finite element method analysis. SHS method was then extended to enhance the homogeneity of the coils by adjusting both the angular position of the wires (distributed along the circle circumference) and the current magnitude flowing through the wires (Sidi-Boulenouar et al., 2018). The extended method efficiency was illustrated through the realization of a spherical shape distributed coils creating a highly homogenous static magnetic field for NMR device. This work concerns the fabrication of a radio-frequency coils for NMR and MRI based on SHS method in axisymmetric case for a finite-size geometry.

3 Study of saddle-like SHS coil

The SHS coil, as depicted on the left-hand side of Fig. 1, consists in N pair of coils represented by distributed electrical conductors along z axis. For instance, the nth coil will consist of four wires located at θ_n angular positions from either side of the x axis. Each coil owns N_n conductors flown by a current i_n. Thus, the nth coil will be represented by its ampere-turn number expressed as I_n=N_ni_n. The θ_n angular positions, enhancing the magnetic field coil homogeneity, are determined by applying the SHS method. The turns are then closed by connecting the electrical conductors through arc portions on the upper and lower parts forming the so-called “saddle-like SHS coil', as illustrated on the right-hand side of Fig. 1) for two pairs of coils. In the following, we will focus on the performance of the saddle-like SHS coils in terms of sensitivity and SNR, the homogeneity of SHS coils having been discussed in previous works.

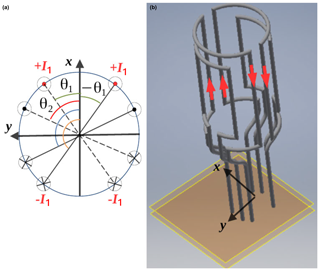
Figure 1 (a) Electrical conductors of angular positions (θ), flown by currents I_n, are distributed along the circumference. (b) Illustration of a saddle-like SHS coil with two pairs of coils.

3.1 Sensitivity of saddle-like SHS coil

From Biot–Savart law the magnetic field contribution for the four wires of the nth coil can be determined. We assume that the straight conductors forming the coil have a height L. They are located at a distance R to the z axis, at an angular position θ_n from either side of the x axis and are flown by a current I_n. The current flowing through these four wires will produce magnetic field contribution (B_wire) in the y-axis direction, given by Eq. (1). The details of the calculation are reported in Appendix A.

$$\begin{array}{}\text{(1)}& {\mathrm{Bwire}}_n(\mathrm{0},\mathrm{0},\mathrm{0})={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}{I}_n}{\mathit{\pi }R}}{\displaystyle \frac{L}{\sqrt{R^{\mathrm{2}}+(L/\mathrm{2}{)}^{\mathrm{2}}}}}\cos \left({\mathit{\theta }}_n\right)\end{array}$$

Next, the magnetic field contribution (at the coil center) of the arc portion (Barc_n) in the y-axis direction is given by Eq. (2). The details of the calculation are reported in Appendix A.

$$\begin{array}{}\text{(2)}& {\mathrm{Barc}}_n(\mathrm{0},\mathrm{0},\mathrm{0})={\displaystyle \frac{\mathrm{2}{\mathit{\mu }}_{\mathrm{0}}RL{I}_n}{(R^{\mathrm{2}}+(L/\mathrm{2}{)}^{\mathrm{2}}{)}^{\mathrm{3}/\mathrm{2}}}}\cos \left({\mathit{\theta }}_n\right)\end{array}$$

Consequently, the total field at the center $(B_{\mathrm{SHS}}={\mathrm{\Sigma }}_{n=\mathrm{1}}^N({\mathrm{Bwire}}_n(\mathrm{0},\mathrm{0},\mathrm{0})+{\mathrm{Barc}}_n(\mathrm{0},\mathrm{0},\mathrm{0}))$ in the y-axis direction) produced by the N pairs of coils of the saddle-like SHS coil will be

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{B}_{\mathrm{SHS}}& ={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}L}{\sqrt{R^{\mathrm{2}}+(L/\mathrm{2}{)}^{\mathrm{2}}}}}\left({\displaystyle \frac{\mathrm{1}}{\mathit{\pi }R}}+{\displaystyle \frac{\mathrm{2}R}{R^{\mathrm{2}}+(L/\mathrm{2}{)}^{\mathrm{2}}}}\right)\\ & {\mathrm{\Sigma }}_{n=\mathrm{1}}^N{I}_n\cos \left({\mathit{\theta }}_n\right).\end{array}\end{array}$$

Lastly, by assuming that coils are flown by identical currents ($I=I_n\forall n$), the coil sensitivity ($S_{\mathrm{coil}}=B_{\mathrm{SHS}}/I$, cf. Hoult and Richards, 1976) can be written as

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{S}_{\mathrm{coil}}& \propto {\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}L}{\sqrt{R^{\mathrm{2}}+(L/\mathrm{2}{)}^{\mathrm{2}}}}}\left({\displaystyle \frac{\mathrm{1}}{\mathit{\pi }R}}+{\displaystyle \frac{\mathrm{2}R}{R^{\mathrm{2}}+(L/\mathrm{2}{)}^{\mathrm{2}}}}\right)\\ & {\mathrm{\Sigma }}_{n=\mathrm{1}}^N\cos \left({\mathit{\theta }}_n\right).\end{array}\end{array}$$

Consequently, the induced voltage (e(t)), using Hoult formula, is expressed as

$$\begin{array}{}\text{(5)}& e\left(t\right)=-S_{\mathrm{coil}}{\displaystyle \frac{\partial \mathit{\delta }{m}_{xy}\left(t\right)}{\partial t}},\end{array}$$

where δm_xy(t) is the magnetic moment in x–y plane and S_coil is the coil sensitivity factor given by Eq. (4). Since the magnetic moment in x–y plane precesses at Larmor angular frequency ω₀, the induced voltage becomes Eq. (6):

$$\begin{array}{}\text{(6)}& \mathrm{|}e\left(j{\mathit{\omega }}_{\mathrm{0}}\right)\mathrm{|}=S_{\mathrm{coil}}{\mathit{\omega }}_{\mathrm{0}}\mathit{\delta }{m}_{xy}.\end{array}$$

3.2 Signal-to-noise ratio of saddle-like SHS coil

In this section we will focus on the intrinsic SNR of the SHS coil. We assume round wires and a strong skin effect regime (i.e., skin depth δ much smaller than wire radius); we neglect the proximity effect occurring between closed conductors. Under these approximations, the equivalent copper section of the wire is approximated by S_wire=2πr_wδ, where r_w is the conductor wire radius. On the other side the length of the coil conductor is expressed as $L_{\mathrm{coil}}=\mathrm{4}(L+R\times (\mathit{\pi }-\mathrm{2}{\mathit{\theta }}_n\left)\right)$. Thus, the electrical resistance of the nth pair of coils (Res_n), forming an angle θ_n, is written as

$$\begin{array}{}\text{(7)}& {\mathrm{Res}}_n={\displaystyle \frac{\mathrm{2}\mathit{\rho }(L+R\times (\mathit{\pi }-\mathrm{2}{\mathit{\theta }}_n\left)\right)}{\mathit{\pi }{r}_{\mathrm{w}}\mathit{\delta }}},\end{array}$$

where ρ is the conductor material resistivity and $\mathit{\delta }=\sqrt{\mathrm{2}\mathit{\rho }/\mathit{\mu }\mathit{\omega }}$ is the skin depth (μ is the magnetic permeability and ω is the pulsation). Assuming the coils are connected in series, the total resistance (Res) will be the sum of each pair of coil resistance. We then deduced from Eq. (7) the total resistance equation:

$$\begin{array}{}\text{(8)}& \mathrm{Res}={\mathrm{\Sigma }}_{n=\mathrm{1}}^{N}Re{s}_n={\displaystyle \frac{\mathrm{2}N\mathit{\rho }}{\mathit{\pi }{r}_{\mathrm{w}}\mathit{\delta }}}(L+R\times (\mathit{\pi }-\mathrm{2}{\mathrm{\Sigma }}_{n=\mathrm{1}}^N{\mathit{\theta }}_n/N\left)\right).\end{array}$$

Lastly, by assuming a main noise contribution due to Johnson–Nyquist noise (i.e., whose power spectrum density is expressed 4kTRes, where k is the Boltzmann constant and T the temperature in K), the rms voltage noise (v_n) of the coil over a frequency range (BW) is deduced from Wiener–Khinchin theorem application (Khintchine, 1934):

$$\begin{array}{}\text{(9)}& v_{\mathrm{n}}=\sqrt{\mathrm{4}\mathrm{kTRes}\times \mathrm{BW}}.\end{array}$$

The intrinsic signal-to-noise ratio (SNR) is defined as

$$\begin{array}{}\text{(10)}& \mathrm{SNR}={\displaystyle \frac{\mathrm{|}e\left(j{\mathit{\omega }}_{\mathrm{0}}\right)\mathrm{|}}{v_{\mathrm{n}}}}.\end{array}$$

Thus, the SNR of the coil is deduced except for a factor, by combining induced voltage (Eq. 6) and the rms voltage noise (Eq. 9):

$$\begin{array}{}\text{(11)}& \mathrm{SNR}\propto {\displaystyle \frac{\mathit{\delta }m}{\sqrt{N}}}{\displaystyle \frac{{\mathrm{\Sigma }}_{n=\mathrm{1}}^N\cos \left({\mathit{\theta }}_n\right)}{\sqrt{L+R(\mathit{\pi }-\mathrm{2}{\mathrm{\Sigma }}_{n=\mathrm{1}}^N{\mathit{\theta }}_n/N)}}}.\end{array}$$

The SNR improvement can then be appreciated by comparing the SHS4 and SHS6 coils SNR to the one of SHS2 (i.e., the saddle coil). For this purpose, we will consider the angle values for one, two and three pairs of coils obtained by the SHS method (Coillot et al., 2016a) and reiterated here:

• SHS2 (1 pair): ${\mathit{\theta }}_{\mathrm{1}}={\mathrm{30}}^{\circ }$

• SHS4 (2 pairs): ${\mathit{\theta }}_{\mathrm{1}}={\mathrm{12}}^{\circ }$ and ${\mathit{\theta }}_{\mathrm{2}}={\mathrm{48}}^{\circ }$

• SHS6 (3 pairs): ${\mathit{\theta }}_{\mathrm{1}}={\mathrm{11.56}}^{\circ }$, ${\mathit{\theta }}_{\mathrm{2}}={\mathrm{26}}^{\circ }$ and ${\mathit{\theta }}_{\mathrm{3}}={\mathrm{56}}^{\circ }$.

We assume the height-to-radius ratio known to optimize the sensitivity of the saddle coil (i.e., $L=\mathrm{2}R\sqrt{\mathrm{2}}$; see Mispelter et al., 2006). In this case, the normalized SNR value estimation (reported in Table 1) shows a significant enhancement for SHS4 and SHS6 with respect to the conventional SHS2 (formal saddle coil).

Table 1 Comparison of coil sensitivities obtained by numerical simulation versus coil sensitivities and SNR deduced from the analytic model. The obtained sensitivities and SNR values are normalized with respect to the SHS2 coil.

4 SHS coils prototypes: designs and experimental results

Various SHS coils are customized in our laboratory, at two extreme frequencies 336 kHz and 128 MHz (corresponding to the ¹H Larmor frequency under respectively 8 mT NMR and 3 T MRI) in order to compare their performances in terms of SNR and magnetic field homogeneity (at least for the 3 T MRI case).

4.1 SHS coils at low magnetic field (8 mT)

In the context of a low magnetic field NMR dedicated to agronomic studies in planta (Sidi-Boulenouar et al., 2018), we have designed two SHS coils, referred to as SHS2 and SHS6 (see Fig. 2). The size and geometry of the coils were imposed by the context of the agronomic study: measurements on a sorghum stem. That led us to choose a 30 mm diameter and 40 mm height coil. For practical reasons we used 0.5 mm diameter insulated copper wire as a compromise between the need of high diameter wire (to reduce thermal noise) and the mechanical constraints (flexibility for the winding feasibility). Lastly, the turn number (120 turns, dispatched in three pairs of coils for SHS6) was chosen to get a self-resonance frequency of each coil closed to the ¹H Larmor frequency. These coils have the particularity to be clampable in order to manage both the integrity of the plant and the versatility of the NMR instrument.

The measured quality factor of the SHS2 and SHS6 coils were respectively 40 and 80. The SNR of a NMR experiment performed on a same water sample (4 cm³ volume) under the same pulse condition has exhibited a factor of 3 enhancement between the two SHS coils. The details of the testing conditions are reported in Sidi-Boulenouar (2018b). This SNR enhancement, in favor of the SHS6 coil, is slightly higher than the expected one (cf. Table 1). This enhancement could be a consequence of the expected homogeneity improvement since the quantity of magnetization measurable is related to the RF field homogeneity.

Figure 2 SHS clampable coils dedicated to the low-field NMR (8 mT) device. Their resonant frequency was tuned closed to 336 kHz (corresponding to the ¹H Larmor frequency at 8 mT). Right figure represents the SHS2 clampable coil and left figure the SHS6. The supporting structure has been realized by 3D printing.

4.2 SHS coils at high magnetic field (3 T)

4.2.1 Experimental setup

A small animal 3 T MRI from RS²D company was used. The ¹H resonant frequency into this 3 T MRI is 128 MHz. The reference MRI probe consists in a quadrature decoupled birdcage (from MRI Tools company) whose dimensions are as follows: coil length =80 mm and inner diameter =42 mm. The outer tube diameter is =99 mm in order to guide the antenna into the 100 mm diameter tunnel of the MRI. Birdcage probe and SHS coils used at 3 T were fed through a power splitter device. All the SHS coils were prototyped for the purpose of the study within our lab. The same device was used for both coils.

4.2.2 SHS4 coil 3 T prototype

At higher frequency, MRI probe designer must take care that the coil length remains smaller than a fraction of the wavelength ($\sim \mathrm{1}/\mathrm{10}$) at the frequency of interest. When this is not the case, the MRI coil must be segmented (Mispelter et al., 2006) to ensure that the quasi-static magnetic field hypothesis is suitable. For the high field condition (i.e., implying high frequency operating), the coil wire of the SHS coil must be segmented as illustrated in Fig. 3.

.

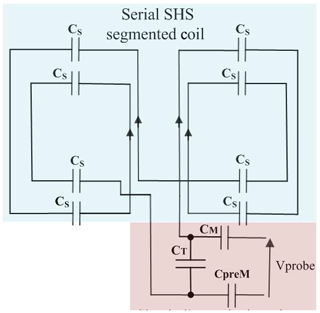
Figure 3 Electrical circuit of the segmented SHS4 coil (3 T prototype) with tuning–matching circuit: C_S is a fixed segmentation capacitance, C_T is a variable capacitance, C_preM is a fixed matching capacitance and C_M is a variable capacitance allowing to match finely the impedance of the coil near the Larmor frequency

Finally, a quadrature-driven SHS4 coil prototype (illustrated in Fig. 4), dedicated to 1H measuring in a small-animal 3 T MRI, has been constructed. Its dimensions were chosen identical to the ones of the reference birdcage given above. The coil itself is realized on a flexible printed circuit board with a copper ribbon width equal to 3 mm. The flexible circuit includes pads to welcome the segmentation capacitors. To allow the quadrature driving, two identical flexible circuits were used. Each flexible circuit was associated with its own tuning and matching circuit (whose configuration circuit is similar to the one presented in Coillot et al., 2016b). The segmented capacitance values of the prototypes are experimentally determined to coincide with the electrical resonance and Larmor frequencies. For the SHS 6 prototype C_S=44 pF was chosen and the coil was divided into 4 segments of length ∼25 cm in order to equalize with electrical resonance frequency to the Larmor one. C_T, C_M and C_preM are respectively the tuning, matching and “pre-matching capacitances. C_T and C_M are non-magnetic variable capacitances from VOLTRONICS, while C_S and C_preM are non-magnetic fixed capacitances from TEMEX.

Figure 4 Quadrature SHS4 serial coil dedicated to ¹H 3 T MRI (80 mm length and 42 mm internal diameter). The coils are realized on a same flexible printed circuit board including the pads to welcome the segmentation capacitors. Two tuning–matching PCB, for respectively 0 and 90^∘ driving, are inserted on the lower part of the coil.

4.2.3 A comparison: SHS4 coil versus birdcage

Images have been acquired using the 3 T MRI from RS²D company using a spin echo sequence. The sample consisted in a cylindrical tube (26 mm diameter – 38 mm length) filled of water + CuS0₄ (allowing a decrease in the longitudinal relaxation time). The images obtained using a 12-leg quadrature birdcage coil on one hand and quadrature SHS4 coil on the other hand are reported in Fig. 5. Probes were fed through a 0–90^∘ hybrid coupler device. For testing in single-channel mode the hybrid coupler was used through the 0^∘ channel, while a 50Ω was put at the output of the 0^∘ channel.

Figure 5 (a) is the one obtained using the quadrature birdcage while (b) has been obtained using the quadrature SHS4 coil. The imaging sequence is a MRI spin echo sequence with following parameters: T_E=10 ms (echo time), T_R=600 ms (repetition time), field of view $=\mathrm{50}\mathrm{mm}\times \mathrm{50}\mathrm{mm}$, slice thickness =1 mm, average =1 and resolution $=\mathrm{256}\times \mathrm{256}$).

Next, the SNR measurements between different ¹H 3 T coils (i.e., birdcage coil, saddle coil and SHS4 coil, single channel or quadrature-driven) are summarized in Table 2.

Table 2 SNR comparisons between birdcage coil, saddle coil and SHS4 measured on the same sample, with identical pulse sequence parameters, in a 3 T MRI from RS²D; n/a denotes not applicable.

5 Discussion

The experimental SNR comparison of SHS prototypes at low and high magnetic field with respect to both saddle coil and birdcage coil validated the modeled SNR increase. This SNR increase was also confirmed between SHS4 and birdcage using quadrature-driven coil (∼35 %). However, it is noticeable that the single- and quadrature-channel mode exhibit a SNR difference higher than the classical 3 dB. We hypothesize this difference is attributable to this non-optimal configuration. The homogeneity of quadrature SHS4 coil proven by image acquiring is roughly comparable to the one of birdcage (also in quadrature), making the saddle-like SHS coil a relevant MRI probe competitor. However, the superiority of SHS coil could be limited for higher-volume samples in which the noise will become dominated by magnetic and dielectric noise. From Eq. (11) we can roughly express the SNR dependency as $\propto \frac{{\mathrm{\Sigma }}_{n=\mathrm{1}}^N\cos \left({\mathit{\theta }}_n\right)}{\sqrt{N}}$; thus, for instance using four pairs of coils, the SNR of the SHS coil would increase by approximately a factor of 2. However, the increased of number of pairs of coils could be limited by complexity and especially at high frequency where the occurrence of the proximity effect becomes preponderant.

6 Conclusions

The SHS method allows one to easily determine the position of electrical conductor favoring the production of a homogenous magnetic field. The method was previously tested in the context of spherical coil for static magnetic field. The present work concerned the design of NMR or MRI probes based on this method. Saddle-like SHS coils have been constructed for different frequency regimes (from 336 kHz up to 128 MHz) in the context of ¹H NMR and MRI. The saddle-like SHS coil has been proved to be driven in quadrature. The experimental comparisons between saddle-like SHS coil, saddle coil and commercial birdcage of comparable sizes validate the higher performances in terms of both homogeneity and SNR of the SHS coils. The higher performance obtained makes the SHS probe valuable for NMR and MRI experiment. Additionally, the great simplicity of design of SHS coils, with respect to the complexity of the birdcage, should be highlighted.

Appendix A: Detailed calculation of Bwire_n and Barc_n

We consider first a single wire “1” of height L parallel to z and centered in the x–y plane whose middle is located at a distance R from the orthonormal, forming an angle θ with x axis, while α corresponds to the angle between the position vector (r) and the x–y plane. The magnetic field generated by this “1” wire at the center of the SHS coil is expressed using Biot–Savart law:

$$\begin{array}{}\text{(A1)}& \mathrm{d}\mathit{B}={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}I}{\mathrm{4}\mathit{\pi }}}{\displaystyle \frac{\mathrm{d}\mathit{l}\wedge \mathit{r}}{\parallel \mathit{r}{\parallel }^{\mathrm{3}}}},\end{array}$$

where $\mathrm{d}\mathit{l}=[\mathrm{0};\mathrm{0};\mathrm{d}z]$, $\mathit{r}=\left[R\cos \right(\mathit{\theta });-R\sin (\mathit{\theta });z]$, z=Rtan α and $\parallel \mathit{r}\parallel =\sqrt{R^{\mathrm{2}}+z^{\mathrm{2}}}$, which becomes $\parallel \mathit{r}\parallel =R/\cos \left(\mathit{\alpha }\right)$. Thus dz is expressed $R/{\cos }^{\mathrm{2}}\mathit{\alpha }\times \mathrm{d}\mathit{\alpha }$. It results that dB has only components in the x–y plane:

$$\mathrm{d}\mathit{B}={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}I}{\mathrm{4}\mathit{\pi }\parallel \mathit{r}{\parallel }^{\mathrm{3}}}}\left[\begin{array}{c}Rdz\sin \left(\mathit{\theta }\right)\\ Rdz\cos \left(\mathit{\theta }\right)\\ \mathrm{0}\end{array}\right].$$

Then,

$$\mathrm{d}\mathit{B}={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}I}{\mathrm{4}\mathit{\pi }R}}\cos \left(\mathit{\alpha }\right)\mathrm{d}\mathit{\alpha }\left[\begin{array}{c}\sin \left(\mathit{\theta }\right)\\ \cos \left(\mathit{\theta }\right)\\ \mathrm{0}\end{array}\right].$$

The integration of dB over the wire length (from $-L/\mathrm{2}$ to $+L/\mathrm{2}$) is expressed

$$\begin{array}{c}{\displaystyle }\mathrm{d}\mathit{B}=\underset{-\arctan (L/(\mathrm{2}R\left)\right)}{\overset{\arctan (L/(\mathrm{2}R\left)\right)}{\int }}{\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}I}{\mathrm{4}\mathit{\pi }R}}\cos \left(\mathit{\alpha }\right)\mathrm{d}\mathit{\alpha }\left[\begin{array}{c}\sin \left(\mathit{\theta }\right)\\ \cos \left(\mathit{\theta }\right)\\ \mathrm{0}\end{array}\right]\\ {\displaystyle }\mathit{B}={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}I}{\mathrm{2}\mathit{\pi }R}}\sin \left(\arctan \right(L/\left(\mathrm{2}R\right)\left)\right)\left[\begin{array}{c}\sin \left(\mathit{\theta }\right)\\ \cos \left(\mathit{\theta }\right)\\ \mathrm{0}\end{array}\right].\end{array}$$

Let us now calculate sin (arctan (u)) where we define θ=arctan (u). First, we start from $\tan \left(\mathit{\theta }\right)=\sin \left(\mathit{\theta }\right)/\cos \left(\mathit{\theta }\right)$, which can be rewritten

$$\begin{array}{}\text{(A2)}& \tan \left(\arctan \right(u\left)\right)={\displaystyle \frac{\sin \left(\arctan \right(u\left)\right)}{\cos \left(\arctan \right(u\left)\right)}},\end{array}$$

which becomes

$$\begin{array}{}\text{(A3)}& \sin \left(\arctan \right(u\left)\right)=u\times \cos \left(\arctan \right(u\left)\right).\end{array}$$

Next, since

$$\begin{array}{}\text{(A4)}& \mathrm{1}+{\tan }^{\mathrm{2}}\left(\mathit{\theta }\right)=\mathrm{1}/{\cos }^{\mathrm{2}}\left(\mathit{\theta }\right),\end{array}$$

we get

$$\begin{array}{}\text{(A5)}& \mathrm{1}+{\tan }^{\mathrm{2}}\left(\arctan \right(u\left)\right)=\mathrm{1}/{\cos }^{\mathrm{2}}\left(\arctan \right(u\left)\right),\end{array}$$

which becomes

$$\begin{array}{}\text{(A6)}& \cos \left(\arctan \right(u\left)\right)={\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{1}+u^{\mathrm{2}}}}}.\end{array}$$

By combining these equations we finally get

$$\begin{array}{}\text{(A7)}& \sin \left(\arctan \right(u\left)\right)={\displaystyle \frac{u}{\sqrt{\mathrm{1}+u^{\mathrm{2}}}}}.\end{array}$$

Thanks to the writing of sin (arctan (u)) we express the magnetic field:

$$\mathit{B}={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}I}{\mathrm{4}\mathit{\pi }R}}{\displaystyle \frac{L}{\sqrt{R^{\mathrm{2}}+(L/\mathrm{2}{)}^{\mathrm{2}}}}}\left[\begin{array}{c}\sin \left(\mathit{\theta }\right)\\ \cos \left(\mathit{\theta }\right)\\ \mathrm{0}\end{array}\right].$$

Lastly, we sum the contribution of the four wires. By writing $B_w=\frac{{\mathit{\mu }}_{\mathrm{0}}I}{\mathrm{4}\mathit{\pi }R}\frac{L}{\sqrt{R^{\mathrm{2}}+(L/\mathrm{2}{)}^{\mathrm{2}}}}$, each magnetic field contribution for wires 1−4 is expressed

$$\begin{array}{}\text{(A8)}& {\displaystyle }{\mathit{B}}_{\mathrm{1}}=B_{\mathrm{w}}\left[\sin \right(\mathit{\theta });\cos (\mathit{\theta });\mathrm{0}]\text{(A9)}& {\displaystyle }{\mathit{B}}_{\mathrm{2}}=B_{\mathrm{w}}[-\sin (\mathit{\theta });\cos (\mathit{\theta });\mathrm{0}]\text{(A10)}& {\displaystyle }{\mathit{B}}_{\mathrm{3}}=B_{\mathrm{w}}[-\sin (\mathit{\theta });\cos (\mathit{\theta });\mathrm{0}]\text{(A11)}& {\displaystyle }{\mathit{B}}_{\mathrm{4}}=B_{\mathrm{w}}\left[\sin \right(\mathit{\theta });\cos (\mathit{\theta });\mathrm{0}].\end{array}$$

Thus the resultant magnetic field of the wires portion for nth coil (Bwire_n), at an angular position θ_n and flown by a current I_n, will have contribution in y-axis direction which is given by

$$\begin{array}{}\text{(A12)}& {\mathrm{Bwire}}_n={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}{I}_n}{\mathit{\pi }R}}{\displaystyle \frac{L}{\sqrt{R^{\mathrm{2}}+(L/\mathrm{2}{)}^{\mathrm{2}}}}}cos\left({\mathit{\theta }}_n\right).\end{array}$$

Next, the contribution of an arc portion (in the x–y plane, thus z=0) is obtained by writing the elementary circuit portion: $\mathrm{d}\mathit{l}=\left[R\mathrm{d}\mathit{\theta }\cos \right(\mathit{\theta }-\mathit{\pi }/\mathrm{2});R\mathrm{d}\mathit{\theta }\sin (\mathit{\theta }-\mathit{\pi }/\mathrm{2});\mathrm{0}]$ and the distance vector $\mathit{r}=\left[R\cos \right(\mathit{\theta });R\sin (\mathit{\theta });z]$. Since two arc portions are opposite, the opposite elementary circuit portion is $\mathrm{d}{\mathit{l}}^{\mathbf{\prime }}=\left[R\mathrm{d}\mathit{\theta }\cos \right(\mathit{\pi }/\mathrm{2}-\mathit{\theta });R\mathrm{d}\mathit{\theta }\sin (\mathit{\pi }/\mathrm{2}-\mathit{\theta });\mathrm{0}]$. The resulting contribution of d$\mathit{l}+\mathrm{d}{\mathit{l}}^{\mathbf{\prime }}$ produces a magnetic field contribution (dB_arc1) given by

$$\mathrm{d}{\mathit{B}}_{\mathrm{arc}\mathrm{1}}={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}I}{(R^{\mathrm{2}}+z^{\mathrm{2}}{)}^{\mathrm{3}/\mathrm{2})}}}\left[\begin{array}{c}-\mathrm{2}Rz\mathrm{d}\mathit{\theta }\cos (\mathit{\theta }-\mathit{\pi }/\mathrm{2})\\ \mathrm{2}{R}^{\mathrm{2}}\mathrm{d}\mathit{\theta }\sin \left(\mathit{\theta }\right)\cos (\mathit{\theta }-\mathit{\pi }/\mathrm{2})\\ \mathrm{0}\end{array}\right].$$

Then, the same contribution produced by the two opposite arc but shifted at $z=L/\mathrm{2}$ becomes

$$\mathrm{d}{\mathit{B}}_{\mathrm{arc}\mathrm{1}}={\mathit{\alpha }}_{\mathrm{1}}\left[\begin{array}{c}-\mathrm{2}R(z-L/\mathrm{2})\mathrm{d}\mathit{\theta }\cos (\mathit{\theta }-\mathit{\pi }/\mathrm{2})\\ \mathrm{2}{R}^{\mathrm{2}}\mathrm{d}\mathit{\theta }\sin \left(\mathit{\theta }\right)\cos (\mathit{\theta }-\mathit{\pi }/\mathrm{2})\\ \mathrm{0}\\ ,\end{array}\right]$$

where ${\mathit{\alpha }}_{\mathrm{1}}=\frac{{\mathit{\mu }}_{\mathrm{0}}I}{(R^{\mathrm{2}}+(z-L/\mathrm{2}{)}^{\mathrm{2}}{)}^{\mathrm{3}/\mathrm{2})}}$. Similarly, the contribution of the two arcs at position $z=-L/\mathrm{2}$ and flown by current −I is written as

$$\mathrm{d}{\mathit{B}}_{\mathrm{arc}\mathrm{2}}={\mathit{\alpha }}_{\mathrm{2}}\left[\begin{array}{c}-\mathrm{2}R(z+L/\mathrm{2})\mathrm{d}\mathit{\theta }\cos (\mathit{\theta }-\mathit{\pi }/\mathrm{2})\\ \mathrm{2}{R}^{\mathrm{2}}\mathrm{d}\mathit{\theta }\sin \left(\mathit{\theta }\right)\cos (\mathit{\theta }-\mathit{\pi }/\mathrm{2})\\ \mathrm{0}\end{array}\right],$$

where ${\mathit{\alpha }}_{\mathrm{2}}=-\frac{{\mathit{\mu }}_{\mathrm{0}}I}{(R^{\mathrm{2}}+(z+L/\mathrm{2}{)}^{\mathrm{2}}{)}^{\mathrm{3}/\mathrm{2})}}$. The combination of dB_arc2 and dB_arc2 at the center of the coil (z=0) is written as

$$\mathrm{d}{\mathit{B}}_{\mathrm{arc}}={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{0}}I}{(R^{\mathrm{2}}+(L/\mathrm{2}{)}^{\mathrm{2}}{)}^{\mathrm{3}/\mathrm{2})}}}\left[\begin{array}{c}\mathrm{2}RL\mathrm{d}\mathit{\theta }\cos (\mathit{\theta }-\mathit{\pi }/\mathrm{2})\\ \mathrm{0}\\ \mathrm{0}\end{array}\right].$$

Lastly, the integration of dB_arc over θ will be

$$\begin{array}{}\text{(A13)}& {\mathrm{dBarc}}_n={\displaystyle \frac{\mathrm{2}{\mathit{\mu }}_{\mathrm{0}}RL{I}_n}{(R^{\mathrm{2}}+(L/\mathrm{2}{)}^{\mathrm{2}}{)}^{\mathrm{3}/\mathrm{2}}}}\cos \left({\mathit{\theta }}_n\right).\end{array}$$

By integration over θ_n, the total contribution on y axis of the arc portion at the center of the coil (Barc_n) is given by

$$\begin{array}{}\text{(A14)}& {\mathrm{Barc}}_n={\displaystyle \frac{\mathrm{2}{\mathit{\mu }}_{\mathrm{0}}RL{I}_n}{(R^{\mathrm{2}}+(L/\mathrm{2}{)}^{\mathrm{2}}{)}^{\mathrm{3}/\mathrm{2}}}}\cos \left({\mathit{\theta }}_n\right).\end{array}$$