A classification technique of civil objects by artificial neural networks using estimation of entropy on synthetic aperture radar images

The article discusses the method for the classification of non-moving civil objects for information received from unmanned aerial vehicles (UAVs) by synthetic aperture radar (SAR). A theoretical approach to analysis of civil objects can be estimated by cross-entropy using a naive Bayesian classifier. The entropy of target spots on SAR images revaluates depending on the altitude and aspect angle of a UAV. The paper shows that classification of the target for three classes able to predict with fair accuracy $P=\mathrm{0},\mathrm{964}$ based on an artificial neural network. The study of results reveals an advantage compared with other radar recognition methods for a criterion of the constant false-alarm rate (P_CFAR<0.01). The reliability was confirmed by checking the initial data using principal component analysis.

1 Introduction

The trend of the modern airborne radar systems for ground monitoring is the introduction of machine learning and artificial intelligence technologies (Gini, 2008). The methods using automatic detection and recognition of the objects over the underlying surface are required in the tasks of terrain mapping, aerial photography, and video fixation (Pillai et al., 2008; Soumekh, 1999). The physical principles of radar recognition are based on the received echo signals from radar contrast targets, Doppler shifts of moving objects, and changes in the polarization structure of the reflected wave (Lee and Pottier, 2009).

One of the prospective directions is the use of unmanned aerial vehicles (UAVs), which monitor the Earth's surface by synthetic aperture radar (SAR). These radar systems ensure images in real time are received at different altitudes and varying aspect angles (Moreira et al., 2013; Long et al., 2019).

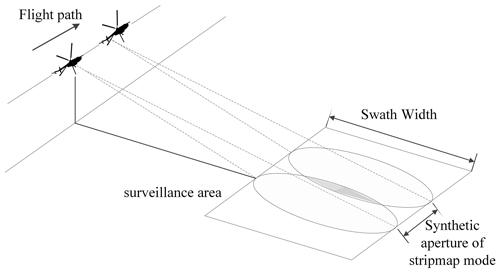
The modern development of SAR includes the use of the so-called homogeneous environment and applications for MIMO systems (Moreira et al., 2013). An important characteristic of the automatic target recognition (ATR) is a constant false-alarm rate (CFAR) (Zhoufeng et al., 2002; Jung et al., 2009), the type of radar polarization (Lee and Pottier, 2009), and SAR imaging modes (stripmap or spotlight mode). The potential accuracy can reach 0.3 m with a linear resolution using multilook processing in the spaceborne radar (Kim et al., 2014; Novak et al., 1998) (Fig. 1).

The UAV application of the SAR mode does not allow such a resolution to be achieved and, therefore, detecting objects in the region of interest (ROI) is usually difficult.

It is advisable to use spatial characteristics for the group of targets detected by UAV within the conditions of an accessible radar map (Novak et al., 1998). Such research was treated in an article (Kvasnov, 2019) where spatial features from the Terra-SAT satellite were used to detect an area with a set of the objects. A further development can be carried out as a recognition of the ground groups in a given area. Such a group can be infrastructure elements in civilian applications (town blocks, agricultural field, sea docks, etc.) (Yin et al., 2007; Moulton et al., 2008). Any vehicles (cars in parking, planes on the airstrip) can have an order of location (Halversen et al., 1994; Owirka et al., 1995). At the same time, the ROI must have a reference point in the course of UAV monitoring the terrain as a condition for civil object recognition (Labowski et al., 2016). The reference point is to be a previously identified object (for example, a road, forest, or building) (Fig. 2) (Huimin and Baoshu, 2007).

Figure 1 Synthetic aperture radar (SAR) of stripmap mode in UAV.

Figure 2 Region of interest (ROI) on the map in SAR.

According to the concept of high-level classification (El-Darymli et al., 2016), we will consider the feature-based approach that can be implemented as a single multi-class classifier. There is a set of the mathematical models for ATR SAR:

• Bayes classifier (Kvasnov, 2020);

• linear discriminant function (Srinivas et al., 2014; Yu et al., 2011);

• neural networks (Cho and Park, 2018; Ernisse et al., 1997).

The analysis of the civil targets can be implemented on based situational modelling with templates (Huimin and Baoshu, 2007). Therefore, in order to get a template of the dataset, we will use artificial neural networks based on a multilayer perceptron (El-Darymli et al., 2016; Ernisse et al., 1997). Most of these papers do not take into account the speckle of the image, which can vary depending on UAV altitude (Ullmann et al., 2018).

The purpose of the article is to consider the ATC method for the non-moving civil objects by spatial characteristics in SAR mode. We suppose the technique focuses on analysis of ROI where essential fluctuations of entropy exist after estimating entire features of image artificial neural network constructs in order to recognize the object group. The training data have been used for different resolution. Examples of SAR images (Figs. 2, 3, and 4) are demonstrated from the resource https://www.sandia.gov (last access: 5 July 2021).

2 Theoretical approach to tasks of radar recognition

Let us have a finite number of the group objects (classes) $Y_n:n\in N$ that must be classified. A set of the observations (features) is given, $X_m:m\in N$, which corresponded to known classes. There is an unknown transformation of the set X_m→Y_n on a finite volume of the training sample $F\mathit{\left\{}\right(x_{\mathrm{1}},y_{\mathrm{1}}),\mathrm{\dots },(x_m,y_n\left)\mathit{\right\}}$. It is required to construct such an algorithm for the initial data F that provided the minimization of the loss function at the output (Wang et al., 2015):

$$\begin{array}{}\text{(1)}& \left\{X_m\to Y_n\right\}:\mathrm{CE}\left(Y_n\right)\to \min .\end{array}$$

The object classification algorithm will be constructed by using the gradient descent method. Then we define the cross-entropy as a loss function:

$$\begin{array}{}\text{(2)}& \mathrm{CE}\left(Y\right)=H\left(p\right)+D_{\mathrm{KL}}\left(p∥q\right),\end{array}$$

where H(p) and D_KL(p∥q) are entropy and relative entropy (Kullback–Leibler divergence) over probability distributions p(y) and q(y), respectively; p(y) is the classification model of the binary indicator; q(y) is the predicted model of probability.

We will consider a training sample where the labels of recognition objects are fixed: Y_nconst; then, H(p)=const. After rewriting, Eq. (3) as a logistic function is

$$\begin{array}{}\text{(3)}& \begin{array}{rl}\mathrm{CE}\left(Y\right)& =D_{\mathrm{KL}}\left(p∥q\right)=-\sum _{i=\mathrm{1}}^n\left[\left(p_i\right)\log \left(q_i\right)\right.\\ & \left.+\left(\mathrm{1}-p_i\right)\log \left(\mathrm{1}-q_i\right)\right].\end{array}\end{array}$$

The function CE(Y) tends to fit the forecasting distribution to the asymptotic value, penalizing both erroneous predictions (1−p_i) and uncertain predictions (p_i<1). We will use CE(Y) as a measure between the real target and noise for SAR images.

In order to estimate the efficiency of the concluded results of classification, we will use principal component analysis (Karhunen–Loève theorem). This method is defined to assess the independence of features and determine the most critical of them. Mathematical implementation is the estimation of the covariance matrix with the minimum number of elements on the main diagonal. The empirical covariance matrix can be obtained from the training sample $F\mathit{\left\{}\right(x_{\mathrm{1}},y_{\mathrm{1}}),\mathrm{\dots },(x_m,y_n\left)\mathit{\right\}}$:

$$\begin{array}{}\text{(4)}& {\mathbf{C}}_{m\times m}={\displaystyle \frac{\mathrm{1}}{n}}{X}^{T}X\forall n>m.\end{array}$$

The estimation of the principal components is carried out on centred data 〈x_m〉, so that $\langle x_m\rangle =x_m-\stackrel{\mathrm{‾}}{x}$. The covariance matrix C_m×m is able to be represented in the canonical form (spectral matrix decomposition) of eigenvalues (Λ) and eigenvectors (V):

$$\begin{array}{}\text{(5)}& {\mathbf{C}}_{m\times m}=\mathbf{V}\mathrm{\Lambda }{\mathbf{V}}^{-\mathrm{1}},\end{array}$$

where V is a matrix whose columns are eigenvectors of the matrix C_m×m; $\mathrm{\Lambda }=\mathrm{diag}\left(\begin{array}{lll}{\mathit{\lambda }}_{\mathrm{1}}& \mathrm{\dots }& {\mathit{\lambda }}_m\end{array}\right)$ is a diagonal matrix with corresponding eigenvalues on the main diagonal; V⁻¹ is the inverse matrix to matrix V.

There are problems of seeking orthogonal projections with the maximum scattering. Then principal component vectors are an orthonormal set $\mathbf{V}={\left[\begin{array}{lll}{v}_{\mathrm{1}}& \mathrm{\dots }& v_m\end{array}\right]}^T$, which comprises eigenvectors of the covariance matrix C, allocated in decreasing order of eigenvalues $\mathit{\lambda }:{\mathit{\lambda }}_{\mathrm{1}}\ge {\mathit{\lambda }}_{\mathrm{2}}\ge \mathrm{\dots }\ge {\mathit{\lambda }}_m$. In order to estimate the number of principal components, we use the relative squared error ${\mathit{\delta }}_k^{\mathrm{2}}$ for the first k components:

$$\begin{array}{}\text{(6)}& {\mathit{\delta }}_k^{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{\mathbf{tr}\left(\mathbf{C}\right)}}\left[\mathbf{tr}\left(\mathbf{C}\right)-\sum _{i=\mathrm{1}}^k{\mathit{\lambda }}_i\right],\end{array}$$

where tr(C) is the covariance matrix trace C.

After projection onto the first k principal components, it is convenient to normalize the covariance matrix by unit variance. Hence, for each coordinate this value is $q_i/\sqrt{{\mathit{\lambda }}_i}$.

3 Mathematical model of recognition on SAR images

The exposal of UAV can essentially vary quality characteristics of studied SAR images. When we focus on ROI, the speckle pattern of this picture has a unique degree of entropy. According to the given condition, Eq. (2), cross-entropy of the target spot under study is able to fluctuate. We need to create a method which allows us to find the best option for extracting an informative parameter from images.

3.1 Mathematical decision

According to Eq. (1), our object is to find an estimate of the conditional probability p(Y|x_i). If we make an assumption about the independence of the features x_i∈X_m, then the solution can be found as a product of the naive Bayesian classifier:

$$\begin{array}{}\text{(7)}& p\left(\left.Y\right|x_i\right)=p\left(Y\right)\times \prod _{i}p\left(\left.x_i\right|Y\right),\end{array}$$

where p(Y) is the average probability of all recognition classes y_j∈Y_n; p(x_i|Y) is the likelihood function for an arbitrary feature x_i, conditional on the set of classes Y being known.

If new data CE(Y|x_i) enter instead of initial data, CE(Y), they would add the expected amount of uncertainty in Eq. (3):

$$\begin{array}{}\text{(8)}& \mathrm{CE}\left(\left.Y\right|x_i\right)=\sum _{y}p\left(Y,x_i\right)\log {\displaystyle \frac{p\left(Y,x_i\right)}{p\left(Y\right)}}.\end{array}$$

We considered the case p_i=1; then, in Eq. (3) there will remain one additive component. When we substitute Eq. (7) into Eq. (8) and simplify the equation, we will get

$$\begin{array}{}\text{(9)}& \mathrm{CE}\left(\left.Y\right|x_i\right)=-\sum _i\left(p\left(y_i\right)\log \left[q\left(\left.\right|y_i\right)\right]+H_Y\left(\mathrm{\Im }\right)\right),\end{array}$$

where $H_Y\left(\mathrm{\Im }\right)=p\left(y_i\right)\sum _j\log \left[q\right(\left.x_j\right|y_i\left)\right]$ is conditional entropy introduced by a feature x_j provided that class y_i∈Y is known.

The maximization CE(Y|x_i) in Eq. (9) is defined by the influence of conditional entropy. Obviously, the extreme value in Eq. (9) can be calculated as a maximum likelihood estimation that is not a trivial task (Gini, 2008). On the other hand, it is appropriate to focus on choosing meanings x_j according to experimental data.

3.2 Task application

In our study, we tried to find a set of the features for the classification procedure (Table 1). These features took into account the regularity of their occurrence for the object under consideration. For example, a stretch of miscellaneous random spots has an association with the extended target. At the same time, vehicles in parking are order elements of similar spots on the SAR image.

Table 1 Chosen features for classification.

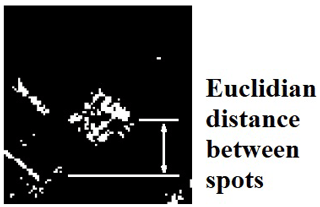
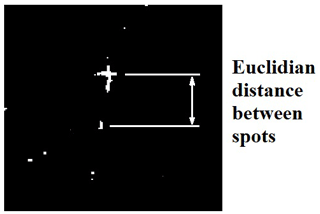
The obtained SAR images are usually presented as grey-scale pictures (Soumekh, 1999). Morphological processing makes it possible to evaluate differences between target spots and noise using the value of entropy. Hence, the binarized image allows detection of point objects by the brightness threshold and further collecting them in an extended target (Wang et al., 2015) (Figs. 3–8).

Figure 3 Extended target on the SAR image (block of town).

Figure 4 Point targets on the SAR image (power lines).

Figure 5 Binarized extended target.

Figure 6 Binarized point targets.

Figure 7 Scheme of the civil object (extended object).

Figure 8 Scheme of the civil object (point objects).

Entropy meanings are different if the speckle pattern of images is analysed. If the SAR image comes closer to the underlying terrain, then entropy is slightly higher: H₁>H₂. At the same time cross-entropy changes are more essential than speckle pattern CE₁>CE₂ (Figs. 3 and 4). Optimal result CE can be found according to Eq. (9) as a function-binarized threshold and selection of SAR images for different altitudes and aspect angles (Figs. 5 and 6) (Knott et al., 2004).

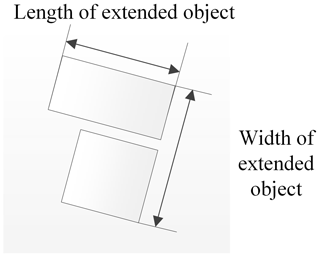
Initially, the spatial characteristics of civil objects are derived from entire target spots that are extracted from a binarized image. Then all objects are identified by the cluster analysis method (Figs. 7 and 8). We should separate objects that are used as extended targets (ETs) and single group targets (SGTs) (Zhu et al., 2004). In order to apply the condition, we use Eq. (10):

$$\begin{array}{}\text{(10)}& \forall \mathrm{\Omega }={\left\{x_i,y_i\right\}}_{i=\mathrm{1}}^k\Rightarrow \left\{\begin{array}{lcl}\mathrm{ET},& \mathrm{if}& \mathrm{dist}\left(x_i,y_i\right)<T,\\ \mathrm{SGT},& \mathrm{if}& \mathrm{dist}\left(x_i,y_i\right)\ge T,\end{array}\right.\end{array}$$

where Ω is the finite domain of the coordinate for spots in ROI; x_i and y_i are Cartesian coordinates of binarized target spots in ROI; dist(x_i,y_i) is the pairwise averaged Euclidean distance between all objects on the plane; T is the distance threshold between all binarized target spots in ROI.

It is important to emphasize that the number and size of binarized spots depend on the altitude and aspect angle of a UAV. For example, the correlation coefficient between features extracted from perfect aspect angle estimated data and from 10^∘ aspect angle error data is 0.983 (Doo et al., 2017). Based on the last statement, we choose the distance threshold according to experimental data assuming the radar accuracy does not exceed 1 m per pixel (Soumekh, 1999).

4 Construct a neural network for civil objects

The initial information of targets was obtained as an extraction of the miscellaneous spots on the binarized SAR image. The civil objects were chosen infrastructure elements (power lines and blocks of town or countryside) and vehicles (cars in parking or agricultural machinery). The number of units (classes) was $Y_n:n=\mathrm{3}$. The total number of features was $X_m:m=\mathrm{4}$. The training data were composed of collections $F\mathit{\left\{}\right(x_{\mathrm{1}},y_{\mathrm{1}}),\mathrm{\dots },(x_{\mathrm{192}},y_{\mathrm{4}}\left)\mathit{\right\}}$.

According to Eq. (3), the cross-entropy value can be simplified if we assume that the shift of the postulated distribution is bias[p(y₀)]→1. Then the competing distributions $q\left(y_{\mathrm{1}}\right)=\mathrm{\dots }=q\left(y_n\right)$ have the distribution density

$$\begin{array}{}\text{(11)}& \begin{array}{rl}\mathrm{CE}\left(Y\right)& =-{\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^n\left[\log \left(p_{\mathrm{0}}\right)+\log \left(\mathrm{1}-p_i\right)\right]\\ & \approx -{\displaystyle \frac{\mathrm{1}}{n}}\log \left[p_o{\left(\mathrm{1}-p_i\right)}^n\right].\end{array}\end{array}$$

An artificial neural network was constructed by gradient descent with adaptive learning rate backpropagation. We used four hidden layers with a log-sigmoid transfer function and a linear output layer. The results of the network are shown in Figs. 9 and 10.

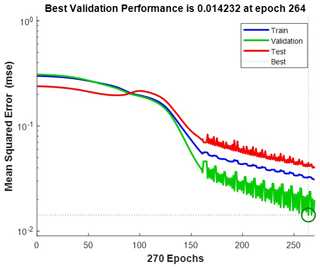
Figure 9 Mean squared error plot as of loss function: training – 70 %, validation – 15 %, test – 15 %.

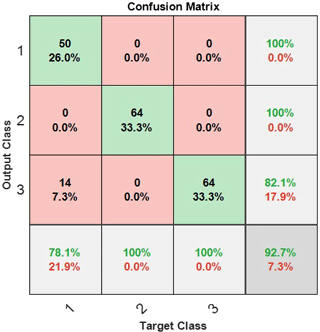
Figure 10 Confusion matrix for recognition classes: 1 – power lines, 2 – block of countryside, 3 – group of vehicles.

It is seen that we have a loss function equal to MSE≈0.014 (Fig. 9), which is quite an appropriate result. There is a probability of class confusion (Fig. 10) when power lines can be detected as a group of vehicles, which then is 〈P_conf〉≈0.07. The other results do not make questions of recognition accuracy.

5 Comparison with other methods

ATC SAR of the non-moving civil objects is illuminated in several articles. In the paper by Kim et al. (2014), the correct classification performance for the final 10- and 20-target classifiers was 77.4 % and 66.2 %, respectively (resolution 1 m per pixel). This result is demonstrably worse than the accuracy of 92.7 % that we got.

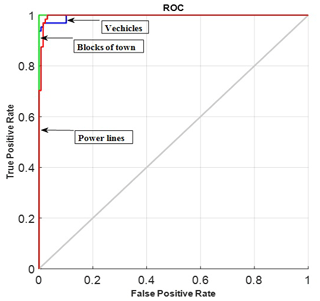
In the paper by Halversen et al. (1994), research was carried out on the recognition of group objects based on automated target cueing. Twenty-four target groups were contained within the dataset; each target group consists of 6 to 11 targets. This research applied only a pure binarized portrait without studying the SAR images that we have made. CFAR reached P_CFAR≈0.29 by high resolution 1 m per pixel. We tried to analyse our data as to the false positive errors using the receiver-operating characteristic (Fig. 11).

Figure 11 Receiver-operating characteristic of three recognition classes.

It appears to be certain that CFAR estimation is lower than in the paper by Halversen et al. (1994) – P_CFAR≤0.01. Thus, our results show a reasonable degree of reliability in recognition of the group objects using a neural network.

The approach to the recognition of the point targets is illustrated in Cho and Park (2018) and Ernisse et al. (1997). Our result (92.7 %) exceeds the value $P\approx \mathrm{0},\mathrm{87}$, which was achieved by using airborne radar by F-15E (Ernisse et al., 1997). The recognition accuracy of 95 % was obtained for the multiple feature-based convolutional neural network method (Cho and Park, 2018). Our result is proportional to this value, but estimation of a false positive rate is omitted that puts in doubt the efficiency of the proposed method.

6 Discussion and estimation of the results

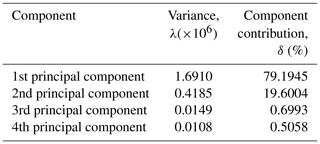
The efficiency of the object classification is proportional to the number of the features and dataset for entire classes $F\mathit{\left\{}\right(x_{\mathrm{1}},y_{\mathrm{1}}),\mathrm{\dots },(x_{\mathrm{4}},y_{\mathrm{192}}\left)\mathit{\right\}}$. We tried to estimate the final result by means of the principal component analysis for the initial dataset (Kawalec et al., 2006). The original reduced training sample $X_m\mathit{\{}{x}_{\mathrm{1}},x_{\mathrm{2}},\mathrm{\dots },x_m\mathit{\}}$ is transformed into an orthogonal basis $V_m\mathit{\{}{v}_{\mathrm{1}},v_{\mathrm{2}},\mathrm{\dots },v_m\mathit{\}}$ according to Eq. (12), where the coordinate axes coincide with the maximum variance in descending order λ_max … λ_min. Each orthogonal component has the contribution on its own that is given in Table 2.

Table 2 Four principal components.

The contribution of the first two main components (out of four evaluated) is δ₅>98 %. The data effectiveness can be estimated based on their projections on the three main axes (Fig. 12).

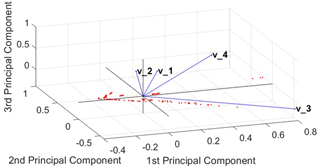
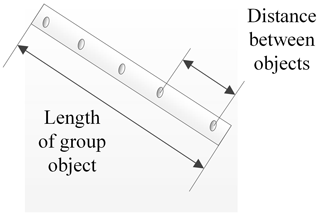
Figure 12 First, second, and third principal components of the training sample: v1 – quantity of objects; v2 – average distance between objects; v3 – length of civil object; v4 – width of civil object.

Having constructed the plot, correlation is demonstrated in the orthogonal basis of the principal components. The graph shows that there is an essential independence between all the original data $V=[\begin{array}{ccc}{v}_{\mathrm{1}}& \mathrm{\dots }& v_{\mathrm{4}}\end{array}{]}^T$. The most dependent features are the length (v₃) and width (v₄) of the group object, respectively. Obviously, any size of spatial object is correlated between each other. Generally, there is no need to extend the space of input classes. Nevertheless, ROI requires choosing a reference point in order for all recognition groups to have disjoint zones on the terrain.

7 Conclusion

The article proposes a classification technique of the non-moving civil objects based on the estimation of entropy that was extracted from SAR images. The studied pictures received UAV at the different altitudes and aspect angles. The choice of recognition features was determined by minimizing the cross-entropy calculated for the model of the naive Bayesian classifier. It is shown that a binarized image can have a different degree of cross-entropy for the target spot with respect to the speckle pattern of images. An efficient classification approach using an artificial neural network was demonstrated.

A training set (192 observations; four features) was used for learning three classes of the non-moving civil targets – power lines, block of town, and group of vehicles. The probability of the object classification is P≈0.927 with a low degree of constant false-alarm rate P_CFAR≤0.01. These indicators are equal to or exceed the other results for the similar methods.

In order to confirm the results of the classification, they were verified by using the principal component analysis. The checking showed an essential degree of decorrelation of studied features. Further research should aim to clarify the spatial characteristics by extending experimental data.