the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Efficient transient testing procedure using a novel experience replay particle swarm optimizer for THD-based robust design and optimization of self-X sensory electronics in industry 4.0
Qummar Zaman
Senan Alraho
Andreas König
This paper aims to improve the traditional calibration method for reconfigurable self-X (self-calibration, self-healing, self-optimize, etc.) sensor interface readout circuit for industry 4.0. A cost-effective test stimulus is applied to the device under test, and the transient response of the system is analyzed to correlate the circuit's characteristics parameters. Due to complexity in the search and objective space of the smart sensory electronics, a novel experience replay particle swarm optimization (ERPSO) algorithm is being proposed and proved a better-searching capability than some currently well-known PSO algorithms. The newly proposed ERPSO expanded the selection producer of the classical PSO by introducing an experience replay buffer (ERB) intending to reduce the probability of trapping into the local minima. The ERB reflects the archive of previously visited global best particles, while its selection is based upon an adaptive epsilon greedy method in the velocity updating model. The performance of the proposed ERPSO algorithm is verified by using eight different popular benchmarking functions. Furthermore, an extrinsic evaluation of the ERPSO algorithm is also examined on a reconfigurable wide swing indirect current-feedback instrumentation amplifier (CFIA). For the later test, we proposed an efficient optimization procedure by using total harmonic distortion analyses of CFIA output to reduce the total number of measurements and save considerable optimization time and cost. The proposed optimization methodology is roughly 3 times faster than the classical optimization process. The circuit is implemented by using Cadence design tools and CMOS 0.35 µm technology from Austria Microsystems (AMS). The efficiency and robustness are the key features of the proposed methodology toward implementing reliable sensory electronic systems for industry 4.0 applications.
- Article
(2844 KB) - Full-text XML
- BibTeX
- EndNote
Machine learning (ML) and artificial intelligence (AI) are considered the electricity for the twentieth century. The integration of AI and ML with other evolving technologies such as cyber-physical systems, big data analytics, cloud computing, and industrial internet of things I(I)oTs is enabling the most noticeable change in the industrial domain (Diez-Olivan et al., 2019) known as industry 4.0 (Kagermann et al., 2013; Abd and König, 2020). I(I)oTs devices and industry 4.0 introduce more demands on sensors and sensory electronics, primarily regarding measurement data accuracy, versatility, flexibility, long-term reliability, and robustness (Koenig, 2018; Trends, 2014). The performance of sensors and sensory electronics is strongly challenged by static and dynamic variations (Lee et al., 2018b; Lin et al., 2019). Fabrication process imperfections such as lithographic uncertainties, mechanical stress due to packaging, and process parameter deviations are referred to as static variations. However, the environmental variations, thermal drift due to external heating and self-heating, power supply fluctuations, and aging effects are considered a dynamic variation (Alraho et al., 2020). Usually, analog sensory electronics are overdesigned to address the static and dynamic variations that result in larger die area and more power consumption.
On the other hand, ML and AI in smart sensory electronics (SSEs) enable the circuit design with the self-X (self-calibration, self-healing, self-optimize, etc.) properties (Kammara et al., 2018a; Lee et al., 2018a) to tackle the variations. AI enables online calibration methods to calibrate the sensory electronics system even after the chip fabrication (Delaine et al., 2019). Calibration methods are realized by designing an integrated circuit (IC) with controllable tuning knobs and performance measurements setup. With the insertion of tuning knobs, SSEs can calibrate themselves to redeem extreme static and dynamic deviations, which relax the power consumption (Lee et al., 2018b). In contrast, the recalibration of SSE comes with the cost of larger parasitics, a bigger die area, and longer configuration or optimization time. This imposes a significant limitation on the dynamic performance of the system. To resolve this remedy, we introduced the reconfigurability only to the sensitive elements, which have a major impact on the overall system performance.
Similarly, the overhead of the performance measurement setup is also considerably essential for SSE in terms of system complexity and measurement time of different quantities. There are two fundamental classifications of the on-chip measurement setup, depending on the assessment criteria of the target performance characteristics. The first class utilizes a direct performance measurement method to verify performance characteristics (Lee et al., 2018b). This scheme offers more accuracy and precision but raises the design complexity and chip area (Andraud et al., 2016). The second class uses the indirect measurement (IM) method that relies on statistical interference. These IM methods output a simultaneous estimation of multiple system performance parameters from simple test stimuli (Andraud et al., 2016; Variyam et al., 2002; Stratigopoulos and Mir, 2012; Natarajan et al., 2010).
Authors in Variyam et al. (2002) applied an optimized multitone signal with the help of an evolutionary algorithm (EA) to the operational amplifier and examined a transient response for the indirect estimation of characteristics such as input common-mode range, gain, slew rate, and bandwidth. To enhance the prediction accuracy, a substitute test flow centered on the two defect filters approach is proposed in Stratigopoulos and Mir (2012). A similar concept is presented in Natarajan et al. (2010), where an envelope detector is applied to infer the target characteristics of the ICs. Nevertheless, in the application of SSE, this category of IMs needed to be optimized due to finite computational resource constraints.
An alternative cost-effective indirect measurement technique using non-intrusive sensors is illustrated by Andraud et al. (2016), in which the sensor is electrically disconnected from the main circuit. As operating conditions of these sensors are strongly correlated with the characteristics of ICs, the target characteristics of the primary circuit can be easily estimated and measured economically from different characteristics of the non-intrusive sensor. It is difficult to approximate the performance predictor analytically; therefore, an artificial neural network (ANN) is usually used as a regressor to approximate the regression task. Besides, the data generation and collection for the training phase of ANN is quite a challenging task, and its complexity increases exponentially with the complexity of a device under test (DUT).
The primary objective of this research paper is to address the missing link for the assessment or optimization unit. It reviews tuning or calibration knobs insertion challenges and the cost-effective performance evaluation setup for self-X SSE. A reconfigurable wide-swing indirect current-feedback instrumentation amplifier (CFIA) is selected as a test vehicle for the extrinsic evolution of the proposed methodology. CFIA is an essential part of measurement systems and sensory readout electronics, particularly for bridge sensors (Alraho and König, 2019).
1.1 Indirect current-feedback instrumentation amplifier (CFIA)
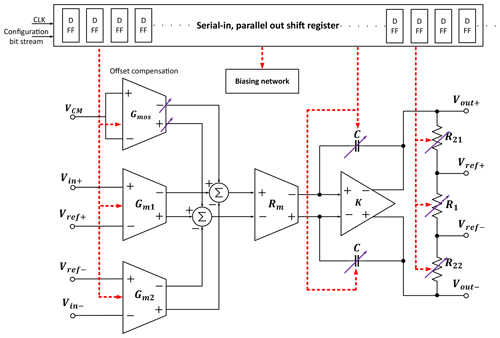
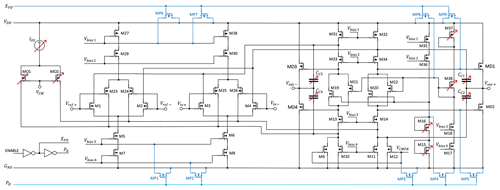
The block diagram of proposed reconfigurable CFIA is shown in Fig. 1, as a continuation of further improvement to our previously proposed work presented in Alraho and König (2019). In-circuit implementation, the major improvement is the considerable reduction in tuning knobs without any scarification of system reconfigurability, which results in the minimization of parasitics and layout area. The proposed system also has an offset calibration block supervised by AI. More details about the circuit can be found in Alraho et al. (2020), while the main focus of this research project is to address the problem of efficient implementation of the calibration method for SSE. A low-cost indirect performance measurement method is being proposed for performance evaluation measurement setup by applying simple test stimuli. It works on the principle of correlation and dependency of different performance characteristics of SSE among one another (Zaman et al., 2020a).
1.2 PSO algorithm
As far as the selection of optimizer for calibration process is concerned, the derivative-based optimizers cannot be applied due to discontinuous objective space. In contrast, meta-heuristic optimization algorithms behave extremely well despite the presence of objective space discontinuity. Therefore, the traditional particle swarm optimization (PSO) (Eberhart and Kennedy, 1995) is utilized after expanding its exploration capabilities as an optimizer to satisfy the requirements of complex search space as well as objective space optimization for SSE. In the last decade, many improved versions of the PSO algorithm have been proposed in the literature to extend its searching capability and minimize the probability of getting trapped into the local minima (Liu et al., 2018; Zhan et al., 2009). As an example, one of the most famous modifications of PSO algorithms is linearly decreasing inertia weight (LDW-PSO) (Shi and Eberhart, 1999). The inertia weight w is defined as follows:
where wmin and wmax represent the minimum and maximum value of the inertia weight w, respectively; “currentIteration” denotes the current running iteration number, and “maxIteration” represents the maximum number of iterations. Usually, a larger value of w achieves the global optimum exploration, and a smaller value performs the local exploitation. Moreover, the PSO algorithm with linearly varying acceleration coefficients (LAC-PSO) has been presented in Ratnaweera et al. (2004). The cognitive scaling factor or acceleration coefficient c1 is linearly decreasing, while the social scaling factor or acceleration coefficient c2 is linearly increasing, which are given as follows:
where c1i,2i and c1f,2f represent the initial and final values of the acceleration coefficients respectively. Liu et al. (2019) recently proposed the sigmoid function (SPSO) based adaptive acceleration coefficients adjustments, which are defined as follows:
where a=0.5, b=1.5, c=0.000035 3.81× search range (distance between upper and lower bound of particle), d=0, and represents the distance of the ith particle to its personal or global best at the kth iteration.
The next class of PSO variants focuses on different updating strategies and new topology structures to enhance the search capabilities. Some well-known topologies are introduced into PSO algorithms include pyramid, clusters, von Neumann, and ring (Tawdross, 2007; Kennedy and Mendes, 2002). In the adaptive PSO algorithm, a new learning strategy has been used to dynamically adjust the parameters based on the evolutionary state (exploitation state, exploration state, convergence state, and jumping-out state) information (Zhan et al., 2009). Furthermore, a switching PSO algorithm is recently proposed in Zeng et al. (2016) to switch between the velocity updating models based on the evolutionary state estimated by a Markov chain model. There are also research activities about the introduction of biological and sociological inspired methods to the PSO, such as the aging theory-based PSO algorithm, the cultural-based PSO algorithm, and the niching PSO algorithm (Zeng et al., 2016; Chen et al., 2012; Brits et al., 2007; Daneshyari and Yen, 2010). However, there is still room for further improvement to enhance the performance of the PSO algorithms, especially for high-dimensional complex multi-objective search space with many local optima (Liu et al., 2018; Zeng et al., 2020; Li et al., 2021), as in the case of SSE optimization.
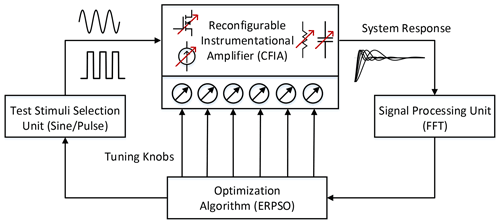
The block diagram of proposed methodology is shown in Fig. 2. As it is mentioned in the literature review, the modified particle swarm optimizer is being used as an optimizing algorithm. The test stimuli selection unit consists of sinusoidal and step signals. The reconfigurable CFIA is being used as a sensory electronics system. Lastly, the signal processing unit performs the total harmonics distortion measurements by performing the fast Fourier transform (FFT) at the CFIA output.
The key idea presented by authors in Variyam et al. (2002) to utilize the EA for generating the effective test stimulus to predict the characteristics of the operational amplifier is being modified here for the SSE environment. It is arduous to generate any arbitrary waveform suggested by EA due to larger computational constraints. The proposed design methodology is established on applying fixed sinusoidal and step signals to solve this issue. It is based on the fact that the characteristics of amplifiers are strongly correlated, e.g., slew rate (SR) and gain-bandwidth product (GBW). The proposed optimization unit first applies the sinusoidal signal to the DUT. By performing the FFT on the system response, most of the design characteristics can be estimated in a single execution, specifically the total harmonics distortion (THD) given as
where f is fundamental frequency and Ai is the complex coefficient from FFT for the ith harmonic and i≠0, f. This is due to the fact that design imperfection like limited GBW, input common-mode range (ICMR), SR, close-loop accuracy, SNR, full-power bandwidth, and the effective number of bits (ENBs) can be translated to nonlinear distortion at the output of the closed-loop amplifier (Johns and Martin, 2008; Ye et al., 2012). The alternative approach to the proposed method is to operate different AC, transient, and DC measurements (Zaman and König, 2019), hence increasing the optimization time and system complexity remarkably. It is beneficial to eliminate the AC test of the amplifier with our proposed methodology since it is not a simple measurement task.
The mixtrinsic evolution first presented in Stoica (1999); Stoica et al. (2000) means a population contains both extrinsic and intrinsic individuals. At the institute of the authors in prior work, Tawdross (2007) extended this concept to perform the complex measurements (open-loop gain, phase margin, and output resistance, etc.) extrinsically on the SPICE simulator and run the simple measurements (common-mode range, output voltage swing, and offset) intrinsically. However, this solution is not appropriate for two reasons. Firstly, simulating circuit modules are not accurate compared to the physical hardware of the DUT. Secondly, it consumes a substantial amount of time restricted by the processing power. Kammara et al. (2018b) developed a circuit synthesizer tool based on transient analysis for nonlinear spiking neuron circuit optimization. However, their proposed method falls under direct measurement methods, while our proposed solution relies on THD measurement to indirectly capture the amplifier non-idealities.
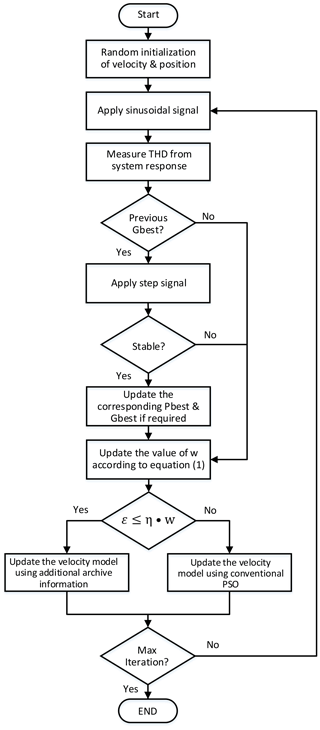
Unfortunately, amplifier stability cannot be predicted from spectrum information obtained by the sinusoidal response. Therefore, the stability of the DUT is analyzed with the help of a system step response. The proposed algorithm performs the step response only if a better fitness value of THD is found compared to the current swarm global best fitness value rather than performing all detailed simulations for every particle. Consequently, it reduces the analog circuits' optimization time drastically. The flow diagram of the proposed design methodology is summarized in Fig. 3. It begins with the random initialization of the velocity and position of the particles. After that, the FFT is performed from the reconfigurable amplifier output signal with the known sinusoidal fundamental frequency. From the resulting output spectrum, the THD value is being calculated using Eq. (4), and this value serves as a fitness or cost function value for the PSO-based optimization. The stability test of the DUT is performed only in the case of a better fitness response obtained. In the next phase, the velocity update equation of the conventional PSO is modified with the help of the previously visited global best minimum. In order to maintain the balance between exploration and exploitation, the epsilon greedy algorithm is utilized, which will be explained in the following up section. This process continues until the end of the maximum number of iterations.
2.1 The proposed experience replay particle swarm optimization (ERPSO)
In this paper we are proposing experience replay particle swarm optimization (ERPSO). The proposed ERPSO expanded the selection producer of the classical PSO by randomly selecting the historic global best of particles with the help of experience replay buffer (ERB) to solve the complex objective space problem of SSE. The novelty of the ERPSO relies upon the introduction of the ERB in the velocity updating equation (VUE) of the conventional PSO algorithm. The ERB concept is usually being employed in the reinforcement learning (Lin, 1992; Schaul et al., 2015) to make use of the accumulated historical values for better convergence accuracy. In the case of ERPSO, the ERB represents the archive of the previously visited global best particles. It helps to minimize the probability of the local minima trapping by taking advantage of prior knowledge instead of using only the most recent experience. The selection of the ERB is performed based on an adaptive epsilon greedy algorithm to maintain the balance between exploration and exploitation (Sutton and Barto, 2018). The basic VUE of ERPSO is given by
where
-
represents the velocity of the ith particle in the jth iteration;
-
w is inertia weight whose value is defined by Eq. (1);
-
are uniformly distributed random numbers [0, 1];
-
c1 and c2 are the cognitive and social coefficients, respectively, and ;
-
and Gt are the personal and global best information of the whole swarm;
-
ε is a random variable whose basic purpose is to introduce epsilon greedy algorithm to balance the exploration and exploitation;
-
η denotes the intensity factor to control the exploration and exploitation;
-
At represents the archive of previously visited global best positions of the swarm.
The position update equation of ERPSO is given as follows:
where represents the position of the ith particle in the jth iteration. According to the proposed VUE, the particles try to quickly converge towards the global optimum with the probability of 1−ε. Therefore, the VUE of the conventional PSO algorithm is used for the first scenario. On the other hand, to minimize the probability of premature convergence, the ERPSO algorithm randomly selects any historic global best solution from the experience reply archive with the probability of ε.
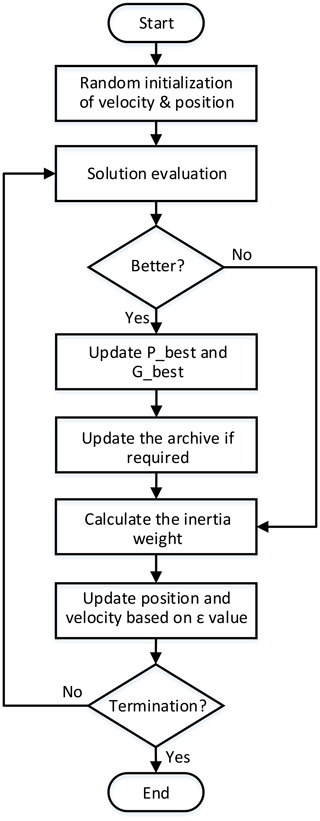
The flow diagram of the ERPSO algorithm is illustrated in Fig. 4. The ERPSO algorithm begins with random initialization of the particles' position and velocity of the particles. Then the fitness value of each particle is evaluated. If the fitness value is better than the particles' global or personal best, the respective field will be updated, and the value of inertial weight w will be calculated based on Eq. (1). In the next step, the velocity of each particle will be updated based on ε value. Finally, the particle's position value will be amended, and this procedure continues until reaching the end of the maximum number of iterations.
2.2 Transistor level design of reconfigurable CFIA
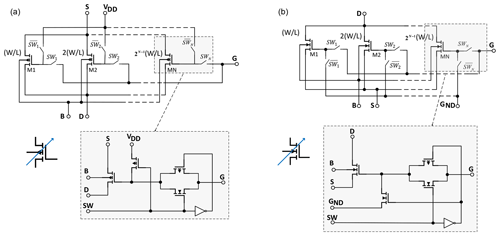
The transistor level design of the proposed fully differential CFIA is presented in Fig. 5 (Alraho et al., 2020; Alraho and König, 2019). The circuit successfully adapted the fully balanced differential-difference amplifier, owing to its important properties of having a wide input voltage span with the possibility of reaching high dynamic performance (Alzaher and Ismail, 2001). The use of complementary input stage plus employing efficient class AB output driver (Hogervorst et al., 1994) allows for maximum signal dynamic range. Based on the presented design approach, the circuit components' first manual cut design values and currents are passed as seed solutions to the optimization unit for further improvement. By inspecting the results obtained during design and optimization iterations, a number of sensitive elements are shortlisted to serve as tuning knobs of the algorithm as listed in Table 1 while keeping other devices fixed to the optimized values. Tuning knobs are programmable arrays incorporating binary-weighted scalable devices controlled by digital patterns generated by the algorithm. Figure 6 depicts scalable NMOS and PMOS transistors, where the gate of the unselected transistors from the array is shorted to the supply voltage for the PMOS or to the ground for the NMOS. This will avoid the saved charge at the floating gate capacitor of the transistor, hence assuring the unselected transistor to be fully off and reducing the leakage current. Similarly, banks of scalable resistors and capacitors are also used in the design.
3.1 Experimental test on benchmarking functions for the ERPSO
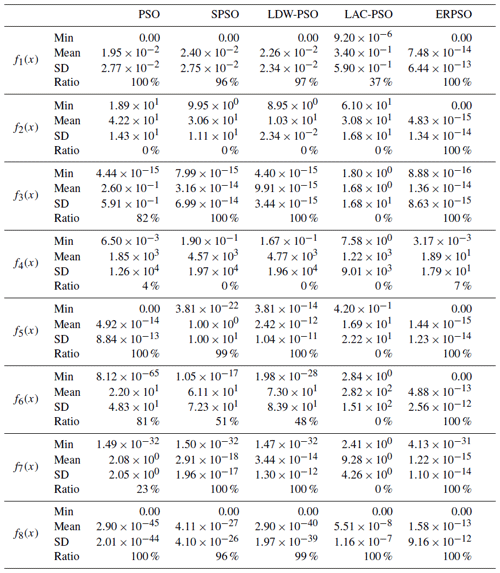
In this work, eight different benchmarking functions (BMFs) are selected from the literature to observe the optimization behavior of the proposed ERPSO. The detailed information about the BMFs is summarized in Table 2. It includes the functions' names, dimensionality, the span of search space, and the global best value. All shortlisted BMFs are high-dimensional problems to approximate the search space complexity of SSE. The Griewank function f1(x) is one of the most popular BMFs that is generally used to verify the convergence rate of optimization algorithms. The Rastrigin function f2(x) and Ackley function f3(x) are hard to optimize due to a large number of local optima. The Rosenbrock function f4(x) (also known as banana or valley function) and the Levy function f7(x) are non-convex functions. The Schwefel 1.2 function f5(x) and Schwefel 2.22 function f6(x) are typical multimodal and unimodal functions, which are difficult to find the global optimum. Lastly, the Sphere unimodal function f8(x) is selected to examine the convergence rate.
This experiment is conducted using 30 particles, 25 dimensions, and 5000 iterations. Each experiment is repeated 100 times to minimize randomness or lucky shots. The performance of the ERPSO algorithm is compared over four famous PSO algorithms, including the LDW-PSO, LAC-PSO, PSO, and SPSO. The convergence curves of the ERPSO algorithms are illustrated in Fig. 7. The horizontal axis represents the number of iterations, and the vertical axis denotes the mean of the fitness value of all the shortlisted PSO algorithms on the logarithmic scale. It can be observed that the convergence rate of the PSO and LAC-PSO is much faster as compared to the ERPSO algorithm. However, the ERPSO algorithm attains a better fitness value of the global minimum compared to other PSO algorithms. The performance of the ERPSO outperforms the other PSO algorithms in all optimization BMFs, which demonstrates the capability of ERPSO to avoid local optimum trapping. In the case of the Ackley and Levy function, the performance of the proposed ERPSO algorithm is comparable to LDW-PSO and outperforms others. Only in the Sphere function does our proposed ERPSO algorithm exhibit less convergence, but it still successfully finds the global optimum. The convergence of the ERPSO can be improved by decreasing the exploration intensity η. However, the exploitation is favored over exploration because of the SSE search space complexity.
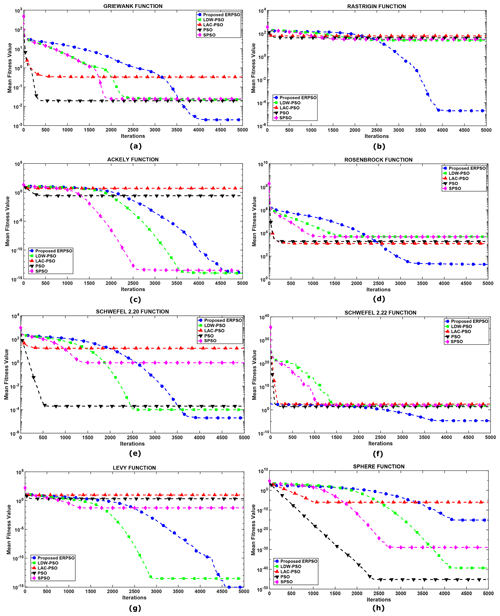
Figure 7Optimization convergence curves for (a) Griewank function f1(x), (b) Rastrigin function f2(x), (c) Ackley function f3(x), (d) Rosenbrock function f4(x), (e) Schwefel 1.2 function f5(x), (f) Schwefel 2.22 function f6(x), (g) Levy function f7(x), and (h) Sphere function f8(x).
Furthermore, the additional information about the optimization process is summarized in Table 3, where the statistical information about the fitness value (minimum, mean, and the standard deviation) of different PSO algorithms for each BMF is presented, including the achieved successful ratio of convergence. The mean value of the ERPSO is lower than the other PSO algorithms, which represents the dominance of the ERPSO in achieving the global minima. As already presented in the discussion of the convergence curves, the convergence rate of the ERPSO is not as rapid as compared to the other PSO algorithms, which has been highlighted here in this table by the mean value of the f8(x). However, the proposed ERPSO algorithm obtained the global minima with the improved mean value for other BMF. Moreover, convergence performance ratio (CPR) is one more essential metric to examine the algorithms' successful attainability of its global optimum. Different variates of the PSO algorithms show very low CPR, like in the Rastrigin function, due to its large local optimums. In contrast, the proposed ERPSO exhibits a much higher CPR value because of the extended exploration capabilities. Only for the Rosenbrock function optimization does the ERPSO give less CPR but still far better than the other algorithms.
3.2 Experimental test on reconfigurable SSE
In the next step, the performance of the ERPSO algorithm is extrinsically evaluated on the complex objective space of the CFIA circuit. For this assessment, a sinusoidal signal with a frequency of 100 kHz and amplitude of 2 Vp-p is applied as a test stimulus for the targeted THD value of −75 dB. For this work, the sine wave signal is generated from the Cadence tools. However, we already started the work on the real implementation of a sinusoidal signal generator by using the direct digital synthesizer (DDS) circuit (Shi and Sánchez-Sinencio, 2015) based on the sine-DAC architecture (Yang and Mason, 2009). The quantized generated signal can be smoothed using anti-imaging (reconstruction low-pass filter) to make the signal closer to the ideal source with a lower THD value. In the next stage, the voltage-controlled voltage source (VCVS) will be used to provide driving capability and to have low output source impedance. Another known technique for generating an on-chip sinusoidal signal is by low-pass filtering the clock signal (Wei et al., 2013). Nevertheless, this approach requires a high-order filter to nullify the harmonic components. Hence the filter circuit consumes a considerable amount of power and chip area. In the step response test, we used pulse signal with a time period of 1 µs and amplitude of 2 Vp-p.
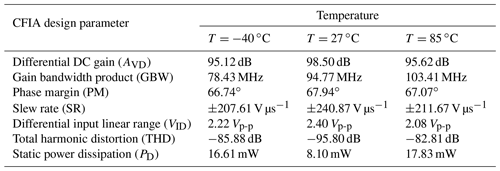
All transistor widths are kept constant to 1 µm for the minimization of channel length modulation effects, and ERPSO only varies the width of sensitive elements as specified in the Table 1. Because this work is intended for the cloud computing applications in industry 4.0 rather than edge computing (Angelopoulos et al., 2020), therefore, we implemented the algorithm and THD extraction from the FFT using Python language, while for the edge computing applications, the implementation of the FFT can be realized by using field-programmable gate array (FPGA) (Saeed et al., 2009) or dedicated on-chip solutions (Chauhan et al., 2013). The CFIA circuit is designed by using Austria Microsystems (ams) with 0.35 µm technology, whereas Cadence virtuoso OCeaN (OCN) is used for the circuit simulation. The achieved performance characteristics of the CFIA after the optimization process are listed in Table 4. The optimization process is performed with RL=100 kΩ, CL=5 pF, industrial temperature range (−40 to +85 ∘C), and unity gain configuration. As it can be observed from Table 4, the proposed designing procedure illustrates the successful optimization of the reconfigurable CFIA by optimizing the THD and pulse response and satisfied most of its characteristics. Also, it can be seen that the ERPSO optimized the circuit performance under temperature variation to model the optimization of dynamic thermal deviation of ICs effectively.
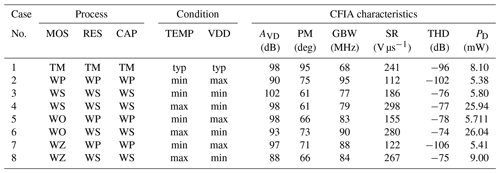
Table 5CFIA performance under worst-case process corners of the AMS 0.35 µm technology. Where VDD(typ) = 3.3 V, VDD(max) = +10 % VDD(typ), VDD(min) = −10 % VDD(typ), ∘C, ∘C, typ: typical, WP: worst-case power, WS: worst-case speed, WO: worst-case one, and WZ: worst-case zero.
The ERPSO algorithm invokes the pulse response only in the case that the global best particle is obtained by the swarm to verify the solution stability. As most of the optimization process performs the sinusoidal response, this results in further reduction of automation time (roughly 3 times less) as compared to our previous work presented in Zaman et al. (2020b); Kammara et al. (2016). In the former work, we followed the classical optimization approach (Vural and Yildirim, 2012), in which an algorithm runs through multiple tests to meet each design specification. The spared time in the newly suggested methodology is especially important for calibrating sensory electronics where tuning time is critical. From the hardware perspective, the potential of our proposed methodology can be further counted due to the relaxation of the measurement setup required for the calibration procedure. Practically, amplifier AC characteristic measurements and data extractions are not a simple task, and they are successfully excluded in our method.
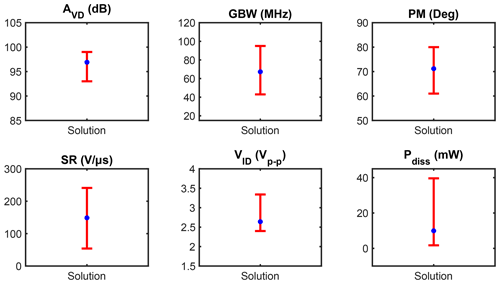
As done with the BMFs, the optimization process is repeated over 10 independent runs, and the statistical optimization information is graphically illustrated using error bar graphs in Fig. 8. In this test, the performance characteristics of the CFIA are extracted from multiple optimization results based on the specified THD value. In order to emulate both the static and dynamic variations' impact on the sensors electronics, the CFIA is subjected to the extreme process, voltage, and temperature (PVT) corners as recommended by AMS foundry and given in Table 5. The ERPSO algorithm upgraded the reconfigurable design for every corner to calibrate for the targeted THD specifications as summarized in Table 5.
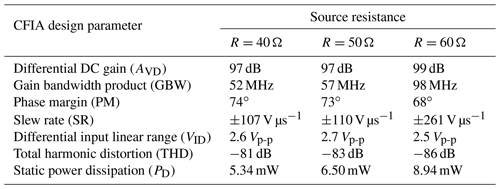
The non-ideality of the measurement assessment unit is nevertheless essential to be considered. It is because the accuracy of the optimized SSE is limited to the precision of this unit. Therefore, a non-ideality of the sinusoidal test signal is being studied by modeling of real sine (voltage) source with an output temperature-dependent resistor. In this experiment, the change of the resistor was 20 % from the nominal value (50 Ω), and the optimization results are summarized in Table 6. It can be concluded that as long as the test sine signal has the THD value above the threshold value, it does not affect the optimization performance.
In this research paper, a novel ERPSO algorithm is presented and successfully deployed to improve the optimization performance of the complex objective space of CFIA. The ERPSO algorithm is increasing the exploration capabilities of the classical PSO algorithm by introducing the ERB. It is worth mentioning that the ERB contained the previously visited global best positions. The preponderance of the proposed ERPSO algorithm is validated over four classical PSO algorithms on eight benchmarking functions. Finally, the proposed ERPSO has been successfully applied for the extrinsic evaluation of the CFIA circuit. For the later experience, a new design approach is introduced based on THD analyses that vary from the traditional calibration approach intended for a particular characteristic of DUT. Instead, the proposed calibration methodology optimizes all characteristics of the reconfigurable SSE at once. Therefore, the DUT can preserve the optimum performance characteristics even in the presence of severe PVT variations and aging effects. The effectiveness of the proposed design methodology is demonstrated by the achieved performance characteristics of the CFIA, hence, offering a flexible and efficient scheme for optimizing reconfigurable sensory electronics systems with self-X properties in industry 4.0 domain. The future work plan can be outlined into four perspectives: (a) performing the intrinsic evaluation that includes the implementation of optimization algorithm and sensor signal processing unit for the FFT and THD measurements, we are going to use the wired sensor platform with Mini PC (R-Pi family), which is an optimal choice for the proof of principle (Picaut et al., 2020); (b) applying the methodology to other sophisticated systems in particular filter optimization and tuning; (c) modeling the dynamic drift of the test stimuli properties and non-idealities of the observer; and (d) integrating low-cost power measurements to supply optimization units with a power constraint.
The underlying coding and data are not publicly available due to a license agreement and data software protection of the Cadence Environment and technology from AMS provided under the umbrella of Europractice.
QZ was responsible for development, implementation, and verification of the algorithm. SA was responsible for the circuit designing and the THD-based idea. AK contributed the concepts of robust observer realization for intrinsic optimization and of optimization with non-ideal assessment unit, suggestion for modification of the PSO architecture, paper structuring, experiment design, paper reviewing and editing, and overall project supervising.
The authors declare that they have no conflict of interest.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the special issue “Sensors and Measurement Science International SMSI 2020”. It is a result of the Sensor and Measurement Science International, Nuremberg, Germany, 22–25 June 2020.
The authors would like to thank the DAAD (Deutscher Akademischer Austauschdienst) for managing the financial support.
This paper was edited by Marco Jose da Silva and reviewed by two anonymous referees.
Abd, H. and König, A.: A Compact Four Transistor CMOS-Design of a Floating Memristor for Adaptive Spiking Neural Networks and Corresponding Self-X Sensor Electronics to Industry 4.0, tm – Technisches Messen, 87, s91–s96, https://doi.org/10.1515/teme-2020-0024, 2020. a
Alraho, S. and König, A.: Wide input range, fully-differential indirect current feedback instrumentation amplifier for self-x sensory systems/Symmetrischer Instrumentierungsverstärker mit indirekter Stromgegenkopplung und hoher Eingangsignalspanne für integrierte Sensorsysteme mit Self-x-Eigenschaften, tm – Technisches Messen, 86, 62–66, https://doi.org/10.1515/teme-2019-0054, 2019. a, b, c
Alraho, S., Zaman, Q., and König, A.: Reconfigurable Wide Input Range, Fully-Differential Indirect Current-Feedback Instrumentation Amplifier with Digital Offset Calibration for Self-X Measurement Systems, tm – Technisches Messen, 87, s85–s90, https://doi.org/10.1515/teme-2020-0021, 2020. a, b, c
Alzaher, H. and Ismail, M.: A CMOS fully balanced differential difference amplifier and its applications, IEEE T. Circ. Syst. II, 48, 614–620, https://doi.org/10.1109/82.943332, 2001. a
Andraud, M., Stratigopoulos, H.-G., and Simeu, E.: One-shot non-intrusive calibration against process variations for analog/RF circuits, IEEE TCAS I, 63, 2022–2035, https://doi.org/10.1109/TCSI.2016.2598184, 2016. a, b, c
Angelopoulos, A., Michailidis, E. T., Nomikos, N., Trakadas, P., Hatziefremidis, A., Voliotis, S., and Zahariadis, T.: Tackling faults in the industry 4.0 era – a survey of machine-learning solutions and key aspects, Sensors, 20, 109, https://doi.org/10.3390/s20010109, 2020. a
Brits, R., Engelbrecht, A. P., and van den Bergh, F.: Locating multiple optima using particle swarm optimization, Appl. Math. Comput., 189, 1859–1883, https://doi.org/10.1016/j.amc.2006.12.066, 2007. a
Chauhan, H., Choi, Y., Onabajo, M., Jung, I.-S., and Kim, Y.-B.: Accurate and efficient on-chip spectral analysis for built-in testing and calibration approaches, IEEE T. VLSI Syst., 22, 497–506, https://doi.org/10.1109/TVLSI.2013.2251919, 2013. a
Chen, W.-N., Zhang, J., Lin, Y., Chen, N., Zhan, Z.-H., Chung, H. S.-H., Li, Y., and Shi, Y.-H.: Particle swarm optimization with an aging leader and challengers, IEEE T. Evol. Comput., 17, 241–258, https://doi.org/10.1109/TEVC.2011.2173577, 2012. a
Daneshyari, M. and Yen, G. G.: Cultural-based multiobjective particle swarm optimization, IEEE T. Syst. Man Cybernet. Pt. B, 41, 553–567, https://doi.org/10.1109/TSMCB.2010.2068046, 2010. a
Delaine, F., Lebental, B., and Rivano, H.: In situ calibration algorithms for environmental sensor networks: A review, IEEE Sensors J., 19, 5968–5978, https://doi.org/10.1109/JSEN.2019.2910317, 2019. a
Diez-Olivan, A., Del Ser, J., Galar, D., and Sierra, B.: Data fusion and machine learning for industrial prognosis: Trends and perspectives towards Industry 4.0, Inform. Fusion, 50, 92–111, https://doi.org/10.1016/j.inffus.2018.10.005, 2019. a
Eberhart, R. and Kennedy, J.: A new optimizer using particle swarm theory, in: MHS'95, IEEE Proceedings of the Sixth International Symposium on Micro Machine and Human Science, 4–6 October 1995, Nagoya, Japan, 39–43, https://doi.org/10.1109/MHS.1995.494215, 1995. a
Hogervorst, R., Tero, J. P., Eschauzier, R. G., and Huijsing, J. H.: A compact power-efficient 3 V CMOS rail-to-rail input/output operational amplifier for VLSI cell libraries, IEEE J. Solid-state Circ., 29, 1505–1513, https://doi.org/10.1109/4.340424, 1994. a
Johns, D. A. and Martin, K.: Analog integrated circuit design, John Wiley & Sons, available at: https://www.wiley.com/en-us/Analog+Integrated+Circuit+Design,+2nd+Edition-p-9780470770108 (last access: 28 July 2021), 2008. a
Kagermann, H., Helbig, J., Hellinger, A., and Wahlster, W.: Recommendations for implementing the strategic initiative INDUSTRIE 4.0: Securing the future of German manufacturing industry, final report of the Industrie 4.0 Working Group, Forschungsunion, available at: http://thuvienso.dastic.vn:81/document.php?loc=0&doc=96250271808942028176694358165751814358 (last access: 17 August 2020), 2013. a
Kammara, A. C., Palanichamy, L., and König, A.: Multi-objective optimization and visualization for analog design automation, Complex Intel. Syst., 2, 251–267, https://doi.org/10.1007/s40747-016-0027-3, 2016. a
Kammara, A. C., Koenig, A., Graef, T., Chinazzo, A., Dobariya, C., Casper, F., Paul, J., Glenske, C., and Traute, J.: Co-Design of MR Sensor and Sensor Electronics for Self-X Integrated Sensory Systems, in: Sensors and Measuring Systems, 19th ITG/GMA-Symposium, VDE, 1–4, available at: https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=8436173 (last access: 12 August 2020), 2018a. a
Kammara, A. C., Pontes-Filho, S., and König, A.: Towards spiking neural systems synthesis, in: Control, Robotics and Sensors, Institution of Engineering & Technology https://doi.org/10.1049/PBCE119H_ch15, 2018b. a
Kennedy, J. and Mendes, R.: Population structure and particle swarm performance, in: vol. 2, IEEE Proceedings of the 2002 Congress on Evolutionary Computation, CEC'02 (Cat. No. 02TH8600), 12–17 May 2002, Honolulu, HI, USA, 1671–1676, https://doi.org/10.1109/CEC.2002.1004493, 2002. a
Koenig, A.: Integrated Sensor Electronics with Self-X Capabilities for Advanced Sensory Systems as a Baseline for Industry 4.0, in: Sensors and Measuring Systems, 19th ITG/GMA-Symposium, VDE, 1–4, available at: https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=8436169 (last access: 12 August 2020), 2018. a
Lee, J., Davari, H., Singh, J., and Pandhare, V.: Industrial Artificial Intelligence for industry 4.0-based manufacturing systems, Manufact. Lett., 18, 20–23, https://doi.org/10.1016/j.mfglet.2018.09.002, 2018a. a
Lee, S., Shi, C., Wang, J., Sanabria, A., Osman, H., Hu, J., and Sánchez-Sinencio, E.: A Built-In Self-Test and In Situ Analog Circuit Optimization Platform, IEEE TCAS I, 65, 3445–3458, https://doi.org/10.1109/TCSI.2018.2805641, 2018b. a, b, c
Li, D., Guo, W., Lerch, A., Li, Y., Wang, L., and Wu, Q.: An adaptive particle swarm optimizer with decoupled exploration and exploitation for large scale optimization, Swarm Evol. Comput., 60, 100789, https://doi.org/10.1016/j.swevo.2020.100789, 2021. a
Lin, L.-J.: Self-improving reactive agents based on reinforcement learning, planning and teaching, Mach. Learn., 8, 293–321, https://doi.org/10.1007/978-1-4615-3618-5_5, 1992. a
Lin, Y.-B., Lin, Y.-W., Lin, J.-Y., and Hung, H.-N.: SensorTalk: An IoT Device Failure Detection and Calibration Mechanism for Smart Farming, Sensors, 19, 4788, https://doi.org/10.3390/s19214788, 2019. a
Liu, W., Wang, Z., Liu, X., Zeng, N., and Bell, D.: A novel particle swarm optimization approach for patient clustering from emergency departments, IEEE T. Evol. Comput., 23, 632–644, https://doi.org/10.1109/TEVC.2018.2878536, 2018. a, b
Liu, W., Wang, Z., Yuan, Y., Zeng, N., Hone, K., and Liu, X.: A Novel Sigmoid-Function-Based Adaptive Weighted Particle Swarm Optimizer, IEEE T. Cybernet., 51, 1085–1093, https://doi.org/10.1109/TCYB.2019.2925015, 2019. a
Natarajan, V., Sen, S., Banerjee, A., Chatterjee, A., Srinivasan, G., and Taenzler, F.: Analog signature-driven postmanufacture multidimensional tuning of RF systems, IEEE Design Test Comput., 27, 6–17, https://doi.org/10.1109/MDT.2010.123, 2010. a, b
Picaut, J., Can, A., Fortin, N., Ardouin, J., and Lagrange, M.: Low-Cost Sensors for Urban Noise Monitoring Networks – A Literature Review, Sensors, 20, 2256, https://doi.org/10.3390/s20082256, 2020. a
Ratnaweera, A., Halgamuge, S. K., and Watson, H. C.: Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients, IEEE T. Evol. Comput., 8, 240–255, https://doi.org/10.1109/TEVC.2004.826071, 2004. a
Saeed, A., Elbably, M., Abdelfadeel, G., and Eladawy, M.: Efficient FPGA implementation of FFT/IFFT processor, Int. J. Circ. Syst. Sig. Process., 3, 103–110, 2009. a
Schaul, T., Quan, J., Antonoglou, I., and Silver, D.: Prioritized experience replay, arXiv preprint: arXiv:1511.05952, available at: https://arxiv.org/abs/1511.05952 (last access: 18 August 2020), 2015. a
Shi, C. and Sánchez-Sinencio, E.: 150–850 MHz high-linearity sine-wave synthesizer architecture based on FIR filter approach and SFDR optimization, IEEE T. Circ. Syst. I, 62, 2227–2237, https://doi.org/10.1109/TCSI.2015.2459552, 2015. a
Shi, Y. and Eberhart, R. C.: Empirical study of particle swarm optimization, in: vol. 3, IEEE Proceedings of the 1999 congress on evolutionary computation-CEC99 (Cat. No. 99TH8406), 6–9 July 1999, Washington, DC, USA, 1945–1950, https://doi.org/10.1109/CEC.1999.785511, 1999. a
Stoica, A.: Toward evolvable hardware chips: experiments with a programmable transistor array, in: IEEE Proceedings of the Seventh International Conference on Microelectronics for Neural, Fuzzy and Bio-Inspired Systems, 9 April 1999, Granada, Spain, 156–162, https://doi.org/10.1109/MN.1999.758859, 1999. a
Stoica, A., Zebulum, R., and Keymeulen, D.: Mixtrinsic evolution, in: International Conference on Evolvable Systems, Springer, 208–217, https://doi.org/10.1007/3-540-46406-9_21, 2000. a
Stratigopoulos, H.-G. and Mir, S.: Adaptive alternate analog test, IEEE Design Test Comput., 29, 71–79, https://doi.org/10.1109/MDT.2012.2205480, 2012. a, b
Sutton, R. S. and Barto, A. G.: Reinforcement learning: An introduction, MIT Press, 2018. a
Tawdross, P. M. M.: Bio-inspired circuit sizing and trimming methods for dynamically reconfigurable sensor electronics in industrial embedded systems, available at: http://nbn-resolving.de/urn:nbn:de:hbz:386-kluedo-21516 (last access: 11 March 2019), 2007. a, b
Trends, S.: Trends in future-oriented sensor technologies, AMA Association for Sensor Technology, Berlin, Germany, available at: https://www.ama-sensorik.de/fileadmin/Pubikationen/AMA_Study_Sensor_Trends%5b1%5d.pdf (last access: 23 May 2019), 2014. a
Variyam, P. N., Cherubal, S., and Chatterjee, A.: Prediction of analog performance parameters using fast transient testing, IIEEE TCAD, 21, 349–361, https://doi.org/10.1109/43.986428, 2002. a, b, c
Vural, R. and Yildirim, T.: Analog circuit sizing via swarm intelligence, AEU – Int. J. Eelect. Commun., 66, 732–740, https://doi.org/10.1016/j.aeue.2012.01.003, 2012. a
Wei, C.-L., Wang, Y.-W., and Liu, B.-D.: Wide-range filter-based sinusoidal wave synthesizer for electrochemical impedance spectroscopy measurements, IEEE T. Biomed. Circ. Syst., 8, 442–450, https://doi.org/10.1109/TBCAS.2013.2274100, 2013. a
Yang, C. and Mason, A. J.: Fully integrated seven-order frequency-range quadrature sinusoid signal generator, IEEE T. Instrum. Meas., 58, 3481–3489, https://doi.org/10.1109/TIM.2009.2018001, 2009. a
Ye, L., Shi, C., Liao, H., Huang, R., and Wang, Y.: Highly power-efficient active-RC filters with wide bandwidth-range using low-gain push-pull opamps, IEEE T. Circ. Syst. I, 60, 95–107, https://doi.org/10.1109/TCSI.2012.2215700, 2012. a
Zaman, Q. and König, A.: Self-x integrated sensor circuits immune to measurement noise in the presence of input perturbation by using robust optimization/Integrierte Sensorelektronik mit Self-x-Eigenschaften und verbesserter Immunität gegenüber Rauscheinflüssen bei der Messung und Störung der Eingangsgrößen durch ein robustes Optimierungsverfahren, tm – Technisches Messen, 86, 107–111, https://doi.org/10.1515/teme-2019-0053, 2019. a
Zaman, Q., Alraho, S., and König, A.: Low-cost Indirect Measurement Methods for Self-x Integrated Sensory Electronics for Industry 4.0, tm – Technisches Messen, 87, s79–s84, https://doi.org/10.1515/teme-2020-0020, 2020a. a
Zaman, Q., Alraho, S., and König, A.: Robust Optimization of Self-x Sensory Electronics in Presences of Environmental Variations for Industry 4.0, SMSI – Sensor and Measurement SMSI Science International, 295–296, https://doi.org/10.5162/SMSI2020/D5.2, 2020b. a
Zeng, N., Zhang, H., Chen, Y., Chen, B., and Liu, Y.: Path planning for intelligent robot based on switching local evolutionary PSO algorithm, J. Assembly Automat., 36, 120–126, https://doi.org/10.1108/AA-10-2015-079, 2016. a, b
Zeng, N., Wang, Z., Liu, W., Zhang, H., Hone, K., and Liu, X.: A Dynamic Neighborhood-Based Switching Particle Swarm Optimization Algorithm, IEEE T. Cybernet., https://doi.org/10.1109/TCYB.2020.3029748, 2020. a
Zhan, Z.-H., Zhang, J., Li, Y., and Chung, H. S.-H.: Adaptive particle swarm optimization, IEEE T. Syst. Man Cybernet. Pt. B, 39, 1362–1381, https://doi.org/10.1109/TSMCB.2009.2015956, 2009. a, b