Aeroacoustic analysis using natural Helmholtz–Hodge decomposition

The analysis of aeroacoustic phenomena is crucial for a deeper understanding of the damping mechanisms of a sound-absorbing bias flow liner (BFL). For this purpose, simultaneous measurements of the sound field and the flow field in a BFL are required. The fluid velocity can serve as the measurand, where both the acoustic particle velocity and the aerodynamic flow velocity contribute and, thus, can be acquired simultaneously. However, there is a need to separate these two quantities to distinguish between them. This is challenging because they generally coincide with each other in the time domain. Due to the interaction of sound and flow in a BFL, both velocities also overlap in the temporal frequency domain, having a coherent oscillation at the acoustic frequency. For this reason, the recently developed natural Helmholtz–Hodge decomposition (NHHD) is applied to separate both quantities from the measured oscillation velocity field in the spatial domain. The evaluation of synthetic vector field data shows that the quality of the decomposition is enhanced when a smaller grid size is chosen. The velocity field in a generic BFL, necessarily recorded within a three-dimensional region of interest at more than 4000 measurement locations, is evaluated using NHHD. As a result, the measured oscillation velocity in the BFL is dominated by the flow that is related to vortices and also by irrotational aerodynamic flow. Moreover, indications for an aeroacoustic source near the facing sheet of the liner are revealed.

1 Introduction

In order to improve the efficiency of modern aeroacoustic noise absorbers in aircraft engines, a deeper understanding of the underlying damping phenomena is necessary, according to Zhao and Li (2015). Therefore, an enhanced knowledge about the interaction between flow and sound in noise absorbers has to be obtained. Since the effort of a direct numerical simulation is too excessive, simultaneous measurements of the flow field and the sound field are needed as a prerequisite for an aeroacoustic analysis. The choice of optical measurement methods is advantageous, since these methods are usually contactless and, thus, do not alter the measured field. The measurement of the fluid velocity is beneficial concerning the simultaneous acquisition of both the (aerodynamic) flow velocity and the acoustic particle velocity, since both are included in the measurand. However, the separation of both quantities is impossible in the time domain because both coincide with each other at the velocity signal in the temporal domain. A separation in the temporal frequency domain is also challenging, since the flow velocity also oscillates at acoustic frequencies. Such an oscillation occurs due to an interaction of the flow and the sound wave. As an example, this interaction is analyzed in a bias flow liner in this paper. A bias flow liner is a perforated acoustic liner with an additional flow through the perforation; see Heuwinkel et al. (2010). Thus, the scientific question arises: can the decomposition of the oscillating fluid velocity field, measured in a bias flow liner, into the flow velocity field and the acoustic particle velocity field, which is impossible in both the time domain and the temporal frequency domain, be performed in the spatial domain?

Previous separation approaches using the Proper Orthogonal Decomposition (POD) of the measured velocity field, like in Rupp et al. (2010) and Marx et al. (2010), suffer from ambiguities; i.e., it is unclear whether the resulting modes are related to the flow field or the sound field. Unlike the POD, the Helmholtz–Hodge decomposition (HHD) provides the separation between the solenoidal (divergence-free) flow velocity field and the irrotational (curl-free) acoustic particle velocity field for Mach numbers below 0.3; cf. De Roeck et al. (2007). However, the unique calculation HHD relies on the assumption of boundary conditions, which are typically not (exactly) known. To overcome this difficulty, an enhanced method, called natural Helmholtz–Hodge decomposition (NHHD) from Bhatia et al. (2014), has been developed recently, where the flow field is separated into internal (known) and external (unknown) components and, thus, no flow-dependent boundary conditions have to been chosen, though they result from the separation. Since the NHHD has been applied neither to experimental data nor in aeroacoustics at all before, the application of this method is discussed in this paper for the example of measurements in a generic bias flow liner. The paper is structured as follows: first, the NHHD method is explained and its implementation is presented in Sect. 2. Afterwards, the verification of this implementation and the characterization of the NHHD method for the aeroacoustic application based on synthetic data is performed in Sect. 3. Next, the NHHD is applied to separate the acoustic particle velocity and the aerodynamic flow velocity from the fluid velocity measured in a bias flow liner. This application of the NHHD is demonstrated and the analysis results are discussed in Sect. 4. Finally, the paper is closed with a conclusion in Sect. 5, including an outlook for future investigations.

2 Method

To split a spatially bounded vector field into its solenoidal and its irrotational part, the conventional HHD has previously been applied in many research fields, including fluid mechanics, by Denaro (2003), Rousseaux et al. (2007), and Galvin et al. (2012). A comprehensive overview of application fields and a history outline have already been given by Bhatia et al. (2013). When using the HHD, however, boundary conditions have to be known or at least assumed in order to ensure a unique solution. This results in calculation errors if the assumptions for the boundaries are inaccurate or incorrect. Consequently, artifacts in the decomposed velocity data set will occur for a given measured velocity field with unknown boundary conditions. In contrast, the idea of the NHHD, according to Bhatia et al. (2014), is to distinguish between internal and external influences of the vector field, determined by the measured field and resulting from the (unknown) exterior field, respectively. Thus, the NHHD method eliminates the need for flow-dependent boundary conditions to uniquely decompose the measured field. This decomposition of a given vector field is termed natural, since the complete information that is necessary is contained in the given vector data itself. Hence, further knowledge about the exterior field is not required, nor do any (potentially invalid) assumptions about the boundary conditions have to be made. One minor drawback for the application of the NHHD is that orthogonality of the decomposed fields cannot be guaranteed (in contrast to the conventional HHD using boundary conditions), which may provoke higher errors in numerical simulations; however, orthogonality is not required for the analysis of data, in accordance with Bhatia et al. (2014).

In the following paragraphs, the theoretical aspects of the NHHD from Bhatia et al. (2014) and its implementation details used for the subsequent Sects. 3 and 4 are briefly introduced.

2.1 Theory

According to the ideas of Helmholtz (1858), every spatially unbounded, simply connected vector field $\mathit{V}:{\mathbb{R}}^n⟶{\mathbb{R}}^n$ for $n=\mathrm{2},\mathrm{3}$ that vanishes at infinity can be decomposed into a sum of an irrotational divergent term

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle }\mathit{d}=\mathrm{\nabla }D\text{ with }\mathrm{\nabla }\times \mathit{d}=\mathbf{0},\end{array}$$

related to the scalar potential D, and a solenoidal rotational term

$$\begin{array}{llll}{\displaystyle }& {\displaystyle }\mathit{r}=J\mathrm{\nabla }R& {\displaystyle }& {\displaystyle }\text{in }{\mathbb{R}}^{\mathrm{2}}\text{ with }\mathrm{\nabla }\cdot \mathit{r}=\mathrm{0},\\ \text{(2)}& {\displaystyle }& {\displaystyle }\mathit{r}=\mathrm{\nabla }\times \mathit{R}& {\displaystyle }& {\displaystyle }\text{in }{\mathbb{R}}^{\mathrm{3}}\text{ with }\mathrm{\nabla }\cdot \mathit{r}=\mathrm{0},\end{array}$$

where

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle }J=\left(\begin{array}{cc}\cos \mathit{\theta }& -\sin \mathit{\theta }\\ \sin \mathit{\theta }& \cos \mathit{\theta }\end{array}\right)\text{with }\mathit{\theta }={\displaystyle \frac{\mathit{\pi }}{\mathrm{2}}}\end{array}$$

is the π∕2-rotation operator, R is a scalar potential, and R a vector potential. As a consequence, the divergence and curl of the vector field V in a convex domain are completely represented by the divergence of d and curl of r, i.e.,

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle }\mathrm{\nabla }\cdot \mathit{d}={\mathrm{\nabla }}^{\mathrm{2}}D=\mathrm{\nabla }\cdot \mathit{V}\text{in }{\mathbb{R}}^n\end{array}$$

and

$$\begin{array}{llll}{\displaystyle }& {\displaystyle }\mathrm{\nabla }\times \mathit{r}=\mathrm{\nabla }\cdot (-J\mathit{r})={\mathrm{\nabla }}^{\mathrm{2}}R=\mathrm{\nabla }\times \mathit{V}& {\displaystyle }& {\displaystyle }\text{in }{\mathbb{R}}^{\mathrm{2}},\\ \text{(5)}& {\displaystyle }& {\displaystyle }\mathrm{\nabla }\times \mathit{r}=-{\mathrm{\nabla }}^{\mathrm{2}}\mathit{R}=\mathrm{\nabla }\times \mathit{V}& {\displaystyle }& {\displaystyle }\text{in }{\mathbb{R}}^{\mathrm{3}},\end{array}$$

where ∇² is the (scalar) Laplacian (if ℝ²) or the vector Laplacian (if ℝ³). If a spatially bounded vector field $\mathit{v}\left(\stackrel{\mathrm{̃}}{\mathit{s}}\right):\mathrm{\Omega }⟶{\mathbb{R}}^n$ for $n=\mathrm{2},\mathrm{3}$ and the convex spatial domain Ω⊂ℝⁿ is considered such that $\mathit{V}\left(\stackrel{\mathrm{̃}}{\mathit{s}}\right)=\mathit{v}\left(\stackrel{\mathrm{̃}}{\mathit{s}}\right)$ for all position vectors $\stackrel{\mathrm{̃}}{\mathit{s}}\in \mathrm{\Omega }$, a harmonic term

$$\begin{array}{}\text{(6)}& {\displaystyle }{\displaystyle }\mathit{h}=\mathit{v}-\mathit{d}-\mathit{r}\text{with }\mathrm{\nabla }\times \mathit{h}=\mathbf{0}\text{ and }\mathrm{\nabla }\cdot \mathit{h}=\mathrm{0}\end{array}$$

may remain that is both irrotational and solenoidal, following Bhatia et al. (2014).

Performing the NHHD means calculating the divergent term d and the rotational term r inside the domain Ω using a unique solution of the Poisson Eqs. (4) and (5) for both potential fields (D and R or R) using the given vector field v. The potential fields

$$\begin{array}{llll}{\displaystyle }D\left(\mathit{s}\right)& {\displaystyle }=\underset{\mathrm{\Omega }}{\int }{G}_{\mathrm{\infty }}\left(\mathit{s},\stackrel{\mathrm{̃}}{\mathit{s}}\right)\mathrm{\nabla }\cdot \mathit{v}\left(\stackrel{\mathrm{̃}}{\mathit{s}}\right)\mathrm{d}\stackrel{\mathrm{̃}}{\mathit{s}}& {\displaystyle }& {\displaystyle }\\ {\displaystyle }& {\displaystyle }+\underset{{\mathbb{R}}^n\backslash \mathrm{\Omega }}{\int }{G}_{\mathrm{\infty }}\left(\mathit{s},\stackrel{\mathrm{̃}}{\mathit{s}}\right)\mathrm{\nabla }\cdot \mathit{V}\left(\stackrel{\mathrm{̃}}{\mathit{s}}\right)\mathrm{d}\stackrel{\mathrm{̃}}{\mathit{s}}& {\displaystyle }& {\displaystyle }\text{in }{\mathbb{R}}^n\end{array}$$

and

$$\begin{array}{ll}{\displaystyle }R\left(\mathit{s}\right)& {\displaystyle }=\underset{\mathrm{\Omega }}{\int }{G}_{\mathrm{\infty }}\left(\mathit{s},\stackrel{\mathrm{̃}}{\mathit{s}}\right)\mathrm{\nabla }\times \mathit{v}\left(\stackrel{\mathrm{̃}}{\mathit{s}}\right)\mathrm{d}\stackrel{\mathrm{̃}}{\mathit{s}}\\ {\displaystyle }& {\displaystyle }+\underset{{\mathbb{R}}^n\backslash \mathrm{\Omega }}{\int }{G}_{\mathrm{\infty }}\left(\mathit{s},\stackrel{\mathrm{̃}}{\mathit{s}}\right)\mathrm{\nabla }\times \mathit{V}\left(\stackrel{\mathrm{̃}}{\mathit{s}}\right)\mathrm{d}\stackrel{\mathrm{̃}}{\mathit{s}}& {\displaystyle }& {\displaystyle }\text{in }{\mathbb{R}}^{\mathrm{2}},\\ {\displaystyle }\mathit{R}\left(\mathit{s}\right)& {\displaystyle }=-\underset{\mathrm{\Omega }}{\int }{G}_{\mathrm{\infty }}\left(\mathit{s},\stackrel{\mathrm{̃}}{\mathit{s}}\right)\mathrm{\nabla }\times \mathit{v}\left(\stackrel{\mathrm{̃}}{\mathit{s}}\right)\mathrm{d}\stackrel{\mathrm{̃}}{\mathit{s}}\\ \text{(7)}& {\displaystyle }& {\displaystyle }-\underset{{\mathbb{R}}^n\backslash \mathrm{\Omega }}{\int }{G}_{\mathrm{\infty }}\left(\mathit{s},\stackrel{\mathrm{̃}}{\mathit{s}}\right)\mathrm{\nabla }\times \mathit{V}\left(\stackrel{\mathrm{̃}}{\mathit{s}}\right)\mathrm{d}\stackrel{\mathrm{̃}}{\mathit{s}}& {\displaystyle }& {\displaystyle }\text{in }{\mathbb{R}}^{\mathrm{3}},\end{array}$$

result, where G_∞ is the free-space Green's function (cf. Bhatia et al., 2014), which is a fundamental solution of the Poisson Eqs. (4) and (5) and reads

$$\begin{array}{llll}{\displaystyle }& {\displaystyle }{G}_{\mathrm{\infty }}\left(\mathit{s},\stackrel{\mathrm{̃}}{\mathit{s}}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }}}\ln \left(\left|\stackrel{\mathrm{̃}}{\mathit{s}}-\mathit{s}\right|\right)& {\displaystyle }& {\displaystyle }\text{in }{\mathbb{R}}^{\mathrm{2}}\\ {\displaystyle }& {\displaystyle }\text{or}\\ \text{(8)}& {\displaystyle }& {\displaystyle }{G}_{\mathrm{\infty }}\left(\mathit{s},\stackrel{\mathrm{̃}}{\mathit{s}}\right)=-{\displaystyle \frac{\mathrm{1}}{\mathrm{4}\mathit{\pi }\left|\stackrel{\mathrm{̃}}{\mathit{s}}-\mathit{s}\right|}}& {\displaystyle }& {\displaystyle }\text{in }{\mathbb{R}}^{\mathrm{3}},\end{array}$$

for two-dimensional or three-dimensional problems, respectively. Following Bhatia et al. (2014) the solution of Eqs. (4) and (5) can be achieved under the approximation that the integral ${\int }_{{\mathbb{R}}^n\backslash \mathrm{\Omega }}\left(\mathrm{\dots }\right)$ can be neglected since it only contributes to the harmonic flow inside Ω. Hence, using the NHHD requires no knowledge of the flow field outside Ω, since its contribution is neglected for any unknown field V and, thus, no flow dependent boundary conditions have to be chosen. After calculating d and r using Eqs. (1) and (2), h can be finally obtained using Eq. (6). Note that NHHD enables the determination whether a harmonic flow is present or not.

2.2 Implementation

The NHHD algorithm from Sect. 2.1 is implemented in MATLAB^®. For three-dimensional problems, the input data consist of a three-dimensional vector field $\mathit{v}={\left(v_x,v_y,v_z\right)}^{\mathrm{T}}$ of three vector components v_x, v_y, and v_z, regarding the Cartesian coordinate system given by the x, y, and z coordinates. The calculation of the derivatives in Eq. (7) is approximated by central finite differences. For the sake of simplicity, this approximation is given as an example for a two-dimensional vector field v:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{\nabla }\cdot \mathit{v}\left(\stackrel{\mathrm{̃}}{\mathit{s}}\right)\approx \\ {\displaystyle }& {\displaystyle \frac{v_x\left(\begin{array}{c}\stackrel{\mathrm{̃}}{x}+\mathit{\delta }s\\ \stackrel{\mathrm{̃}}{y}\end{array}\right)-v_x\left(\begin{array}{c}\stackrel{\mathrm{̃}}{x}-\mathit{\delta }s\\ \stackrel{\mathrm{̃}}{y}\end{array}\right)+v_y\left(\begin{array}{c}\stackrel{\mathrm{̃}}{x}\\ \stackrel{\mathrm{̃}}{y}+\mathit{\delta }s\end{array}\right)-v_y\left(\begin{array}{c}\stackrel{\mathrm{̃}}{x}\\ \stackrel{\mathrm{̃}}{y}-\mathit{\delta }s\end{array}\right)}{\mathrm{2}\mathit{\delta }s}}\end{array}$$

and

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{\nabla }\times \mathit{v}\left(\stackrel{\mathrm{̃}}{\mathit{s}}\right)\approx \\ \text{(9)}& {\displaystyle }& {\displaystyle \frac{v_y\left(\begin{array}{c}\stackrel{\mathrm{̃}}{x}+\mathit{\delta }s\\ \stackrel{\mathrm{̃}}{y}\end{array}\right)-v_y\left(\begin{array}{c}\stackrel{\mathrm{̃}}{x}-\mathit{\delta }s\\ \stackrel{\mathrm{̃}}{y}\end{array}\right)-v_x\left(\begin{array}{c}\stackrel{\mathrm{̃}}{x}\\ \stackrel{\mathrm{̃}}{y}+\mathit{\delta }s\end{array}\right)+v_x\left(\begin{array}{c}\stackrel{\mathrm{̃}}{x}\\ \stackrel{\mathrm{̃}}{y}-\mathit{\delta }s\end{array}\right)}{\mathrm{2}\mathit{\delta }s}},\end{array}$$

where δs is the grid size on a regular grid of discrete positions $\stackrel{\mathrm{̃}}{\mathit{s}}={\left(\stackrel{\mathrm{̃}}{x},\stackrel{\mathrm{̃}}{y}\right)}^{\mathrm{T}}$ of the vector data. The numerical integration, as an approximation of the Eq. (7), is accomplished using the rectangle method (Riemann sum). Again, the approximation is given as an example for a two-dimensional vector field v:

$${\displaystyle }{\displaystyle }D\left(\mathit{s}\right)\approx \sum _{\stackrel{\mathrm{̃}}{\mathit{s}}\in \mathrm{\Omega }}{G}_{\mathrm{\infty }}\left(\mathit{s},\stackrel{\mathrm{̃}}{\mathit{s}}\right)\mathrm{\nabla }\cdot \mathit{v}\left(\stackrel{\mathrm{̃}}{\mathit{s}}\right){\left(\mathit{\delta }s\right)}^{\mathrm{2}}$$

and

$$\begin{array}{}\text{(10)}& {\displaystyle }{\displaystyle }R\left(\mathit{s}\right)\approx \sum _{\stackrel{\mathrm{̃}}{\mathit{s}}\in \mathrm{\Omega }}{G}_{\mathrm{\infty }}\left(\mathit{s},\stackrel{\mathrm{̃}}{\mathit{s}}\right)\mathrm{\nabla }\times \mathit{v}\left(\stackrel{\mathrm{̃}}{\mathit{s}}\right){\left(\mathit{\delta }s\right)}^{\mathrm{2}}\end{array}$$

for the position vector $\mathit{s}={\left(x,y\right)}^{\mathrm{T}}$, by means of summation of the expressions from Eq. (9) over each vector $\stackrel{\mathrm{̃}}{\mathit{s}}$ within the spatial region Ω. Note that a special treatment of Eq. (10) is necessary in the case of $\stackrel{\mathrm{̃}}{\mathit{s}}=\mathit{s}$, where the value G_∞ of the Green's function from Eq. (8) converges to −∞. Here, the corresponding value G_∞ is arbitrarily set to zero, which means that this particular value is excluded from the integration.

3 Qualification

In order to verify the implementation from Sect. 2.2 and characterize the method presented in Sect. 2.1, exemplary tests using synthetic data are performed. For the sake of simplicity of the visualization, the test results are presented for two-dimensional data only.

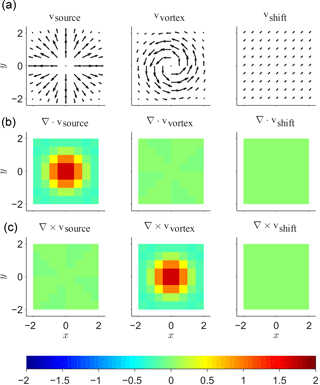
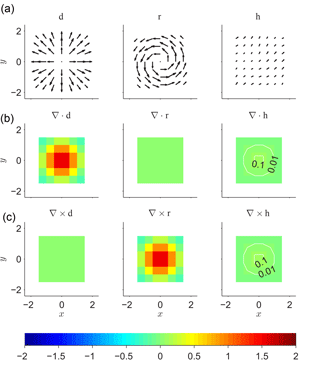
Figure 1 Synthetic input vector field terms (a), the corresponding divergence (b) and curl (c), depicted for field data with a grid size of $\mathit{\delta }s=\mathrm{1}/\mathrm{2}$.

3.1 Database

A synthetic two-dimensional vector field with a quantity of dimension one is selected as input data for the NHHD algorithm. The original (Euclidean) vector field

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathit{v}={\mathit{v}}_{\text{source}}+{\mathit{v}}_{\text{vortex}}+{\mathit{v}}_{\text{shift}}\text{ with}\\ {\displaystyle }& {\displaystyle }{\mathit{v}}_{\text{source}}={\left(x,y\right)}^{\mathrm{T}}\cdot \exp \left[-\mathrm{0.5}\left(x^{\mathrm{2}}+y^{\mathrm{2}}\right)\right],\\ {\displaystyle }& {\displaystyle }{\mathit{v}}_{\text{vortex}}={\left(-y,x\right)}^{\mathrm{T}}\cdot \exp \left[-\mathrm{0.5}\left(x^{\mathrm{2}}+y^{\mathrm{2}}\right)\right],\text{ and}\\ \text{(11)}& {\displaystyle }& {\displaystyle }{\mathit{v}}_{\text{shift}}=\left(\mathrm{0.1},\mathrm{0.1}\right)\end{array}$$

is a sum of exemplary terms, which are visualized in Fig. 1a, with a grid size of $\mathit{\delta }s=\mathrm{1}/\mathrm{2}$ regarding the Cartesian coordinates x and y. According to the analytic expressions in Eq. (11), the source term v_source in Eq. (11) has no curl (i.e., $\mathrm{\nabla }\times {\mathit{v}}_{\text{source}}=\mathrm{0}$) and the vortex term v_vortex has no divergence (i.e., $\mathrm{\nabla }\cdot {\mathit{v}}_{\text{vortex}}=\mathrm{0}$). Given these fields, the source term is representative of an acoustic field (spherical wave) and the vortex term is representative of a rotational aerodynamic flow field. The shift term v_shift has neither curl nor divergence (i.e., $\mathrm{\nabla }\times {\mathit{v}}_{\text{shift}}=\mathrm{\nabla }\cdot {\mathit{v}}_{\text{shift}}=\mathrm{0}$) and represents an irrotational aerodynamic flow. Since v_shift is solenoidal, it cannot be related to the acoustic field because of its compressibility by definition. There are also nontrivial vector fields that have the same properties as v_shift, which are not considered here further. Note that the exemplary terms were chosen such that their divergence or curl has a (preferably representative) inhomogeneous spatial distribution, which was realized by exponential functions in Eq. (11).

For comparison with the output vector field terms in the following subsection, the divergence and curl of the input vector field terms are calculated numerically using central finite differences; cf. Eq. (9). The resulting divergence and curl are depicted in Fig. 1b and c as well. The numerical result has slight deviations below 10⁻² from the analytic result due to the discretization of the vector field terms and the approximation in Eq. (9). Note that the original field from Eq. (11) is free from noise terms, which can, however, be easily included in the synthetic data. As a consequence, the noise will be independently decomposed into irrotational, solenoidal, and harmonic terms due to the linearity of the NHHD. However, the focus of this paper is an initial quantitative characterization of the NHHD in the first place.

Figure 2 Output vector fields (a), as well as the corresponding divergence (b) and curl (c) using the natural Helmholtz–Hodge decomposition of the synthetic vector field from Eq. (11); cf. Fig. 1 for a grid size of $\mathit{\delta }s=\mathrm{1}/\mathrm{2}$.

3.2 Characterization

Using its implementation according to Sect. 2.2, the NHHD algorithm is applied to the input data base v from Eq. (11); see Sect. 3.1. Assuming an ideal decomposition following Sect. 2.1, the resulting output vector fields consequently read

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathit{d}={\mathit{v}}_{\text{source}},\\ {\displaystyle }& {\displaystyle }\mathit{r}={\mathit{v}}_{\text{vortex}}\text{, and}\\ \text{(12)}& {\displaystyle }& {\displaystyle }\mathit{h}={\mathit{v}}_{\text{shift}}.\end{array}$$

The actual result of the NHHD is depicted in Fig. 2 for field data of d,r, and h with a grid size of $\mathit{\delta }s=\mathrm{1}/\mathrm{2}$, as well as the corresponding divergence and curl. In the resulting output field, there are no vector data at the outermost positions due to the double use of central finite differences for the approximation of the derivatives both in Eqs. (1)–(6) and in Eq. (7). Notwithstanding, according to Eq. (12), Fig. 2 should be identical to Fig. 1 in the case of an ideal decomposition. In fact, there are (minor) deviations from the expectation; e.g., in particular, the term h does not completely agree with the input vector field term v_shift from Eq. (12). In addition, both divergence and curl of h are not exactly zero, which is contrary to the characteristic properties defined in Eq. (6). Since these deviations were not discussed before by Bhatia et al. (2014), they are investigated in the following. In order to characterize these deviations, the term crosstalk is used in the following as a figure of merit. Typically, the crosstalk is defined as the squared ratio of the root mean square of the undesired signal to the root mean square of another adjacent signal. Following that,

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\text{crosstalk}}_{\mathbf{\nabla }\cdot \mathit{h}}={\displaystyle \frac{\sum _{\mathit{s}\in \mathrm{\Omega }}{\left|\mathbf{\nabla }\cdot \mathit{h}\left(\mathit{s}\right)\right|}^{\mathrm{2}}}{\sum _{\mathit{s}\in \mathrm{\Omega }}{\left|\mathbf{\nabla }\cdot \mathit{v}\left(\mathit{s}\right)\right|}^{\mathrm{2}}}}\text{ and }\\ \text{(13)}& {\displaystyle }& {\displaystyle }{\text{crosstalk}}_{\mathbf{\nabla }\times \mathit{h}}={\displaystyle \frac{\sum _{\mathit{s}\in \mathrm{\Omega }}{\left|\mathbf{\nabla }\times \mathit{h}\left(\mathit{s}\right)\right|}^{\mathrm{2}}}{\sum _{\mathit{s}\in \mathrm{\Omega }}{\left|\mathbf{\nabla }\times \mathit{v}\left(\mathit{s}\right)\right|}^{\mathrm{2}}}}\end{array}$$

are defined regarding the parasitic divergence and curl of the harmonic signal h relating to the divergence and the curl of the input vector field v, respectively, within the complete set of the region Ω.

Figure 3 Resulting crosstalk, according to Eq. (13) as a quality factor of the natural Helmholtz–Hodge decomposition, when applied to the synthetic input vector field from Eq. (11) for several grid sizes δs of the vector field.

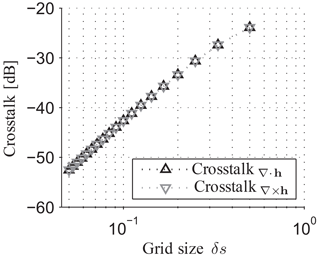
The crosstalk from Eq. (13) in Fig. 2 is investigated for several grid sizes δs of the vector field; cf. Figure 3. In Fig. 2, crosstalk_∇⋅h and crosstalk_∇×h are identical for the exemplary terms chosen here. A smaller grid size obviously leads to a lower crosstalk; a decrease of up to 30 dB per decade can be achieved. This behavior can be explained by the fact that computational errors of the spatial derivatives in Eqs. (1)–(7) that are approximated by Eq. (9) using finite difference quotients increase when the grid size is enlarged. Although not being investigated further, a qualitatively similar observation is expected for three-dimensional problems as well.

4 Application

In order to obtain experimental data for the aeroacoustic analysis, an optical measurement of the velocity vector field in a generic bias flow liner is performed using frequency-modulated Doppler global velocimetry (FM-DGV) from Haufe et al. (2013). In contrast to previous measurements by Haufe et al. (2013), here, a set of three-dimensional velocity vector data is gathered in order to apply the NHHD, since a three-dimensional problem is expected for the vector field in the bias flow liner. For the experiments, FM-DGV offers a high dynamic range of more than 3 orders of magnitude; see Haufe et al. (2013). Moreover, the velocity uncertainty is nearly identical for all vector components (see Sect. 4.1.2), which is in contrast to other optical methods like stereoscopic particle image velocimetry. Apart from that, any other measurement method providing volumetric velocity vector data can be considered for the evaluation using NHHD. In any case, time-resolved or phase-resolved velocity data (when the region of interest is successively scanned, like here) are necessary since time-averaged values do not contain any acoustic information.

4.1 Experimental setup

4.1.1 Aeroacoustics

The aeroacoustic experiment in a generic bias flow liner is conducted in Berlin at the “Duct acoustic test rig with rectangular cross section” (DUCT-R), which is about 3 m long. The DUCT-R has anechoic terminations at both ends and has a cross section of 60 mm×80 mm (inner dimensions). Flow and sound are generated under ambient conditions by a radial compressor and a Monacor speaker KU-516, respectively. The mean flow velocity is set to approximately 34 m s⁻¹ (corresponding to Mach 0.1 and a mean mass flow rate of about 700 kg h⁻¹) with a turbulence intensity of about 7 %. The sound pressure level of the incident acoustic wave is about 118 dB for the sinusoidal excitation at a frequency of 1122 Hz, where the liner exhibits its maximum dissipation coefficient of about 60 %, according to a previous study on the same liner by Schulz et al. (2015).

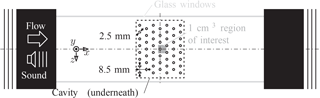
Figure 4 Top view of the setup of the aeroacoustic measurement in a generic bias flow liner with optical access through glass windows; the point of origin is at the center of the central orifice.

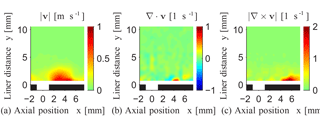
Figure 5 (a) Measured input vector field, i.e., phase-averaged oscillation velocity v, (b) its divergence ∇⋅v, and (c) curl ∇×v for a selected phase φ=2π at the lateral position z=0 (see Fig. 4); vectorial quantities are depicted regarding their l² norm.

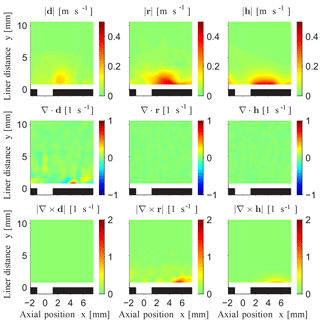
Figure 6 Output vector fields (l² norm) at the lateral position z=0, when applying the natural Helmholtz–Hodge decomposition on the measured phase-averaged oscillation velocity v for a selected phase φ=2π from Fig. 5a as input vector field, using a grid size of δs≈0.04 mm.

The design of the bias flow liner is based on previous work by Heuwinkel et al. (2010); see Fig. 4. The perforation is composed of a 1 mm thick facing sheet with 53 circular orifices, each with a diameter of 2.5 mm and a distance of 8.5 mm. The only difference of this liner to the one investigated by Heuwinkel et al. (2010) is that the cross section is rectangular in order to match with DUCT-R. The cavity is a cuboid with a size of $\mathrm{60}\mathrm{mm}\times \mathrm{49}\mathrm{mm}\times \mathrm{72}\mathrm{mm}$ (in the direction of x, y, and z). A bias flow with a mass flow rate of 5 kg h⁻¹ is fed into the cavity. This value corresponds to an estimated bias flow velocity, according to Heuwinkel et al. (2010), of about 7 m s⁻¹ at vena contracta, where an equal distribution of the mass flow through the orifices and an empirically found jet contraction factor of 0.61 is assumed. The resulting Reynolds number of the bias flow is about 10³, assuming dry air at 20 ^∘C and the diameter of the orifice as the characteristic length.

4.1.2 Metrology

The velocity data are measured by FM-DGV at eight locations in parallel, linearly arranged in y direction, as described in detail by Haufe et al. (2013). For this purpose, tracer particles made of diethylhexyl sebacate with a diameter of about 1 µm and a response time of 3,4 µs (see Albrecht et al. (2003)), corresponding to a slippage of less than 0.1 % at 1122 Hz, are added to the fluid. A measurement frequency of 100 kHz is chosen, which is a typical choice for the FM-DGV system and (more than) sufficiently large to resolve the acoustic frequency, regarding the sampling theorem. In order to achieve a volumetric acquisition, successive linear traversing in the direction of x, y, and z is used for 16, 2, and 16 positions. This results in a large number of 16³=4096 locations on a regular grid; the spatial resolution is about 0.6 mm in each direction x, y, and z. The minimal distance to the perforation was at y≈0.8 mm. The chosen region of interest is a cube with a volume of 1 cm³ in the vicinity of the central orifice, where the optical access is provided through glass windows. The laser light enters the region of interest along the incidence vector $\mathit{i}=(\mathrm{0},-\mathrm{1},\mathrm{0}{)}^{\mathrm{T}}$, is scattered by the tracer particles, and is finally observed in three different directions, along the observation vectors ${\mathit{o}}_{\mathrm{1}}=\left(\sin \right[\mathrm{35}{}^{\circ }],\mathrm{0},\cos [\mathrm{35}{}^{\circ }]{)}^{\mathrm{T}}$, ${\mathit{o}}_{\mathrm{2}}=(-\sin [\mathrm{35}{}^{\circ }],\mathrm{0},-\cos [\mathrm{35}{}^{\circ }]{)}^{\mathrm{T}}$ and ${\mathit{o}}_{\mathrm{3}}=\left(\sin \right[\mathrm{35}{}^{\circ }],\mathrm{0},-\cos [\mathrm{35}{}^{\circ }]{)}^{\mathrm{T}}$, which gives three (non-Cartesian) velocity components $v_{{\mathit{o}}_{\mathrm{1}}-i}$, $v_{{\mathit{o}}_{\mathrm{2}}-i}$, and $v_{{\mathit{o}}_{\mathrm{3}}-i}$, each along the vectors o₁−i, o₂−i, and o₃−i, respectively. The Cartesian velocity vector $\mathit{v}=(v_x,v_y,v_z{)}^{\mathrm{T}}$ is eventually obtained by a coordinate transform, according to Schlüßler et al. (2015). Following Schlüßler et al. (2015), the standard uncertainty of v_x, v_y, and v_z can be calculated by Gaussian uncertainty propagation. The resulting uncertainties read 1.74σ, 1.00σ, and 1.22σ, respectively, assuming an equal uncertainty σ for each of the originally measured (non-Cartesian) velocity components. As a consequence, the uncertainty of all Cartesian velocity components v_x, v_y, and v_z is almost identical in this FM-DGV measurement.

Figure 7 Root mean square (rms) of the output vector fields (l² norm) from Fig. 6 at the lateral position z=0 using all phase values φ regarding the acoustic excitation frequency.

4.2 Results and discussion

The NHHD is applied to the three-dimensional vector field of the measured fluid velocity in order to separate the acoustic particle velocity and the aerodynamic flow velocity. Here, this is only done for the oscillation velocity at the acoustic excitation frequency f_osc, as an example. For this purpose, the time-dependent velocity signal is evaluated regarding the phase φ with respect to f_osc and yields a zero-mean phase-averaged oscillation velocity, like in Haufe et al. (2013). In order to reduce computational errors due to discretization of the spatial derivatives from Eqs. (1)–(7) according to the Eq. (9) and the resulting crosstalk (see Fig. 3), an interpolation of the vector data on a finer grid size (with an interpolation factor N=16) using cubic splines was performed beforehand. As a result, the spatial resolution of initially about 600 µm turns into a grid size of approximately 40 µm. As a result, the crosstalk is decreased, like observed in Sect. 3.2 (although no measurement information is obtained by applying the interpolation).

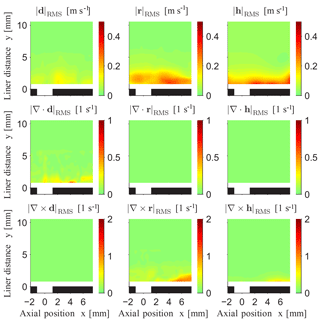
The phase-averaged oscillation velocity vector field, denoted by v in the following, as well as the corresponding divergence and the curl of the vector field, are depicted in Fig. 5, as an example for the plane at z=0. Regarding random deviations, the standard uncertainty of v is about 20 mm s⁻¹ for a measurement duration of 5 s, where a phase resolution of π∕8 is used for phase-averaging (i.e., 500,000 velocity samples are averaged), similar to Haufe et al. (2013). According to Haufe et al. (2014), the phase-averaging acts as a band pass filter, suppressing random velocity terms like the turbulence and measurement noise with a spectral width of 1∕T, where T is the measurement duration. Note that the choice of the phase resolution results from a compromise between short temporal resolution and low velocity uncertainty. In order to further decrease the velocity uncertainty, T may be increased, as proposed by Haufe et al. (2013). According to Fig. 5a, there is a high oscillation velocity in the vicinity of the orifice, which coincides with previous observations by Heuwinkel et al. (2010). The magnitude of the divergence of the oscillation velocity is low compared to its curl; see Fig. 5b and c. Hence, a high vorticity is present, which also agrees well with existing results from Heuwinkel et al. (2010) using a comparable liner (though with circular cross section). There are some domains of high oscillation velocity in Fig. 5a which remain stationary above the orifice and downstream at about x=(2…4) mm. In these places, sources and sinks can be found (see Fig. 5b), which alternate in time. However, most of the domains of high oscillation velocity are convected downstream in time, as do the corresponding domains of high vorticity in Fig. 5c, which agrees with previous results in the identical liner from Schulz et al. (2015).

In order to provide further insight, the NHHD is applied to the measured data following Sect. 2.2. The resulting output vector fields are depicted in Fig. 6, again as an example for the plane at z=0. In the irrotational term d, a structure like a breathing sphere is identified near the orifice at x=2 mm, which coincides with the stationary domains of high oscillation velocity seen in Fig. 5a. In the solenoidal term r there are structures that move downstream, which coincides with the convecting domains of high oscillation velocity from Fig. 5a. In addition, a pulsating structure occurs within the harmonic term h, which could not be determined in Fig. 5, but is discovered using the NHHD. According to the theory of the NHHD, the divergence and curl of v are approximately equivalent to the divergence and the curl of the irrotational term d and the solenoidal term r, respectively. For the final discussion, the root mean square (rms) fields of the values are visualized in Fig. 7 using all phase values regarding the acoustic excitation frequency. According to Figs. 6 and 7, three scientific findings are obtained.

1. The irrotational term d, which is equivalent to the acoustic particle velocity, amounts up to 0.13 m s⁻¹ (rms) in the vicinity of the central orifice at $(x,y)\approx (\mathrm{2}\mathrm{mm},\mathrm{1}\mathrm{mm})$. For comparison, the rms of the acoustic particle velocity of the incident wave would be only about 0.04 m s⁻¹, assuming plane waves and the characteristic impedance of air; see Rossing (2007). Consequently, the local acoustic particle velocity at the orifice is approximately 3 times higher than from the acoustic excitation. Hence, the hypothesis arises that an acoustic source near the facing sheet is supposed to be induced by the interaction of sound and flow. Similar observations have been made, e.g., by Marx et al. (2010) in a liner without bias flow. In contrast, the application of the NHHD in the present paper allows the aerodynamic and the acoustic velocity field to be quantitatively distinguished from each other for the first time.

2. The solenoidal term r, which is associated with the rotational flow field, is mostly higher than d and has a maximum value of 0.31 m s⁻¹ (rms). This proves the generation of flow vortices being induced by the interaction of sound and flow, which agrees well with previous observations, e.g., by Eldredge and Dowling (2003), Rupp et al. (2010), or (with a comparable liner) by Heuwinkel et al. (2010).

3. The harmonic term h, which is associated with the irrotational (and solenoidal) flow field, amounts up to 0.38 m s⁻¹ (rms) and only approximately exhibits the characteristic property $\mathbf{\nabla }\times \mathit{h}=\mathbf{\nabla }\cdot \mathit{h}=\mathrm{0}$ as defined by Eq. (6); i.e., the decomposition is not ideal. Like already investigated in Sect. 3.2, this is caused by the discretization of the vector field data and can be reduced by choosing a smaller grid size. The crosstalk in Fig. 6 according to the Eq. (13) is about −36 and −8 dB regarding divergence and curl, respectively.

To conclude, the application of the NHHD for aeroacoustic analysis is a promising method in order to obtain a better understanding about the interaction of sound and flow in a bias flow liner. The grid size has to be decreased in the future in order to decrease the crosstalk, according to Fig. 3. This can be done by utilizing a finer spatial resolution, e.g., using a velocity profile sensor from Haufe et al. (2014) with micrometer resolution. Alternatively, the interpolation factor can be increased further. Then, the finer discretization will result in smaller computational errors, though the physical information will of course not be enhanced. Note that the computation time using an interpolation factor of N is increased on the order of 𝒪(N⁶) for the complete solution of three-dimensional problems as evident here. As an example, the calculation time for generating the results from Fig. 6, at z=0 only, is about 23 days (for N=16) using a Fujitsu Celsius R920 workstation with an Intel^® Xeon^® hexa-core processor E5-2620 at 2 GHz.

5 Conclusions

The aim of this work is to perform an aeroacoustic analysis of an experimentally obtained volumetric velocity vector field, measured in a bias flow liner. For this purpose, the oscillation velocity with respect to the frequency of the sinusoidal acoustic excitation is evaluated using the natural Helmholtz–Hodge decomposition (NHHD). This vector field decomposition of the fluid velocity into the irrotational acoustic particle velocity and the solenoidal flow velocity is successfully applied on a three-dimensional vector field in a 1 cm³ region of interest. The phase-averaged oscillation velocity is measured at 16³=4096 locations in a generic bias flow liner by Doppler global velocimetry with laser frequency modulation. The application of the NHHD was enabled by the first volumetric measurement in such a liner.

The analysis shows that the flow velocity, which is related to vortices, dominates in the fluid velocity field, which coincides with previous experimental work by Heuwinkel et al. (2010). Moreover, the application of the NHHD also reveals a prominent irrotational flow velocity. In addition, the hypothesis of an aeroacoustic source near the facing sheet of the liner was suggested. Thus, the application of the NHHD offers a promising perspective for the future, especially for the quantitative investigation of the energy transfer from the sound field to the flow field, as proposed in Schulz et al. (2015).

Furthermore, the influence of the grid size on the quality of the NHHD is investigated using synthetic data. As a result, the grid size has to be minimized in order to minimize computational errors. However, this yields a higher computational effort.

In the future, the employment of parallel computing, e.g., using a graphics processing unit, should be considered to save calculation time (see Kirk and Hwu (2010)). On the one hand, this facilitates an in-depth characterization of even more complex vector fields and a detailed uncertainty analysis by statistical means in the future, similar to Ribeiro et al. (2016). On the other hand, an additional calculation of the decomposition of the oscillation velocity regarding overtones of the excitation frequency to study potentially nonlinear damping phenomena is enabled. The analysis of aeroacoustic phenomena contributes to an enhanced understanding of aeroacoustic damping.