Calibration of tri-axial MEMS accelerometers in the low-frequency range – Part 1: comparison among methods

Two alternative experimental procedures for the calibration of tri-axial accelerometers have been compared with traditional methods, performed according the procedures stated in the standard ISO 16063-21. Standard calibration is carried out by comparison with a laser Doppler vibrometer (LDV), used as a primary reference transducer. The main sensitivities have been investigated and, where applicable, also transverse ones. Many aspects have been evaluated: the hypotheses about transverse sensitivities, the simplicity of the procedure, the number of measurements needed, and the effect of typology of transducer, depending on electrical and geometrical contributions. Two different accelerometers have been tested, a piezo-electric accelerometer and a capacitive MEMS accelerometer. A low-frequency range of vibration has been investigated, 3 and 6 Hz, with amplitude of acceleration ranging from 2 to 20 ms⁻². A satisfactory reproducibility of methods has been verified, with percentage differences less than 2.5 %. Anyway, pros and cons of each method are also discussed with reference to their possible use for easy and quick calibration of low-cost tri-axial accelerometers.

1 Introduction

In recent years, there has been a growing interest in micro-electro-mechanical system accelerometers (MEMS), due to their low cost, the possibility of embedding these devices within wireless sensor networks, and the capability of detecting low-amplitude and low-frequency vibrations, operations which are not always feasible with the conventional low-cost sensor boards (Batista et al., 2011; Sabato et al., 2017). It should be considered that MEMS accelerometers, in comparison to high-performance piezo-electric transducers, exhibit lower accuracy in consumer grade applications; however, in the context of extensive applications, such as large sensor networks, in which high accuracy on a wide range of frequency and amplitude is not needed, the technical performances of these accelerometers are considered adequate (Schiavi et al., 2015).

Low-frequency vibration measurements are of great interest in many different fields such as, for instance, energy production (Ripper et al., 2017), structural health monitoring (SHM) of buildings and of civil infrastructures (Sabato et al., 2017; Ranieri et al., 2013), and geotechnical applications (Czech and Gosk, 2017) in the field of human vibration and bio-dynamics (Griffin, 2014), mainly because of the increasing development of MEMS embedded in mobile devices (Halim and Park, 2013) and in applications in the field of the Internet of Things (IoT) (Borgia, 2014).

The evaluation of sensitivities is a key point of the vibration measurements for MEMS accelerometers, and it requires adequate attention from the design phase up to the realization and the use of this kind of sensor.

In this paper, new calibration techniques are investigated, with the purpose of increasing the flexibility of the traditional calibration procedures (ISO 16063-1, 1998; ISO 16063-11, 1999; ISO 16063-31, 2009), to tailor them to the variable conditions and requirements of the field while guaranteeing, at the same time, traceability and accuracy (Schiavi et al., 2015; D'Emilia et al., 2011, 2015). An example is the possibility of developing procedures that could be implemented both on-line and in-line (Frosio et al., 2009, 2012; Glueck et al., 2012; Fong et al., 2008).

On-line calibration refers to the possibility of calibrating during assembly in industrial processes, for continuous monitoring and controlling of processes. In-line calibration refers to the calibration of sensors installed on an industrial plant, directly carried out on the production line to be monitored without moving it to a laboratory.

The possibility of calibrating sensors in the field is an interesting issue not only for practical and economic reasons, but also from a technical point of view. In fact, the MEMS sensor output depends on temperature and, in general, on other environmental conditions (Wu et al., 2002). Therefore, these accelerometers have to be calibrated in the field when a realistic assessment of the measurement uncertainty is an important requirement (Frosio et al., 2009, 2012; Glueck et al., 2012; Fong et al., 2008).

The research for new methods for the on-line and in-line calibration of MEMS is confirmed as one of the points of main relevance. In fact, some procedures are proposed based on different algorithms. In Chen and Han (2011) the wavelet neural network is used for optimizing and compensating for the variation of the MEMS acceleration sensors due to temperature change. Rohac et al. (2015) propose a method for calibration of MEMS tri-axial inertial sensors, using a gravity-based calibration method under static conditions. Geist et al. (2017) propose a methodology based on the linearization, used for the reduction of the measurement error of the device. The optimization algorithm is validated on an experimental set-up, considering the accelerometer in static state, and rotating it randomly in 30 different orientations. These methods are static-based methods and do not consider aspects arising from the experimental practice (e.g. the dynamic behaviour of the phenomena analysed).

In summary, the following main requirements for testing and calibration of accelerometers for the above-mentioned applications should be met:

• to lower the cost of calibration and testing (low-cost calibration);

• to enhance the sensors' operability, also in dynamic conditions, similar to those of their actual use (dynamic conditions);

• to guarantee the traceability of the methodology, up to the primary calibration (traceability);

• to streamline the production process and to reduce loss in times and costs of possible deviations from the validated information, also in the case of on-line and in-line calibration (on-line and in-line calibration);

• to avoid complex models and algorithms, in order to be easily transferred onto the field, thus increasing their operability (simplicity and operability).

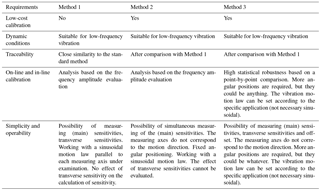
A quantitative comparison among three methods is carried out. Two methods have been selected that are potentially able to fulfil the above-mentioned requirements, in a different way, with respect to the standard method, used as a reference. The standard method, Method 1, is performed according to the procedures stated in the ISO Standard 16063 series (ISO 16063-1, 1998; ISO 16063-11, 1999; ISO 16063-21, 2003; ISO 16063-31, 2009), to support the traceability. The second one, Method 2 (Schiavi et al., 2015), allows us to determine the three main sensitivities, simultaneously. The last one (Method 3; D'Emilia et al. ,2015, 2016a, b) gives the possibility of obtaining the main sensitivities, transverse sensitivities and offset terms.

In Sect. 2, the methods are described and a discussion of the way each method fits the above requirements is carried out. In Sect. 3, the test bench used for the experimental set-up, together with the typology of the accelerometers that have been used, and the planned tests are outlined. The indicators used for the comparison purposes are also identified. In Sect. 4 the results for the two typologies of sensors analysed are presented and discussed. Conclusions and hints for future works end the paper.

2 Calibration methods

In the following sections, the methods of calibration and the parameters considered for the comparison will be shown. Then, the test bench used for the experimental tests will also be described.

2.1 Method 1: the standard ISO 16063 series

The standard (ISO 16063-1, 1998) defines the sensitivity for a linear transducer as the ratio of the input during sinusoidal excitation, parallel to a specified axis of sensitivity at the mounting surface.

The procedure to be used for primary calibration of rectilinear accelerometers to obtain magnitude and phase lag of the complex sensitivity by steady-state sinusoidal vibration and laser interferometry is described in ISO 16063-11 (1999). The sinusoidal motion applied by the vibration generator is along a well-defined straight line, with negligible lateral motions.

In this paper, the traceability to primary national standards through a secondary standard is accomplished by applying the specifications in ISO 16063-21 (2003). Additionally, the standard (ISO 16063-31, 2009) defines the transverse sensitivity of an accelerometer, S_T, as the sensitivity to acceleration applied at right angles to its geometric axis. S_T, corresponding to a specific test direction, is calculated as (1), where ${\widehat{V}}_{\mathrm{out}}$ is the amplitude of the output signal of the transducer and ${\widehat{a}}_{\mathrm{T}}$ is the amplitude of the acceleration in the test direction. The test direction is perpendicular to the axis of sensitivity.

$$\begin{array}{}\text{(1)}& S_{\mathrm{T}}={\displaystyle \frac{{\widehat{V}}_{\mathrm{out}}}{{\widehat{a}}_{\mathrm{T}}}}\end{array}$$

The standard ISO 16063-31 (2009) deals with uni-axial accelerometers, excited along directions perpendicular to their sensitive axes.

Extending the indications of the standard to the case of a tri-axial accelerometer, each axis of the sensor could be tested by applying a known acceleration to another axis, with the purpose of calculating according to Eq. (1) the transverse sensitivity of the first axis when excited along the direction of the second one.

Then, by exciting each single axis of a sensor, it is possible to calculate six transverse sensitivities, which express the effect of the acceleration along a single axis, with respect to the other ones.

These transverse sensitivities will be indicated as S_xy, S_xz, S_yx, S_yz, S_zx, and S_zy, where the first subscript indicates the axis with reference to which the sensitivity is calculated, and the second one indicates the direction of the excitation.

A similar approach is applied for the determination of the magnitude of the acceleration sensitivities (S_xx, S_yy, S_zz). The phase lag is assumed to be negligible.

As an example, when the vibration is according to the x axis, the sensitivity is calculated as Eq. (2), while the transverse sensitivities S_yx and S_zx can be evaluated as Eqs. (3) and (4), where V_x, V_y and V_z are the amplitudes of the x, y and z outputs of the accelerometer under test, and a_x is the amplitude of the reference signal in the x direction.

$$\begin{array}{}\text{(2)}& {\displaystyle }& {\displaystyle }{S}_{xx}={\displaystyle \frac{V_x}{a_x}}\text{(3)}& {\displaystyle }& {\displaystyle }{S}_{yx}={\displaystyle \frac{V_y}{a_x}}\text{(4)}& {\displaystyle }& {\displaystyle }{S}_{zx}={\displaystyle \frac{V_z}{a_x}}\end{array}$$

The same procedure is used for the other sensitivities, when the vibration is along the y axis (S_yy, S_xy, S_zy) and z axis (S_zz, S_xz, S_yz), respectively.

2.2 Method 2

Method 2 involves the simultaneous excitation of the three axes of the accelerometer under test.

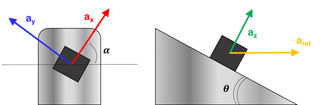
For this purpose, the accelerometer has to be mounted onto the surface of a clamp, inclined at an angle θ=35^∘ with respect to the horizontal plane (Fig. 1) on which the motion is realized; furthermore, the accelerometer has to be rotated on the clamp surface with an angle α=45^∘, in order to simultaneously excite the three axes in the same way, with a single horizontal sinusoidal acceleration (Fig. 1) (Schiavi et al., 2015).

In this way, accelerations of similar amplitude are realized along the three axes, which can be simultaneously calibrated.

The reference accelerations along the three axes can be obtained as follows in Eqs. (5), (6) and (7):

$$\begin{array}{}\text{(5)}& {\displaystyle }& {\displaystyle }{a}_x=-a_{\mathrm{ref}}\cdot \cos \left(\mathit{\theta }\right)\cdot \sin \left(\mathit{\alpha }\right),\text{(6)}& {\displaystyle }& {\displaystyle }{a}_y=-a_{\mathrm{ref}}\cdot \cos \left(\mathit{\theta }\right)\cdot \cos \left(\mathit{\alpha }\right),\text{(7)}& {\displaystyle }& {\displaystyle }{\mathrm{a}}_{\mathrm{z}}=a_{\mathrm{ref}}\cdot \sin \left(\mathit{\theta }\right),\end{array}$$

where a_ref is the acceleration in the motion direction, measured by a reference sensor.

Figure 1 Inclined clamp – scheme.

The output signal and the reference one are analysed by the fast Fourier transform in correspondence to the oscillation frequency, with the purpose of evaluating their spectral amplitudes. The constant terms, gravity-dependent, do not affect the results.

S_xx is evaluated according to Eq. (2), where V_x is the spectral amplitude of the output signal of the x axis of the accelerometer under test, and a_x is the spectral amplitude of the reference signal in the same direction.

The same approach allows us to evaluate S_yy and S_zz, respectively, when the other measuring axes of the accelerometer are considered.

This approach does not allow us to calculate the transverse sensitivities, since similar acceleration components are realized along all axes, simultaneously, without the possibility of extracting the effect of transverse sensitivities. A periodic verification that the transverse sensitivities are negligible (< 5 % with respect to the main sensitivities) is necessary for the typology of sensor considered, according to Method 1, described in Sect. 2.1.

Table 1 Pros and cons of the methods with respect to requirements.

2.3 Method 3

This method is based on the following model, describing the relation between the input accelerations and the output signals (Eq. 8), where V = (V_i) is the output array, A = (a_i) is the reference accelerations array, S = (S_ij) is the sensitivity matrix and Q = (q_i) represents the offset array.

$$\begin{array}{}\text{(8)}& \left(\begin{array}{l}{V}_x\\ V_y\\ V_z\end{array}\right)=\left(\begin{array}{lll}{S}_{xx}& S_{xy}& S_{xz}\\ S_{yx}& S_{yy}& S_{yz}\\ S_{zx}& S_{zy}& S_{zz}\end{array}\right)\cdot \left(\begin{array}{l}{a}_x\\ a_y\\ a_z\end{array}\right)+\left(\begin{array}{l}{q}_x\\ q_y\\ q_z\end{array}\right)\end{array}$$

Then, a total of 12 parameters (main sensitivities, transverse sensitivities and offsets) are evaluated; a linear least squares optimization is used to estimate them, as described in the references (D'Emilia et al., 2015, 2016a, b).

To avoid dependence among the input data for the least squares optimization, the sensor has to be positioned in different angular positions with respect to the motion direction. The sensor should be mounted with an angle θ with respect to the horizontal plane on which the motion is carried out, repeating measurements for different angles α (Fig. 1). In Method 3, angle θ could be anything. In this comparison, it will be set the same as Method 2 (θ = 35^∘).

The method requires a minimum number of four different input acceleration vectors, although more measurements may give a more robust calibration. The inputs correspond to different values for time and angles α.

The reference accelerations along the three axes can be obtained from Eqs. (9), (10), and (11), where g is the gravity acceleration, and a_ref(t) is the time-varying acceleration in the motion direction and measured by a reference sensor.

$$\begin{array}{}\text{(9)}& {\displaystyle }& {\displaystyle }{a}_x\left(t\right)=-a_{\mathrm{ref}}\left(t\right)\sin \left(\mathit{\alpha }\right)\cos \left(\mathit{\theta }\right)-g\cdot \sin \left(\mathit{\theta }\right)\cdot \sin \left(\mathit{\alpha }\right)\text{(10)}& {\displaystyle }& {\displaystyle }{a}_{\mathrm{y}}\left(t\right)=-a_{\mathrm{ref}}\left(t\right)\cdot \cos \left(\mathit{\alpha }\right)\cdot \cos \left(\mathit{\theta }\right)-g\cdot \sin \left(\mathit{\theta }\right)\cdot \cos \left(\mathit{\alpha }\right)\text{(11)}& {\displaystyle }& {\displaystyle }{a}_z\left(t\right)=a_{\mathrm{ref}}\left(t\right)\cdot \sin \left(\mathit{\theta }\right)-g\cdot \cos \left(\mathit{\theta }\right)\end{array}$$

It must be pointed out that the constant terms in formulas (12–14), due to the components of the gravity acceleration, should not be considered for sensors, like piezo-electric ones, that are not sensitive to constant accelerations.

Figure 2 Time behaviour of accelerometer outputs and reference inputs: example.

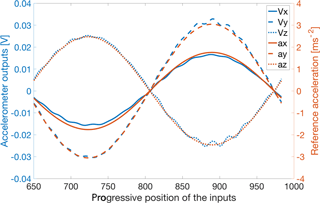
In Fig. 2, as an example, the time behaviour of both the accelerometer outputs (V_x, V_y, V_z) and the reference signals (a_x, a_y, a_z) is shown, in the time domain (α=30^∘, sampling frequency 1000 Hz, excitation frequency f₁=3 Hz, and number of inputs = 333, corresponding to one period of oscillation).

2.4 Discussion of the methods

Table 1 summarizes some considerations concerning the specific characteristics of the methods to be compared, in order to give information about the possibility of using them in-field, for the on-line and in-line calibration of MEMS, and about their capability of satisfying requirements involved in these applications.

2.5 Test bench and test procedure

For the comparison among calibration methods, two different accelerometers have been considered:

• a MEMS accelerometer (Sequoia FastTracer^®) with a capacitive transduction system, with digital output to a computer, via a standard USB port. The output indicates the acceleration (nominal sensitivity of the order of 1, dimensionless);

• a piezo-electric accelerometer (PCB 356A15) with analogue output (nominal sensitivity of the order of 10 mV m⁻¹ s²).

The test bench used is a vibrating table with a horizontal linear slide, the APS 113 ELECTRO-SEIS shaker (Fig. 3). It is a long-stroke, electro-dynamic force generator specifically suitable for low-frequency vibration testing. The slide is moved according to a sinusoidal law.

Figure 3 APS 113 ELECTRO-SEIS horizontal vibrating table.

In Method 1 the accelerometer is fixed directly on the horizontal vibrating table, with one of the three axes parallel to the motion direction. All three axes are tested in this way, recursively.

In Method 2 and Method 3 an inclined steel clamp is fixed on the vibrating table; the inclination angle θ is 35^∘ with respect to the horizontal plane (Fig. 4). The inclined steel clamp allows us to obtain a specified angle α (Method 2) or different angles α (Method 3). The motion of the vibrating table is accurately monitored by a laser Doppler vibrometer (LDV), as depicted in Fig. 4c.

Figure 4 Particulars of the test bench: indication of the directions of acceleration. Piezo-electric (a) and MEMS (b) sensors, mounted on the inclined clamp. Laser vibrometer (c).

The amplitude of the reference acceleration signal is obtained by applying Eq. (12), ω being the pulsation of the sinusoidal motion and v_vib the velocity measured by the LDV.

$$\begin{array}{}\text{(12)}& a_{\mathrm{ref}}=\mathit{\omega }\cdot v_{\mathrm{vib}}\end{array}$$

The data acquisition system (DAQ) used is the NI USB-4431 by National Instruments. The module consists of a single analogue output and four analogue input channels for reading (one is connected to the LDV and the other three to the outputs of the PCB accelerometer under test); each channel is equipped with antialiasing filters. The output channel drives the vibrating table. LabVIEW software is used for DAQ signal acquisition.

Table 2 Parameters used for the comparison.

2.6 Description of the experiments

Tests are carried out at the excitation frequencies of f₁=3 Hz and f₂=6 Hz, at different amplitudes in the range 2 to 20 ms⁻². Independent tests are carried out in two different configurations.

• Method 1: parallel excitation, with respect to the measuring axes of the accelerometer. The sensors are excited along the main measuring components x, y and z axes, according to standards (ISO 16063-1, 1998; ISO 16063-11, 1999; ISO 16063-31, 2009).

• Method 2: inclined excitation with respect to the measuring axes of the accelerometer (θ = 35^∘, α = 135^∘).

• Method 3: inclined excitation, with respect to the measuring axes of the accelerometer. Each sensor is rotated, according to four different angles, α, between the x axis of the accelerometer and the horizontal. Depending on the specific sensor under test, α takes the following values: 0, 30, 90, 120, 135, and 210^∘, as in Fig. 5.

2.7 Comparison between post-processing techniques

In order to determine whether and to what extent the calibration methodologies are equivalent, the following results are compared, obtained through the application of the three above-mentioned methodologies:

• calibration tests of the same accelerometer, on the same test bench (high-performance linear slide);

• calibration tests of different accelerometers, of different technology and quality levels.

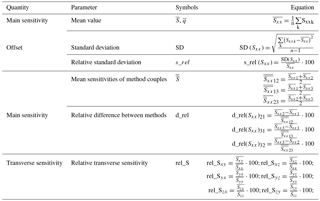
The comparison of the results and the assessment of the possible equivalence between methods is made by the parameters whose symbols are defined in Table 2, where M and N assume the following numbers: 1, 2, 3, depending on the specific method applied (e.g. $\mathrm{d}\mathrm{\_}\mathrm{rel}{\left(S_{xx}\right)}_{MN}$, for M = 3 and N = 2 stands for $\mathrm{d}\mathrm{\_}\mathrm{rel}{\left(S_{xx}\right)}_{\mathrm{32}}$, i.e. the relative difference between Method 3 and Method 2).

Details on the evaluation of each parameter are reported in Appendix A, taking as an example the main sensitivity S_xx (i.e. the main sensitivity along the measuring x axis of the accelerometer).

In the following, the quantities used for comparison are summarized:

• the sensitivities and transverse sensitivities of each accelerometer and the related variability;

• the relative differences between methods of the main and the transverse sensitivities;

• sensitivities obtained by applying each method, taking into account the specific uncertainty.

3 Results

This section is organized as follows: Sects. 4.1 and 4.2 report the results obtained for the two accelerometers under test (piezo-electric and MEMS), respectively. In each of them, the results of the three methods described are shown and a comparison among them is carried out.

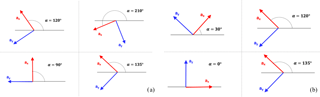
Figure 5 Angles of rotation of the accelerometers: (a) MEMS accelerometer; (b) piezo-electric accelerometer.

Figure 6 3-D diagram for the sensitivity matrix: scheme and notation.

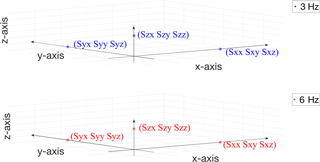
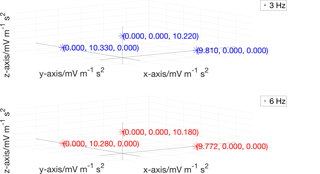
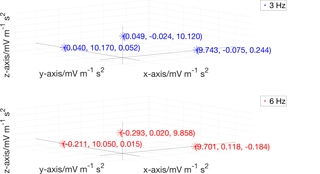
For the results obtained for the sensitivity matrix, a graphical representation in the 3-D space is used according to the scheme of Fig. 6. Each point represents a row of the sensitivity matrix. The sensitivity components are expressed in millivolt per metre second squared (mV m⁻¹ s²), for the piezo-electric accelerometer, while they are dimensionless for the MEMS accelerometer, since the digital output values are directly expressed in metres per second squared (m s⁻²).

The x axis represents the locus of the ideal response along the x axis itself of the three-axis accelerometer (S_xx≠0; S_xy = 0; S_xz = 0), meaning negligible transverse sensitivities. The same applies to the y axis and z axis.

Table 3 Piezo-electric accelerometer: comparison between methods (%).

Table 4 MEMS accelerometer: comparison between methods (%).

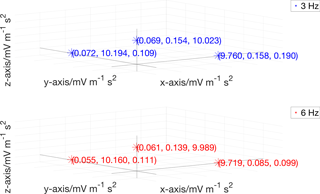
Figure 7 Piezo-electric accelerometer: sensitivity matrix obtained by means of Method 1 (3-D diagram).

3.1 Piezo-electric accelerometer

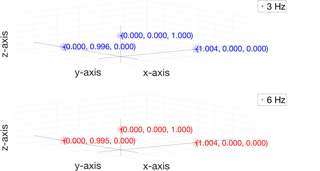
3.1.1 Method 1

Figure 7 represents the sensitivity matrix obtained by applying Method 1, as described in Sect. 2.1, at 3 Hz (upper side) and 6 Hz (bottom side). The relative standard deviation (s_rel), defined in Table 1 and Appendix A, of all main sensitivities is negligible, being less than 0.03 %.

Figure 8 Piezo-electric accelerometer: sensitivity matrix obtained by means of Method 2 (3-D diagram).

3.1.2 Method 2

Figure 8 represents the sensitivity matrix obtained by applying Method 2, as described in Sect. 2.2, at 3 Hz (upper side) and 6 Hz (bottom side). The relative standard deviation (s_rel) of all main sensitivities is negligible, being less than 0.04 %.

Figure 9 Piezo-electric accelerometer: sensitivity matrix obtained by means of Method 3 (3-D diagram).

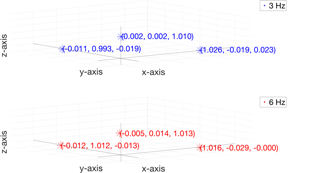
3.1.3 Method 3

Figure 9 represents the sensitivity matrix obtained by applying Method 3, as described in Sect. 2.3, at 3 Hz (upper side) and 6 Hz (bottom side). The relative standard deviation (s_rel) of all main sensitivities is negligible (less than 0.08 %). As a first approximation, the mean main sensitivities appear coherent to those obtained through Method 1 (Fig. 7). The offset vectors at f₁=3 Hz and f₂=6 Hz are as in the following, and they are considered negligible; therefore, their variability is meaningless. For the piezo-electric accelerometer under investigation, the output values are in millivolt (mV), and as a consequence the offset values are expressed in terms of voltage.

$${\left(\begin{array}{l}{q}_{\mathrm{x}}\\ q_{\mathrm{y}}\\ q_{\mathrm{z}}\end{array}\right)}_{f\mathrm{1}}=\left(\begin{array}{l}\mathrm{0.3113}\mathrm{mV}\\ \mathrm{0.5427}\mathrm{mV}\\ \mathrm{0.06098}\mathrm{mV}\end{array}\right);$$

$${\left(\begin{array}{l}{q}_x\\ q_y\\ q_z\end{array}\right)}_{f\mathrm{2}}=\left(\begin{array}{l}\mathrm{0.2477}\mathrm{mV}\\ \mathrm{0.5668}\mathrm{mV}\\ \mathrm{0.5839}\mathrm{mV}\end{array}\right).$$

3.1.4 Comparison between methods

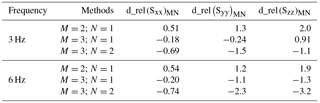
Relative differences between methods (d_rel) obtained by applying the three methods are reported in Table 3, when the piezo-electric sensor is excited at 3 and 6 Hz, respectively.

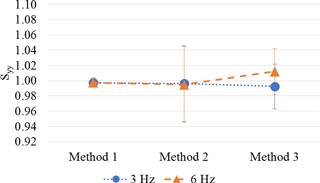
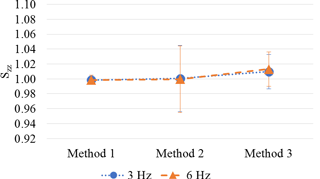
Differences between Method 2 and Method 1 are always positive up to 2 %. Differences between Method 3 and Method 1 are both negative and positive and in the range ±1.3 %. The highest differences arise between Method 3 and Method 2, being $\mathrm{d}\mathrm{\_}\mathrm{rel}{\left(S_{zz}\right)}_{\mathrm{32}}=-\mathrm{3.2}$ % (at 6 Hz).

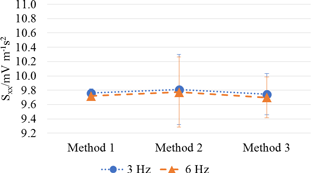
Figure 10 Piezo-electric accelerometer: comparison between methods (main sensitivity along the x axis, S_xx).

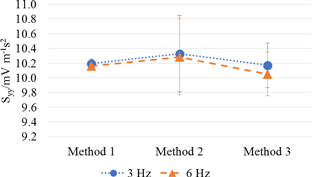
Figure 11 Piezo-electric accelerometer: comparison between methods (main sensitivity along the y axis, S_yy).

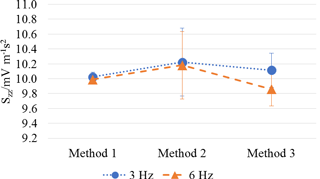
Figure 12 Piezo-electric accelerometer: comparison between methods (main sensitivity along the x axis, S_zz).

Figures 10–12 highlight, for each axis, the relative position and differences among methods. Expanded uncertainty (k = 2) of results, estimated according to D'Emilia et al. (2018), is also represented in Figs. 10–12 by error bars.

3.1.5 Reproducibility: transverse sensitivities

The relative transverse sensitivities (rel_S) for all axes, as defined in Table 1 and Appendix A, are all under 3 %. These have been obtained by means of Method 1 and Method 3, which take these terms into account explicitly, and can be considered negligible in both cases.

Figure 13 MEMS accelerometer: sensitivity matrix obtained by means of Method 1 (3-D diagram).

3.2 MEMS accelerometer

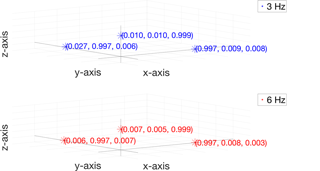
3.2.1 Method 1

Figure 13 represents the sensitivity matrix obtained by applying Method 1, as described in Sect. 2.1, at 3 Hz (upper side) and 6 Hz (bottom side). The relative standard deviation (s_rel), defined in Table 1 and Appendix A, of all main sensitivities is negligible (less than 0.02 %).

Figure 14 MEMS accelerometer: sensitivity matrix obtained by means of Method 2 (3-D diagram).

3.2.2 Method 2

Figure 14 represents the sensitivity matrix obtained by applying Method 2, as described in Sect. 2.2, at 3 Hz (upper side) and 6 Hz (bottom side). Also in this case, the relative standard deviation (s_rel) appears negligible with respect to the mean sensitivities, which results in less than 0.09 %.

Figure 15 MEMS accelerometer: sensitivity matrix obtained by means of Method 3 (3-D diagram).

3.2.3 Method 3

Figure 15 represents the sensitivity matrix obtained by applying Method 3, as described in Sect. 2.3, at 3 Hz (upper side) and 6 Hz (bottom side). The relative standard deviation (s_rel) of all main sensitivities is negligible (less than 0.06 %). The offset vectors at f₁=3 Hz and f₂=6 Hz are as in the following.

q_x values are not negligible at both frequencies. For the MEMS accelerometer under investigation, the digital output values are in metres per second squared (m s⁻²), and as a consequence the offset values are expressed in terms of acceleration.

$${\left(\begin{array}{l}{q}_x\\ q_y\\ q_z\end{array}\right)}_{f\mathrm{1}}=\left(\begin{array}{l}\mathrm{0.3576}{\mathrm{ms}}^{-\mathrm{2}}\\ -\mathrm{0.06304}{\mathrm{ms}}^{-\mathrm{2}}\\ \mathrm{0.1650}{\mathrm{ms}}^{-\mathrm{2}}\end{array}\right);$$

$${\left(\begin{array}{l}{q}_x\\ q_y\\ q_z\end{array}\right)}_{f\mathrm{2}}=\left(\begin{array}{l}\mathrm{0.1662}{\mathrm{ms}}^{-\mathrm{2}}\\ -\mathrm{0.07268}{\mathrm{ms}}^{-\mathrm{2}}\\ \mathrm{0.1345}{\mathrm{ms}}^{-\mathrm{2}}\end{array}\right).$$

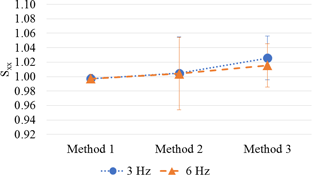
3.2.4 Comparison between methods

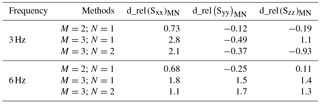
The relative differences between methods (d_rel) obtained by applying the three methods are reported in Table 4, when the MEMS sensor is excited at 3 and 6 Hz. Figures 16–18 highlight the differences between methods in terms of the mean main sensitivities obtained.

Figure 16 MEMS accelerometer: comparison between methods (main sensitivity along the x axis, S_xx).

Figure 17 MEMS accelerometer: comparison between methods (main sensitivity along the y axis, S_yy).

Figure 18 MEMS accelerometer: comparison between methods (main sensitivity along the x axis, S_zz).

Expanded uncertainties (k = 2) of results, estimated according to D'Emilia et al. (2018), are also represented in Figs. 16–18 by error bars.

The differences of Method 3 with respect to Method 1 are higher than those of Method 2.

3.2.5 Reproducibility: transverse sensitivities

The relative transverse sensitivities (rel_S) for all axes obtained by means of Methods 1 and 3, which take these terms into account explicitly, are all under 4 %, and can be considered negligible in both cases.

3.3 Discussion of the results

The highest differences of main sensitivity values between the indications of Method 1 and Method 3, of the order of 2 %, are associated with higher values of main sensitivity and offset uncertainty, as evaluated in Method 3. The ability to calculate together transverse sensitivities and Q = (q_i) terms is a valuable capability, even though some interactions between them could appear, especially when static acceleration can be measured as in a MEMS accelerometer. No significant differences arise in the case of a piezo-electric accelerometer.

The main results are according to the following items:

• the methods offer reproducible results if differences between them and the uncertainty of each method are taken into account;

• the uncertainty of Method 1, very close to the standard procedure, is very low, of the order of 0.5 %. Anyway, if the calibration procedure is considered, it is more complex and expensive than the other ones; furthermore, it seems not suitable for in-field application, with many of the procedure steps similar to a primary calibration;

• Method 2 is the quickest and simplest method among the ones that have been considered, and it is suitable for in-field applications. It does not allow us to evaluate the transversal sensitivities and their effect. This aspect strongly affects its uncertainty: if all the uncertainty contributions are considered, its relative uncertainty is of the order of 5 %. It is unsuitable for applications where transversal sensitivity effects could be relevant.

• The uncertainty of Method 3 is of the order of 3 %, that is, an intermediate behaviour, as for precision. It is intended to be capable of fitting in a satisfactory way most requirements for in-line and on-line calibration. This method allows the evaluation of transversal sensitivity and of offset terms; therefore, if these effects are remarkable, they can be estimated and do not affect the precision of the calibration.

4 Conclusions

The reproducibility of different methods for calibration of tri-axial accelerometers has been evaluated by means of a high-performance test bench, based on a linear slide and a high-accuracy laser Doppler vibrometer as a reference. The main sensitivities have been analysed and, where applicable, also transversal ones, in order to get information about the possibility of using new methods for the on-line and in-line calibration of MEMS and about the capability of the methods of satisfying requirements involved in these applications, like low-cost calibration, operability, traceability and simplicity of procedures.

Two different accelerometers have been tested, a piezo-electric one and a MEMS one of capacitive type, different with reference to the ability to measure a constant acceleration.

The comparison refers to the following calibration procedures:

• Method 1, extending the indications of the standard to the case of a tri-axial accelerometer;

• Method 2, involving the simultaneous excitation of all three axes of the accelerometer under test, mounting it onto the surface of a clamp;

• Method 3, describing the relation between the input accelerations and the output signals in terms of the sensitivity matrix S=(S_ij) and the offset vector Q=(q_i).

A low-frequency range of vibration has been studied, 3 to 6 Hz, with amplitude of acceleration ranging from 2 to 20 ms⁻², operated along one axis.

The methods offer reproducible results if differences between them and the uncertainty of each method are taken into account, for both piezo-electric and MEMS accelerometers. Differences and extended uncertainty are of the order of a few percent.

Methods 2 and 3 appear suitable for in-field applications, even though some differences arise, in particular the following.

• Method 2 is quick and simple. Anyway, it does not allow us to evaluate the transversal sensitivities and their effect. This aspect strongly affects its uncertainty: if all the uncertainty contributions are considered, its relative uncertainty is of the order of 5 %. It is unsuitable for applications where transversal sensitivity effects could be relevant.

• The uncertainty of Method 3 is of the order of 3 %, that is, generally satisfactory, as for precision. This method allows the evaluation of transversal sensitivity and of offset terms; therefore, if these effects are remarkable, they can be estimated and do not affect the precision of the calibration. It is able to fit in a satisfactory way most requirements for in-line and on-line calibration and to compensate in a satisfactory manner most of the uncertainty causes in the calibration of tri-axial accelerometers.

Appendix A: Parameters used for the comparison

In the following, the parameters of Table A1 have been made more explicit. The equations referring to S_xx are also applied to the main sensitivities S_yy and S_zz and to the offset vector, q_x, q_y, q_z (when Method 3 is taken into account).

It has to be pointed out that the variability of the results is evaluated on six entire cycles of oscillation (n=6 and the subscript k denotes the kth cycle). For each accelerometer, for each kind of test, three repetitions are executed, in repeatability conditions.

Table A1 Parameters used for the comparison: symbols and equations.