Comparison of defect detection limits in Lorentz force eddy current testing and classical eddy current testing

Lorentz force eddy current testing (LET) is a motion-induced eddy current testing method in the framework of nondestructive testing. In this study, we address the question of how this method is classified in comparison with a commercial eddy current testing (ECT) measurement device ELOTEST N300 in combination with the probe PKA48 from Rohmann GmbH. Therefore, measurements using both methods are performed and evaluated. Based on the measurement results, the corresponding defect detection limits, i.e., up to which depth the defect can be detected, are determined and discussed. For that reason, the excitation frequency spectrum of the induced eddy currents in the case of LET is considered.

1 Introduction

Classical eddy current testing (ECT) methods are based on a time-changing magnetic field that induces eddy currents in the electrically conducting specimen under study. Common ECT uses an alternating-current-driven coil, which produces an alternating magnetic field that generates eddy currents in the specimen. In contrast, motion-induced eddy current testing (MECT) methods are based on the relative motion between a stationary magnetic field source and the specimen under study that generates eddy currents. In recent years different MECT methods have been developed. Ramos et al. (2013) carried out an investigation using a DC coil as a stationary magnetic field source instead of a permanent magnet (PM) (Ramos et al., 2013). The perturbation of the magnetic field caused by a defect was measured by giant magnetoresistance (GMR) sensors. Extending this line of research, GMR sensors were replaced by single or differential pick-up coils (Ramos et al., 2014).

The basic principle of Lorentz force eddy current testing (LET) was introduced in 2008 by Brauer and Ziolkowski (2008) and is shown in Fig. 1a. It is based on the relative translational motion between a PM and the specimen under study. Due to this relative motion, eddy currents are induced, leading to a Lorentz force acting on the conductor and, according to Newton's third law, on the PM. In the presence of a defect, the eddy currents are perturbed as well as the Lorentz force. Therefore, LET can be described as a MECT method. In contrast to ECT and other MECT methods, the force is measured to identify the defect. Experimental and numerical studies on LET were carried out by Uhlig (2013) and Zec (2013). Recent investigations have focused on dimensional analysis and similarity solutions (Carlstedt, 2017) and optimal sensor design and uncertainty analysis, broadening the understanding of LET (Weise, 2016). Using a consolidated experimental setup, the question as to how the detection depth in nondestructive material evaluation compares to ECT is addressed in this paper. Therefore, we extend the comparison of ECT and LET done by Carlstedt et al., focusing in this study on the detection limit of LET and ECT for deep-lying defects in solid specimens (Carlstedt et al., 2013).

2 Methods

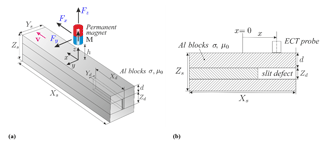
Figure 1a illustrates the basic principle of LET. The specimen under study passes by the permanent magnet with a constant velocity v. Due to the relative motion, eddy currents are induced in the specimen. This leads to a Lorentz force acting on both the conductor and the PM. In the case of a defect in the specimen, the eddy currents and the Lorentz force are perturbed. By measuring the force acting on the PM, this force perturbation enables defect detection, localization, and reconstruction (Brauer et al., 2014). For a low product of velocity and conductivity as used here, the drag force is proportional to the product of velocity and conductivity (Carlstedt et al., 2016). This relationship can be used to adopt the measuring parameters to the current application.

In order to determine the detection limit of LET and ECT, we use a specimen with a long slit of defined geometry, which is inspired by a study of Mook (Mook et al., 2006). Because of limiting manufacturing possibilities, it is not possible to produce a solid specimen with a defined internal defect. For this reason the specimen is split up into three separate aluminum blocks made of the aluminum alloy (EN AW-5754). The size of the specimen is X_S=250 mm, Y_S=50 mm, and Z_S=70 mm. One of these blocks has got a pseudo-infinite defect of length X_d=100 mm, Y_d=2 mm, and Z_d=20 mm (see Fig. 1). Solid blocks of different heights are combined, enabling different defect depths d at a constant total specimen height Z_S.

Figure 2 Measurement setups for LET (a) and ECT (b).

Common eddy current testing uses an alternating-current-driven coil to generate an alternating magnetic field. The eddy currents generate a secondary magnetic field which can be detected by a secondary coil. Usually, the change of the impedance of the secondary coil is used to evaluate the material under study. The change of impedance due to the presence of a defect on or near the surface of the specimen can be detected (García-Martín et al., 2011; Hellier, 2003). Figure 1b shows the ECT measurement principle which was employed in this study.

3 Experimental setups and measurement procedures for LET and ECT measurements

3.1 LET measurement setup

The LET measurements are performed with the BASALT-C MMP-15 (TETRA GmbH, 2015) (see Fig. 2a). This measurement device consists of the mechanical system and the control cabinet. In order to reduce external influences on the force sensing unit, the mechanical system is set on a granite block with high mass to increase the inertia. A linear direct drive is mounted on the granite block to realize the movement in the x direction of the investigated specimen. This direct drive enables accelerations up to 50 m s⁻² and maintains a constant velocity with a negligible standard deviation of 2.19 × 10⁻¹⁰ mm s⁻¹. A granite portal is installed which spans over the linear drive. On this portal, spindle drives in the z and y direction are mounted, to position different sensor types above the specimen fixed to the slide of the linear drive. All drives and the data acquisition are controlled via the panel PC in the control cabinet. The integration of the acquisition task and the positioning task allows complex measurement series to be programmed in G-code (TETRA GmbH, 2015).

3.2 LET measurement procedure

For the LET experiments, the stacked aluminum blocks are mounted on the x drive. The permanent magnet is positioned centered in the y direction above the specimen (and hence centered in the y direction above the slit). The z coordinate is set by moving the PM down until the desired gap to the specimen (lift-off distance h) is adjusted. At the beginning of the measurement, the x drive accelerates the specimen from a start position outside the magnetic field of the PM up to the desired velocity v. At the same time the PC acquires the signal from the force sensors and positional data from the drives simultaneously with a sampling frequency f_s=1000 Hz. After passing the magnetic field of the PM, the x drive as well as the acquisition is stopped and the specimen is moved back to the starting position. Now, the scan can be repeated. In this experiment, the strain gauge force sensor K3D40 from ME-Meßsysteme GmbH (2014) is used. The nominal force of this triaxial sensor is ±2 N in all three directions. The upper side of the force sensor is mounted at the positioning portal above the linear drive in the x direction. At the bottom side, the mount which carries the PM is fixed. Due to the fact that stacked aluminum blocks are used as a specimen instead of a solid body, we swapped the block with the long slit with a block of the same aluminum alloy and the same geometry but without a slit to compare the measurement with and without a defect.

3.3 ECT measurement setup

In order to perform the ECT measurement, the ECT device ELOTEST N300 in combination with the probe PKA48 from Rohmann GmbH (2003) is used. The probe is a differential ECT probe and includes secondary pick-up coils. The structure of the probe was already investigated in detail by Porzig et al. (2014). This probe is best suited from the available probes to detect deep-lying defects. For obtaining appropriate measurements, a stand-alone chuck apparatus is designed which allows the ECT probe to be positioned at specified positions in the x direction on the surface of the specimen (stacked aluminum blocks) as seen in Figs. 1b and 2b. A guide at the apparatus ensures that the ECT probe is positioned centered in the y direction to the specimen (and hence to the slit).

3.4 ECT measurement procedure

During the ECT measurement, the stacked aluminum blocks are clamped in the chuck apparatus (see Fig. 2b). The ECT probe is positioned at specified points with equidistant distances of Δx=5 mm between the positions in the x direction on the surface of the specimen (stacked aluminum blocks) as illustrated in Fig. 1b. The slit defect ranges from x=25 to x=125 mm. In a range of $x=-\mathrm{50}$ to x=75 mm, the impedance of the ECT probe is measured with the excitation frequency f_exc=100 Hz and averaged over a certain time. Preceding investigations using excitation frequencies from the range 10–1000 Hz in the ECT measurement setup have shown that the excitation frequency f_exc=100 Hz is the lowest frequency at which the measured signals due to noise can be interpreted accordingly. For lower frequencies it was not possible to extract a defect signal due to the noise. For higher frequencies no better results concerning the defect detection limit could be achieved. For the excitation frequency used f_exc=100 Hz, the skin depth δ for the investigated Al alloy is approximately 11 mm. The I/O ports of the ELOTEST N300 are used to measure the impedance with the BNC-2120 module from National Instruments (2012). The measurements are repeated for both setups with and without defects. The signals obtained are amplified in the measurement system. An optimal amplification was determined to use as much of the measurement range as possible, achieving a maximal sensitivity. Once this amplification factor was determined, it is used for one depth configuration with and without defects to achieve comparability between the measured signals.

4 Results

In the following, a comparison between LET and ECT measurements with focus on the detection depth of both methods is presented.

All LET measurements are performed with an axially magnetized NdFeB cylinder magnet of material grade N52, with diameter D_mag=29 mm and height 10.7 mm. There are several reasons for using the velocity v=300 mm s⁻¹ in the LET measurements and an excitation frequency of f_exc=100 Hz. The velocity is set to this value because the weight forces of the magnet and the mechanical assembly fixing the magnet at the force sensor, as well as the lift force, act on the force sensor. Increasing the velocity might result in destruction of the force sensor, especially when passing the edges of the specimen, where the lift force reaches its maximum.

In order to compare LET and the classical ECT in terms of frequency range, the following analogy for LET is used. It is assumed that the magnetic field of the PM is homogeneous directly below the magnet. When the magnet passes by the edge of the defect, it can be interpreted as a rectangular pulse of the excitation magnetic field. The excitation pulse width T corresponds to the magnet diameter (D_mag=29 mm) in relation to the used velocity (v=300 mm s⁻¹), and it can be calculated as $T=D_{\mathrm{mag}}/v=\mathrm{0.097}$ s. The frequency spectrum A(f) of the rectangular pulse can be determined according to Bracewell (2000) as

$$\begin{array}{}\text{(1)}& A\left(f\right)=T\mathrm{sinc}\left(Tf\right).\end{array}$$

The frequency spectrum of the rectangular pulse is a continuous function. However, to compare the LET setup with the classical ECT the single frequency corresponding to the first extremum of the spectrum, equal to $f_{\mathrm{1}}\approx \mathrm{3}/\left(\mathrm{2}T\right)\approx \mathrm{15.5}$ Hz, is introduced. The frequency f₁ can be interpreted as an equivalent excitation frequency for the LET method. Using the equivalent frequency, the skin depth can be calculated as

$$\begin{array}{}\text{(2)}& \mathit{\delta }=\sqrt{{\displaystyle \frac{\mathrm{1}}{\mathit{\pi }{f}_{\mathrm{1}}{\mathit{\mu }}_{\mathrm{0}}\mathit{\sigma }}}}=\mathrm{27.7}\mathrm{mm}\end{array}$$

for the used LET setup. Similarly, for the ECT setup with an excitation frequency 100 Hz, the corresponding standard skin depth given by Eq. (2) equals δ=10.9 mm.

It should be mentioned that the standard skin depth is determined assuming that a plane electromagnetic wave is incident perpendicularly on a conducting half-space. Mottl (1990) showed that the true skin depth for an air-cored ECT excitation coil depends on the size and shape of the probe. The mean coil radius of the used ECT probe is in the range of the skin depth. According to Mottl, the standard skin depth in such a case is almost 2 times larger than the true skin depth. However, due to the complex internal structure of the ECT probe used (Porzig et al., 2014), the correction suggested by Mottl cannot be directly applied. To compare both methods in a similar way, the standard formula (2) is used with awareness that the skin depth for the ECT setup is overestimated.

It can be observed that the equivalent LET frequency is much smaller than the excitation frequency used in the ECT setup.

In order to reduce this difference, either the velocity in the LET setup has to be increased or the excitation frequency in ECT has to be decreased. However, due to the fact that both of the used measurement systems operate at their limits, it is not possible to perform the suggested adjustment of the setup parameters. In the case of LET, mechanical oscillations and the measurement range of the force sensor limit the maximum velocity for the actual setup. Otherwise, the conventional ECT system used enables excitation frequencies down to 10 Hz. However, due to noise, evaluable signals can only be acquired for an excitation frequency above 100 Hz.

Furthermore, the mechanical fixation of the specimen on the x drive limits the lift-off to h=1 mm. The measurement is repeated 15 times and as a next step is averaged to reduce random errors in the data.

Previous investigations on LET showed that the lift force F_z is the most sensitive force component to detect defects. This is the reason why only F_z is shown in the measurement results in order to investigate the detection limit of LET. Figure 3 shows the run of the lift force over the whole specimen length starting from negative x. It can be noted that there is a force deviation at the edges of the specimen at $x=\pm \mathrm{125}$ mm and at the edge of the slit at x=25 mm. For every defect depth the assembly of the specimen changes, as shown in Fig. 1b. The height d of the Al block on top of the assembly influences the lift force signal at the edges of the specimen. Additionally, the slit is located at the end edge of the specimen. Hence, these two effects result in the various differences in the lift force at the front and the end edge of the specimen. In addition Fig. 3 shows that the deviation at the edge of the slit decreases with increasing defect depth d.

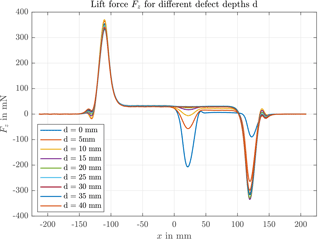
Figure 3 Measured lift force F_z in LET measurement of different specimens with different slit defect depths d.

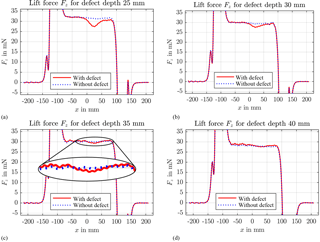
Figure 4 Measurement results of the lift force F_z with (solid red line) and without a defect (dotted blue) for the defect depths d=25 mm, d=30 mm, d=35 mm, and d=40 mm.

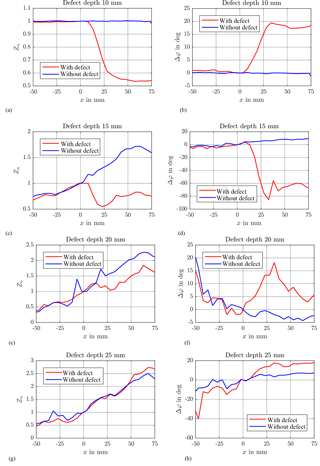
Figure 5 Normalized impedance Z_n and phase difference for defect depths of d=10 mm (a, b), d=15 mm (c, d), d=20 mm (e, f), and d=25 mm (g, h) for specimens with a defect (red solid line) and without a defect (blue solid line) of the ECT measurement.

In order to figure out the detection depth of LET with the measurement setup described above, we compare the measurement results of the measurements with and without defects. The results of the measurements for the defect depths d=25 mm up to d=40 mm are presented in Fig. 4. It can be noticed that the difference between the two signals decreases with an increasing defect depth. In the case of a defect depth d=25 mm the lift force before the slit is higher than the lift force when the magnet is above the slit. This effect cannot be noticed anymore for deeper lying defects. The most significant deviation of the measured force in the case of the specimen with a defect can be seen at the edge of the defect at x=25 mm. On this basis we can state that the defect is still detectable in a depth of 35 mm. In the case of a defect depth d=40 mm it is not possible to distinguish whether the perturbation in the signals results from the defect or an influence of the measurement system itself. So it can be declared that the detection limit of LET in the examined material scenario is between 35 and 40 mm.

The differences between the measurements with and without defects – except for the perturbation at the edge of the defect – result from slight lift-off differences of the z-axis adjustment.

As already mentioned, f_exc=100 Hz was the lowest usable frequency for ECT, resulting in the best results for the detection limit. Hence, only these best results for this single frequency are shown in the following.

For comparison of the ECT measurements, the amplitude of the impedance for each depth is normalized with respect to the value measured in the center of the defect-free specimen at x = 0 mm. Additionally, the phase was shifted in such a way that at the same position in the center, in the case of no defect, the phase has zero degrees.

In Fig. 5, the measured normalized impedance $Z_{\mathrm{n}}=\left|\underset{\mathrm{¯}}{Z}\left(x\right)/\underset{\mathrm{¯}}{Z}(x=\mathrm{0})\right|$ (panels a, c, e, and g) and the measured phase difference Δφ (panels b, d, f, and h) measured with the ECT coil are shown WRT the coil's position x for defect depths d=10 mm up to d=25 mm. It can be seen that the edge of the slit at $x=+\mathrm{25}$ mm is still detectable for a defect depth of d=15 mm mainly due to a change in the phase (Fig. 4d). For defect depths of d=0 and 5 mm (not shown here) a strong change in the phase, but also in the impedance, is recognized at the edge of the slit at $x=+\mathrm{25}$ mm. In the case of the defect at depth d=20 mm, there is a slight change of impedance or a phase shift visible at the edge of the defect. For a defect depth d=25 mm the impedance is slightly increasing with and without defects – the signals are somehow parallel to each other but no indication of the defect is possible. The slight variations in the phase that can be seen in Fig. 5h are a result of the noise due to the amplification used.

Hence, the detection limit for the ECT probe is at d=20 mm.

5 Conclusions

In this study, the detection limit of the LET setup is determined and compared to ECT measurements performed with the commercial ECT measurement device ELOTEST N300 from Rohmann GmbH. The LET measurement data are acquired with the multi-measurement platform BASALT-C MMP-15 which is available at the Advanced Electromagnetics Group at the Technische Universität Ilmenau. The basic principles as well as the measurement setups and the measurement procedures are described.

The different excitation mechanisms and the corresponding frequency ranges for both setups used have been discussed. The LET technique is well suited for the detection of deep buried defects due to its low equivalent frequency.

In addition, it can be stated that both methods are complementary, considering the equivalent LET frequency and the excitation frequency for ECT. LET enables the detection of defects, whereby in the classical ECT a very low excitation frequency should be applied. However, this is challenging due to noise and demands complex and sophisticated signal acquisition and processing. The measurement results show that it is possible to detect the slit defect in a depth of 35 mm in the case of LET and at 20 mm in the case of ECT, which is in agreement with the discussion about the frequency range for both methods.

It should also be mentioned that deeper lying defects could be detected with a better and specially optimized ECT measurement setup (Mook et al., 2006). Finally, LET as a motion-induced technique is especially of interest for applications with moving objects as often found in production lines in industry.