the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Combined distributed Raman and Bragg fiber temperature sensing using incoherent optical frequency domain reflectometry
Stefan Werzinger
Thomas Ringel
Peter Bechtold
Torsten Thiel
Rainer Engelbrecht
Thomas Bosselmann
Bernhard Schmauss
Optical temperature sensors offer unique features which make them indispensable for key industries such as the energy sector. However, commercially available systems are usually designed to perform either distributed or distinct hot spot temperature measurements since they are restricted to one measurement principle. We have combined two concepts, fiber Bragg grating (FBG) temperature sensors and Raman-based distributed temperature sensing (DTS), to overcome these limitations. Using a technique called incoherent optical frequency domain reflectometry (IOFDR), it is possible to cascade several FBGs with the same Bragg wavelength in one fiber and simultaneously perform truly distributed Raman temperature measurements. In our lab we have achieved a standard deviation of 2.5 K or better at a spatial resolution in the order of 1 m with the Raman DTS. We have also carried out a field test in a high-voltage environment with strong magnetic fields where we performed simultaneous Raman and FBG temperature measurements using a single sensor fiber only.
- Article
(7033 KB) - Full-text XML
- BibTeX
- EndNote
An important application for fiber sensors is temperature monitoring. One of the main advantages of fiber optic temperature sensors is that long distances can be covered and that the sensor fibers are insensitive to electromagnetic fields. This allows fiber optic sensors to be employed in all kinds of industrial environments and energy facilities (Hu et al., 2011). Several sensors can be cascaded or multiplexed to measure at a series of distant locations using only a single, centrally installed measurement unit, which reduces costs and complexity.
There are various different measurement concepts that are either based on temperature-dependent scattering phenomena (Rayleigh, Brillouin, Raman scattering; Ukil et al., 2012) or employ distinct temperature sensitive fiber components such as fiber Bragg gratings (FBGs; Kersey et al., 1997).
While scattering-based concepts enable truly distributed temperature sensing (DTS), FBG sensors are better suited for the monitoring of hot spots at distinct positions with a good temperature resolution.
Zaidi et al. (2012) combined Raman DTS and FBGs for dynamic strain sensing. However, they used two separate fibers (single-mode for FBGs, multimode for Raman DTS) and a time domain interrogation approach which was not suitable to measure the absolute Bragg wavelength.
We have combined Raman-based DTS with FBG temperature sensors in one measurement setup which relies on incoherent optical frequency domain reflectometry (IOFDR), which is implemented with a tunable laser source (TLS) for interrogation and uses only one single-mode fiber (Köppel et al., 2017).
2.1 Spatially resolved backscatter and reflection measurements with incoherent optical frequency domain reflectometry
For both concepts, Raman DTS and FBG temperature sensing, a method to spatially resolve the backscattered and reflected light along the fiber is needed. In a Raman DTS system, the temperature measurement is based on the power ratio of the Raman Stokes and anti-Stokes backscattering components, whereas for the FBG sensors the spatial resolution, in addition to the wavelength resolution, is crucial to separate the individual FBG sensors.
Conventional optical time domain reflectometry (OTDR) systems launch an optical pulse into the fiber and measure the backscattered and reflected light over time. This so-called impulse response hF(t) can be related to spatial fiber coordinates via the group velocity of light in the fiber resulting in a backscattering/reflection profile R(z).
However, the same information can be obtained by measuring the frequency response HF(f) of the sensor fiber and calculating hF(t) via the inverse Fourier transform (IFT) as depicted in Fig. 1. This approach is called IOFDR and offers various advantages over OTDR, such as a lower peak-to-average power ratio and accurate calibration capabilities. A higher average power leads to a better signal-to-noise ratio, whereas calibration techniques allow the full available bandwidth of the components to be used and non-idealities in their frequency response to be compensated.
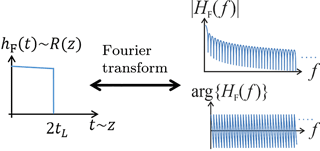
Figure 1Relation between backscatter profile/impulse response and frequency response for an ideal fiber.
IOFDR was first used as an alternative to OTDR for fiber fault detection (Ghafoori-Shiraz and Okoshi, 1985). Later, it was also proposed for various fiber sensing applications, including Raman DTS (Karamehmedovic and Glombitza, 2004), distributed strain sensing in polymer optical fibers (Liehr et al., 2009), and FBG multiplexing (Chan et al., 1999).
We have applied the IOFDR concept for combined FBG temperature and Raman DTS measurements in one setup for the first time to the best of the authors' knowledge.
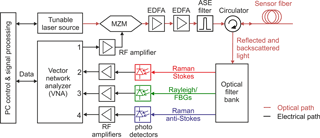
2.2 Experimental IOFDR system setup
IOFDR allows a continuous-wave (CW) light source to be employed, resulting in a much lower peak-to-average power ratio in the fiber compared to pulsed operation. However, in order to avoid self-stimulated Brillouin backscattering which would limit the maximum CW optical launch power, it is necessary to spectrally broaden the laser source. We use phase modulation with a noise signal to broaden the laser source to a linewidth of around 6 GHz. This is significantly broader than the Brillouin gain spectrum which has a width in the order of tens of MHz for a standard single-mode fiber. Therefore, Brillouin scattering is effectively suppressed for the fibers and launch powers used in our setup. Moreover, this ensures that the light source operates in the incoherent regime with a sufficiently small coherence length while keeping the wavelength accuracy of a narrow-band laser.
In order to measure the frequency response HF(f) of a sensor fiber, the CW light source is intensity-modulated with frequencies up to about 100 MHz with the stimulus signal of a vector network analyzer (VNA) via a Mach–Zehnder modulator (MZM).
In the sensor fiber, light is backscattered by Rayleigh and Raman scattering or reflected by FBGs. Some of this light is guided in the backward direction in the fiber and eventually separated using a circulator. An optical filter bank is used to split it up into the different spectral components resulting from FBG reflections/Rayleigh and Raman scattering. Each spectral component is detected with a fast photodiode. The electrical output signal of the detectors is amplified and fed into the VNA again, which determines the amplitude and phase relative to the electrical stimulus signal that was used to modulate the pump light (see Fig. 2).
Measuring this complex-valued transfer function at many uniformly spaced frequencies and normalizing it to a reference trace gives the discrete frequency response HF(f) of the sensor fiber. Calculating an IFT yields the corresponding impulse response hF(t) in the time domain. The whole experimental measurement system was installed in a portable rack (see Fig. 3), which allows it to be employed flexibly.
As the limited electrical measurement bandwidth resembles a rectangular window in the frequency domain, a sinc-shaped reconstruction kernel occurs in the time domain (Harris, 1978). Optionally, the measured frequency response can be multiplied by other window functions before the transformation into the time domain in order to suppress side lobes in the vicinity of reflections.
From the reflection/backscatter impulse response hF(t) the reflection/backscatter profile R(z) is obtained by estimating the DC component and rescaling the abscissa using
where vg is the effective group velocity in the sensor fiber. The DC component HF(f=0) corresponds to an upshift of the reflection/backscatter profile and cannot be measured directly with the VNA. However, it can be accounted for by subtracting the noise floor offset after the end of the fiber where the mean backscatter level must be zero.
The nominal achievable spatial two-point resolution Δz for this approach is given by (Iizuka et al., 1984)
where B is the electrical measurement bandwidth of the VNA. This value corresponds to the distance between the first zero crossings of the sinc reconstruction kernel if no window is applied and is often presented for comparison. However, even small reflections, e.g., at fiber connectors, cause side lobe artifacts that must be suppressed with the help of an effective window at the cost of a decreased effective spatial resolution.
The maximum unambiguous measurement range zmax for a given bandwidth B is limited by the number of measurement frequencies N, yielding (Iizuka et al., 1984)
with Δf resembling the frequency step size of the VNA.
For Raman DTS measurements a frequency step size of 30 kHz and a maximum modulation frequency of 99.99 MHz was used. These parameters yield a maximum unambiguous measurement range zmax of almost 3.5 km and a nominal spatial resolution Δz of around 1 m. However, due to the Blackman window of (even) length N,
which was applied in all presented measurements to reduce side lobe effects; the 3 dB width (referring to optical reflectivity) of the main lobe is broadened by a factor of 2.35 (Harris, 1978).
The 10 to 90 % rise time or distance is another common measure for spatial resolution in DTS systems. In our lab measurement, the 10 % to 90 % rise distance was experimentally determined to be 1.3 m for the 80 ∘C trace.
For the FBG temperature sensing the effective resolution is given by the physical length of the FBG in the fiber, which is around 5 mm for the FBGs that we used. The IOFDR resolution must only be high enough to distinguish multiple FBGs which use the same Bragg wavelength. However, in this case no IFT was applied but instead a model-based approach was used which does not require prior windowing (Werzinger et al., 2017).
FBGs are point sensors for temperature measurements and therefore suitable for selective thermal hot spot monitoring. Their periodic refractive index modulation causes a narrowband back reflection at the so-called Bragg wavelength given by the Bragg condition λB=2neffΛ, where neff is the effective refractive index of the fiber and Λ the grating period. Both of these parameters depend on temperature and strain, resulting in a shift of the Bragg wavelength relative to the wavelength λB0 at a reference temperature T0 and strain. In order to measure temperature changes only, it is necessary that the FBGs are either strain-compensated or mechanically decoupled from any strain.
Generally, the temperature dependence of the Bragg wavelength follows a nonlinear function (Filho et al., 2014), which is usually expanded into a Taylor series:
In many applications, the linear temperature coefficient is sufficiently accurate. However, for wide temperature ranges and better accuracy, higher order terms should be taken into account in the calibration process.
In our system, the Bragg wavelength of a FBG sensor is determined by examining the reflectivity during a stepped wavelength scan of a tunable laser source (TLS; Werzinger et al., 2016). An array of several FBGs with the same or similar Bragg wavelengths can be separated spatially by performing IOFDR measurements at each wavelength step.
The spectral signatures of the gratings are reconstructed using a model-based compressed sensing approach (Werzinger et al., 2017), where the fixed positions of the FBGs are used as prior knowledge and the reflectivities are estimated directly from the measured frequency response without performing an IFT.
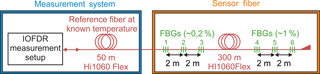
Two FBG arrays, each containing three gratings in a spacing of 2 m, were fabricated in a HI1060 FLEX single-mode fiber, which was subsequently recoated. The first grating array was fabricated without hydrogen loading, reaching reflectivities of ∼ 0.2 %, whereas for the second grating array a hydrogen-loaded fiber was used, resulting in reflectivities of ∼ 1 %. The low reflectivities were chosen to suppress any crosstalk effects like multiple reflections and spectral shadowing, which occur if the Bragg wavelengths of the FBGs overlap (Cooper et al., 2001).
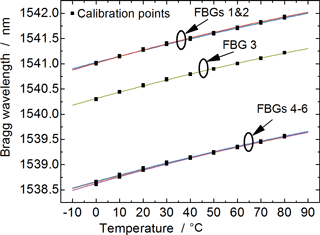
Prior to the temperature measurements, a calibration of the Bragg wavelengths over temperature was performed. Therefore, the gratings were installed in a temperature control unit with thermoelectric coolers, and 10 temperature cycles ranging from 0 to 80 ∘C in steps of 10 K were run.
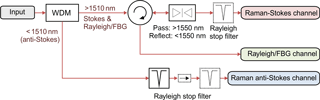
Figure 5Setup of the filter bank that is used to separate the Raman components and the FBG reflections (the dashed components were added for improved isolation in the field test measurements).
The Bragg wavelengths are determined from the reconstructed reflectivity profiles by a Gaussian fit with a threshold of 20 % (see calibration points in Fig. 4). At a temperature of 20 ∘C, the grating array with lower reflectivities (labeled FBG 1–3) contains one FBG with a Bragg wavelength of 1540.6 nm and two gratings at 1541.3 nm, whereas all FBGs of the second array (labeled FBG 4–6) are centered around 1538.9 nm. These differences are probably due to the hydrogen treatment of the second grating array prior to the fabrication and increased fabrication tolerances at low reflectivities.
Looking closer at the calibration points in Fig. 4, a slightly nonlinear characteristic can be observed towards lower temperatures. Therefore, a second-order polynomial was fitted to the calibration data (see Fig. 4).
The average root mean square error (RMSE) of the calibration curves is approximately 8 pm, which would correspond to a temperature uncertainty of about 0.6 to 0.7 K for these gratings.
Raman scattering of light in a fiber causes a Stokes wave and an anti-Stokes wave at wavelengths above and below the pump wavelength that can be observed in the backscattered light. The center frequencies of these components are shifted by the frequency of the molecule vibrations fvib in the fiber. In silica fibers, fvib is about 13 THz (Engelbrecht, 2014), leading to a wavelength shift of approximately 100 nm at a pump wavelength λ0 of 1540 nm. Moreover, a spectral broadening occurs due to the interaction between the molecules in a solid medium. The resulting spectra of the two Raman components can be separated with an optical filter bank. Due to the temperature dependence of the occupation of the energy states in silica, the ratio between the intensity of the anti-Stokes wave IAS,0 and the Stokes wave IS,0 is also dependent on temperature (Engelbrecht, 2014; Dakin et al., 1985):
In Eq. (6), fAS and fS are the frequencies of the anti-Stokes and Stokes wave, respectively, h is Planck's constant and k is Boltzmann's constant.
For a practical application, Eq. (6) must be extended due to the wavelength dependence of the backscatter capture fraction η in a fiber and the differences in the detector sensitivity Rresp. Neglecting the slightly differing fiber attenuation for the Raman components yields
The proposed filter bank setup to separate the Raman Stokes, Raman anti-Stokes backscattering and FBG reflections, designed for a pump wavelength of 1540 ± 2 nm, is shown in Fig. 5.
At the input of the filter bank, the Raman anti-Stokes component, which generally has the lowest power, is split off by a wavelength division multiplexer (WDM). Because of the limited isolation between the WDM outputs, a FBG-based stop filter is necessary in the Raman anti-Stokes channel to block Rayleigh backscatter and the relatively strong FBG reflections in the pump wavelength window. The spectral Rayleigh/FBG content is split off by employing a long-pass edge filter, which is installed after a circulator. The Raman Stokes component can be detected at the output of the long-pass filter.
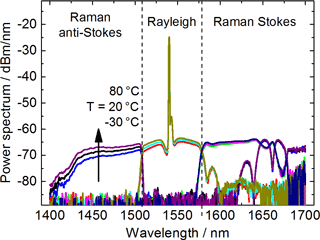
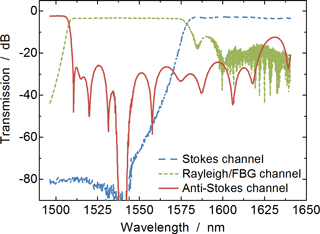
Figure 6Measured backscattering spectra at the filter bank outputs (before enhancement) for a 300 m HI1060 FLEX fiber (resolution bandwidth: 1 nm).
In Fig. 6, the attenuation-compensated spectra at the outputs of the initial filter bank, measured with an optical spectrum analyzer, are depicted for a 300 m long HI1060 FLEX fiber at three different temperatures. This fiber is especially well suited for Raman DTS since it exhibits a relatively high amount of Raman scattering (Engelbrecht, 2014). The various backscattering components and the temperature dependence of the Raman anti-Stokes power density is clearly visible.
With our initial setup used for the lab experiment, a very good isolation between the Rayleigh/FBG channel and the two Raman channels of about 70 dB was achieved.
However, due to the large differences in power between the reflections of the FBGs (reflectivities up to approximately −20 dB) and the Raman backscattering (around −90 dB for a 1 m fiber segment) we have enhanced the isolation between the filter channels by additional FBG-based stop filters in the Raman channels for the field test. The transmission characteristics of the enhanced filter bank setup are depicted in Fig. 7.
Furthermore, there is some extent of crosstalk between the channels. Especially the non-ideal separation of the Raman channels must be considered when the temperature is calculated. Moreover, the two filter channels for the Raman components will generally experience different attenuations, aAS and aS. Therefore, the measured ratio of power in the anti-Stokes and Stokes wave can be expressed as
where x is the factor of coupling from the Stokes into the anti-Stokes channel. The various factors can be replaced by two calibration coefficients, C1 and C2:
The coefficients C1 and C2 can be determined from calibration sections where the fiber has a known temperature. For a given temperature T and a fixed (measured) ratio , Eq. (9) resembles a linear regression problem. To find C1 and C2 a standard least-squares algorithm is employed.
Eventually, rearranging Eq. (9) gives the temperature profile T(z) along the fiber in dependence of the measured, spatially resolved backscatter ratio at the outputs of the filter bank:
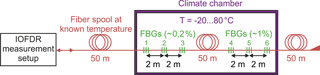
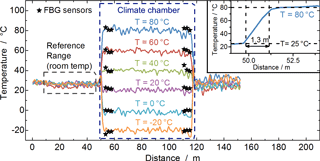
We prepared a sensor fiber, which consisted of the aforementioned FBG arrays spliced to either end of a 50 m HI1060 FLEX single-mode fiber and put it into a climate chamber. Before and after the sensor fiber, a 50 m launch fiber of the same type was used (see Fig. 8). At the end of the fiber chain, a short piece of coreless fiber served as termination.
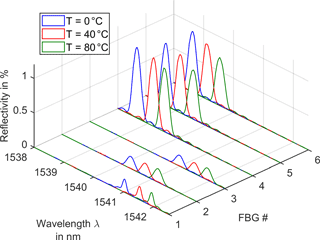
Figure 9Examples of reconstructed FBG reflectivities at three different temperatures using model-based compressed sensing.
Initially, the whole setup was left settled at room temperature and a reference measurement was performed. From the acquired reflection/backscatter profile, the connector losses between the fiber segments were determined.
Subsequently, the climate chamber was set to temperatures ranging from −20 to 80 ∘C in steps of 20 K. For each temperature step, the TLS performed a wavelength sweep from 1538 to 1542.5 nm (step size: 20 pm) and the frequency response of the Rayleigh/FBG channel was measured with the VNA at each wavelength step (see Table 1 for VNA parameters). From the acquired data set, the spectral shapes of all FBGs were reconstructed (see Fig. 9), the Bragg wavelengths were determined, and the corresponding temperatures were calculated using the calibration curves depicted in Fig. 4.
Table 1VNA measurement parameters for the Raman DTS and FBG temperature sensor measurements in the lab experiment.

The Raman measurements were performed at different wavelengths around 1540 nm, where the FBGs showed little reflectivity, in order to minimize their influence. The Raman Stokes and anti-Stokes backscatter profiles along the fiber were reconstructed applying the inverse fast Fourier transform (IFFT) to the frequency response determined at the corresponding filter bank outputs. Before the calculation of the IFFT, a Blackman window function was applied to suppress unwanted side lobes. From the backscatter profiles, the temperature profile was calculated according to Eq. (10).
The room temperature was recorded and the 50 m lead fiber was used to estimate the required calibration coefficients C1 and C2 with a least-square-error fit for each measurement.
For the FBG reconstruction, the model-based compressed sensing approach (Werzinger et al., 2017) was chosen, which allowed the same modulation bandwidth to be used as for the Raman DTS (only 100 MHz). For the lab measurements, the fiber launch power was approximately 26 dBm.
The results of the FBG and Raman temperature measurements are depicted in Fig. 10. A good agreement was found between the temperatures measured with the FBG sensors and the Raman DTS results. In the Raman DTS measurements, an average uncertainty better than 1 K (over all climate chamber measurements), a worst-case standard deviation of around 2.5 K for the measurement at 80 ∘C, and on average a standard deviation of 1.5 K was achieved for the sensor fiber inside the climate chamber. The 10 to 90 % rise distance was found to be 1.3 m in the 80 ∘C trace (see Fig. 10).
To verify the functionality of our system under realistic operating conditions, we have carried out a field test in a high-voltage test environment. The device under test was a high-power choke coil made of aluminum with a diameter of around 2.3 m, a height of around 2.9 m, and a nominal inductance of 9 mH at operating currents up to 2100 A and voltages up to 15 kV.
For this experiment, we used the two aforementioned sets of three FBGs and a 300 m long HI1060 Flex single-mode fiber in between (see Fig. 11). The sensor fiber was wound around the coil from top to bottom in around 40 windings and the FBGs were attached vertically at the coil (see Fig. 12). The FBGs were attached to the coil using a heat transfer compound in order to assure good thermal contact and minimize the strain on the fiber. Additionally, a commercially available GaAs bandgap temperature sensor was installed close to FBG 4 (see Fig. 12) for comparison.

Figure 12Installed fiber at the high-power coil for the high-voltage field test ((a) schematic, (b) picture).
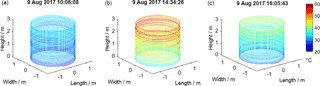
Figure 13Temperature distribution along the fiber wound around the coil shortly after turning on the current (a), when heated up (b), and after cooling down for more than 1 h.
Table 2VNA measurement parameters for the Raman DTS and FBG temperature sensor measurements in the field test.

Compared to the laboratory experiment, the measurement system was slightly modified: the avalanche photodiode detectors for the detection of the Raman components were replaced with more sensitive ones that give a better signal-to-noise ratio and allowed the optical launch power to be reduced and the VNA parameters to be adjusted (see Table 2) for faster measurements. Moreover, the filter bank was upgraded with two additional filters to further enhance the isolation between the Raman and the FBG/Rayleigh channel. This allowed us to average the traces acquired during the wavelength scan over all wavelengths and use them for the Raman DTS. The optical launch power into the sensor fiber was reduced to approximately 23 dBm.
At the beginning of the test, no current was flowing through the coil and it was in a thermal equilibrium at room temperature (approximately 25.5 ∘C). After switching on, a current of 400 A was flowing in approximately the first 4 min before it was increased to around 975 A within 3 min. After approximately 5 h, the current was switched off and the coil was allowed to cool down again. During the test, the measurement setup remained unchanged. The same VNA measurement parameter set was used for the determination of the temperatures based on Raman DTS and FBG sensors.
For the Raman DTS, the measured frequency traces were averaged over all probe wavelengths before computing the backscatter profile for the Raman Stokes and anti-Stokes component via IFFT.
Although the 300 m fiber segment and the 50 m launch fiber were both HI1060 Flex fibers, we found they had different properties possibly due to aging or batch-to-batch variation, since the 300 m fiber was much older and had been used in many temperature experiments before. Especially the different attenuation of Raman Stokes and anti-Stokes wavelengths is problematic because it skews the ratio profile . We have therefore used a measurement that was taken before the test when the coil was in thermal equilibrium to determine the tilt resulting from the different attenuation and to compensate for it in all other measurements.
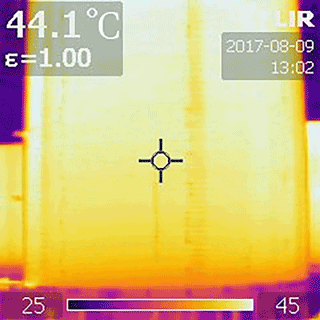
Figure 14Thermal image of the coil when it was heated up (no temperature calibration due to unknown emissivity).
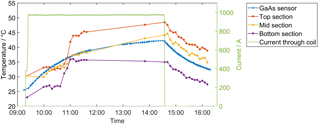
Figure 15Temporal change of the temperature measured with Raman DTS at three different locations of the coil (mean of two windings at the top, middle, bottom) and the GaAs sensor measurements for reference.
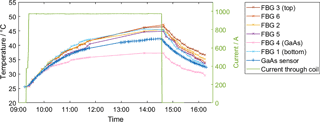
Figure 16Temporal change of the temperature measured with the FBGs at six different locations of the coil and the GaAs sensor measurements for reference.
The calibration sections to determine the coefficients C1 and C2 in Eq. (9) were a short segment of the 300 m fiber before the coil that was at room temperature and the section at the GaAs temperature sensor.
The resulting temperature distribution for three instances of time mapped onto a cylinder representing the coil is depicted in Fig. 13. It can be seen that the coil gets warmer at the top and that there is a temperature gradient towards the bottom windings. This is confirmed by an image of the heated coil taken with a thermal camera (see Fig. 14).
Figure 15 represents the temporal change of temperature for three different fiber segments (each averages over two windings of fiber) corresponding to the top, middle, and lower part of the coil. Furthermore, the read-outs of the GaAs sensor and the current through the coil are plotted. Interestingly, a decrease of the temperature in all segments can be observed between 10 and 11 h. This is probably due to ventilation in the test site at that time, which was also observed by the experimenters. The GaAs sensor was attached to the heat transfer compound covered by tape, which probably prevented the corresponding spot from cooling down.
The temporal evolution of the measured FBG temperatures is depicted in Fig. 16. The temperature of the GaAs sensor before the warm-up is taken as an initial reference for all FBGs. Like the Raman measurement, the temperatures of the FBGs at the top of the coil (FBG 3 and FBG 6) reach the highest temperature (∼ 46 ∘C) and there is a decreasing trend towards the bottom (∼ 35 ∘C). However, the temperature of FBG 1 (bottom) exceeds that of FBG 4 (nearby GaAs sensor) significantly. This outlier is probably caused by additional strain on the fiber due to thermal expansion of the coil, which in turn increased the temperature sensitivity. Considering that the typical strain sensitivity of a FBG is ∼ 1 pm/µε, strain-induced errors of a few Kelvins can occur even at small strains below 100 µε. This effect is not due to a failure of the measurement system though and can be mitigated by improved packaging of the FBGs to make sure mechanical stress cannot disturb the measurement.
In this work, we have successfully demonstrated a fiber optical temperature measurement system based on IOFDR, which combines FBG temperature sensors and Raman-based DTS to enable both distinct hot spot and truly distributed temperature profile measurements over a wide range of temperatures, with a 10 to 90 % rise distance of around 1 m. We have also demonstrated that there are no general restrictions for using our system in a high-voltage environment.
Future work is planned to address the electrical components in our system. Instead of a costly and feature-rich vector network analyzer, a custom-made solution would be desirable to reduce the system cost, size, and complexity while potentially increasing the measurement speed. Furthermore, possible benefits of the combination of the measurement data from Raman DTS and FBGs, such as temperature-compensated strain measurements with FBGs, should be evaluated.
The underlying measurement data are not publicly available and can be requested from the authors if required.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Sensor/IRS2 2017”. It is a result of the AMA Conferences, Nuremberg, Germany, 30 May–1 June 2017.
Parts of this work were funded by the German Federal Ministry for Economic Affairs and Energy (BmWE) under the grant no. 03ET7522B (project “iMonet”).
We would like to thank the Siemens AG (Nuremberg, Germany) and
especially Uemit Genc for the cooperation and the participation in the field
test.
Edited by: Werner Daum
Reviewed by: three anonymous referees
Chan, P. K., Jin, W., Gong, J., and Demokan, N.: Multiplexing of fiber Bragg grating sensors using a FMCW technique, IEEE Photonic. Tech. L., 11, 1470–1472, 1999.
Cooper, D. J. F., Coroy, T., and Smith, P.W. E.: Time-division multiplexing of large serial fiber-optic Bragg grating sensor arrays, Appl. Opt., 40, 2643–2654, https://doi.org/10.1364/AO.40.002643, 2001.
Dakin, J. P., Pratt, D. J., Bibby, G. W., and Ross, J. N.: Distributed optical fibre Raman temperature sensor using a semiconductor light source and detector, Electron. Lett., 21, 569–570, https://doi.org/10.1049/el:19850402, 1985.
Engelbrecht, R.: Stimulierte Raman-Streuung, in: Nichtlineare Faseroptik, Springer, Berlin Heidelberg, Germany, 205–282, https://doi.org/10.1007/978-3-642-40968-4, 2014.
Filho, E., Baiad, M., Gagné, M., and Kashyap, R.: Fiber Bragg gratings for low-temperature measurement, Opt. Express, 22, 27681–27694, https://doi.org/10.1364/OE.22.027681, 2014.
Ghafoori-Shiraz, H. and Okoshi, T.: Optical-fiber diagnosis using optical frequency-domain reflectometry, Opt. Lett., 10, 160–162, 1985.
Harris, F. J.: On the use of windows for harmonic analysis with the discrete Fourier transform, Proc. IEEE, 66, 51–83, https://doi.org/10.1109/PROC.1978.10837, 1978.
Hu, C., Wang, J. Zhang, Z., Jin, S., and Jin, Y.: Application research of distributed optical fiber temperature sensor in power system, Asia Communications and Photonics Conference and Exhibition (ACP), Shanghai, 2011, 1–6, https://doi.org/10.1117/12.905303, 2011.
Iizuka, K., Freundorfer, A. P., Wu, K. H., Mori, H., Ogura, H., and Nguyen, V.-K.: Step-frequency radar, J. Appl. Phys., 56, 2572–2583, https://doi.org/10.1063/1.334286, 1984.
Karamehmedovic, E. and Glombitza, U.: Fiber optic distributed temperature sensor using incoherent optical frequency domain reflectometry, Proc. SPIE 5363, Emerg. Optoelectron. Appl., 107–115, 2004.
Kersey, A. D., Davis, M. A., Patrick, H. J., LeBlanc, M., Koo, K. P., Askins, C. G., Putnam, M. A., and Friebele, E. J.: Fiber grating sensors, J. Lightwave Technol., 15, 1442–1463, https://doi.org/10.1109/50.618377, 1997.
Köppel, M., Werzinger, S., Engelbrecht, R., Sutter, J.-R., Bergdolt, S., and Schmauss, B.: Incoherent Optical Frequency Domain Reflectometry for Distributed Raman and Bragg Fiber Temperature Sensors, in: Proceedings of the AMA Conferences 2017 with SENSOR and IRS2, SENSOR 2017, 18th International Conference on Sensors and Measurement Technology, edited by: AMA Service GmbH, SENSOR 2017, Nürnberg, 30 May–1 June 2017, AMA Service GmbH, Wunstorf, 261–266, 2017.
Liehr, S., Lenke, P., Wendt, M., Krebber, K., Seeger, M., Thiele, E., Metschies, H., Gebreselassie, B., and Munich, J. C.: Polymer Optical Fiber Sensors for Distributed Strain Measurement and Application in Structural Health Monitoring, IEEE Sens. J., 9, 1330–1338, https://doi.org/10.1109/JSEN.2009.2018352, 2009.
Ukil, A., Braendle, H., and Krippner, P.: Distributed Temperature Sensing: Review of Technology and Applications, IEEE Sens. J., 12, 885–892, https://doi.org/10.1109/JSEN.2011.2162060, 2012.
Werzinger, S., Bergdolt, S., Engelbrecht, R., Thiel, T., and Schmauss, B.: Quasi-Distributed Fiber Bragg Grating Sensing Using Stepped Incoherent Optical Frequency Domain Reflectometry, J. Lightwave Technol., 34, 5270–5277, https://doi.org/10.1109/JLT.2016.2614581, 2016.
Werzinger, S., Gottinger, M., Gussner, S., Bergdolt, S., Engelbrecht, R., and Schmauss, B.: Model-based compressed sensing of fiber Bragg grating arrays in the frequency domain, Proc. SPIE 10323, 25th International Conference on Optical Fiber Sensors (OFS), Jeju, Korea, https://doi.org/10.1117/12.2263462, 2017.
Zaidi, F., Nannipieri, T., Soto, M. A., Signorini, A., Bolognini, G., and Di Pasquale, F.: Integrated hybrid Raman/fiber Bragg grating interrogation scheme for distributed temperature and point dynamic strain measurements, Appl. Opt. 51, 7268–7275, 2012.
- Abstract
- Fiber optical temperature sensing
- Incoherent optical frequency domain reflectometry
- Fiber Bragg grating temperature sensing
- Distributed Raman temperature sensing
- Calculation of the temperature based on the measured Raman backscattering traces
- Experimental temperature measurements
- Field test in a high-voltage environment
- Summary
- Outlook
- Data availability
- Competing interests
- Special issue statement
- Acknowledgements
- References
- Abstract
- Fiber optical temperature sensing
- Incoherent optical frequency domain reflectometry
- Fiber Bragg grating temperature sensing
- Distributed Raman temperature sensing
- Calculation of the temperature based on the measured Raman backscattering traces
- Experimental temperature measurements
- Field test in a high-voltage environment
- Summary
- Outlook
- Data availability
- Competing interests
- Special issue statement
- Acknowledgements
- References