Analysis and optimization of a cone flowmeter performance by means of a numerical and experimental approach

Differential pressure flowmeters are commonly used in industrial applications where, however, the upstream flow conditions are usually highly disturbed, caused by the presence, in the network pipe, of elbows, valves, etc. To achieve accurate flow measurements, the use of the cone meter is recommended as the flowmeter has the property to normalize the flow both upstream and downstream. In this paper, the authors present a cone flowmeter of new geometry that allows them to obtain better performance with respect to the original one; in particular, it provides a higher discharge coefficient (C_d) for a wider range of operating conditions.

1 Introduction

Accurate flow measurements are required in many industry applications. The ability to accurately and cheaply measure the flow rate has, in fact, a significant economic impact upon operating costs in control and production processes of several industries. The obstruction flowmeters are commonly used in typical industrial applications. Examples are the orifice meter, the nozzle meter, the Venturi meter, and Pitot meter. Orifice devices are widely used due to their smaller size and low cost, but their lower discharge coefficient, along with occurring inaccuracies in the measurement, due to erosion and corrosion of the plates (Shah et al., 2012), means their choice is discouraged where the measurement accuracy is important. On the other hand, the nozzle and Venturi meters present higher discharge coefficients, and, therefore, the most accurate flow rate evaluations.

The Venturi meters are, however, considerably larger, heavier, and more expensive than orifice plates. Their installation is also tougher (Miller, 1996). To obtain accurate measurements of the flow rate the flow upstream of the device must be as undisturbed as possible. Unfortunately, the piping systems do not guarantee such conditions because of the unavoidable presence of elbows, valves, junctions, and so forth (Ifft and Mikkelsen, 1993). Further, correct measurements of upstream and downstream pressures require that the obstruction device causes as low disturbances as possible on the relative pressure fields (Prabu et al., 1996; Sapra et al., 2011).

In this paper, the authors investigate the performance ensured by the cone flowmeter. In Prabu et al. (1996), an interesting study about the effect of upstream flow disturbances on the value of the cone flowmeter discharge coefficient is performed. Mainly for this reason, recently, the cone flowmeter has emerged as the most attractive choice for industrial applications, able to measure the flow rate in accurate manner, even in the presence of disturb sources (Ifft and Mikkelsen, 1993), and presenting a discharge coefficient less sensitive to the Reynolds number (Hollingshead et al., 2011). Because of its characteristic shape, the cone meter has other merits, such as higher durability and higher resistance to the abrasion, compared to other differential pressure flowmeters (Ifft and Mikkelsen, 1993).

In this paper, a cone flowmeter of new geometry is introduced, and it is able to guarantee higher performances than the original one. A numerical study is also pursued to evaluate the limits of its best working conditions. Its performances have been numerically and experimentally evaluated in terms of the discharge coefficient as a function of the flow rate and by considerations on velocity and pressure fields both upstream and downstream from the meter device. The cone meter normed by the ISO standard (5167-5:2016, 2016) is a patent of McCroMeter Inc, named V-Cone^®.

2 Cone flowmeter principle of operation

The cone is an obstruction-type flowmeter. The development of such a device arises from the challenge of improving the fluid dynamic performance usually granted by other obstruction flowmeters. Indeed, its tapered shape allows the reduction of the fluid dynamic losses due to the more favourable drag coefficient. Thus, the cone flowmeter shows average performances, which are comparable to the most expensive flowmeters, such as the nozzle flowmeter.

The principle of operation of the cone flowmeter is based on the measurement of the pressure drop upstream and downstream from the cone itself, as for all obstruction devices. The insertion of the obstacle within the flow alters the incoming velocity profile. In addition, the deviation of the streamlines around the obstacle modifies the pressure distribution upstream and downstream from the cone. In this case, the wake effect, due to the streamlines' disturbance, creates a depression zone immediately downstream from the cone base, while, in the frontal region of the cone, the streamlines are abruptly slowed down, with the following pressure increase.

The pressure drop caused by the cone insertion can be related to the mass flow rate of the fluid by means of the Bernoulli relation, valid for incompressible flows.

$$\begin{array}{}\text{(1)}& \dot{m}=Z{C}_{\mathrm{d}}E{F}_{\mathit{\alpha }}K\sqrt{\mathrm{2}\mathit{\rho }\mathrm{\Delta }p}\end{array}$$

The nomenclature is listed in Appendix A. In Eq. (1), the geometric coefficient and the cone diameter ratio are $K=\mathit{\pi }{D}^{\mathrm{2}}{\mathit{\beta }}^{\mathrm{2}}/\left(\mathrm{4}\sqrt{\mathrm{1}-{\mathit{\beta }}^{\mathrm{4}}}\right)$ and $\mathit{\beta }=\sqrt{\mathrm{1}-d^{\mathrm{2}}/D^{\mathrm{2}}}$, respectively. In Eq. (1), the term Z is the compressibility factor and takes into account any deviation from the incompressibility hypothesis (any compressibility effect can be neglected if the Mach number is less than 0.3), the term F_α includes any thermal expansion and contraction of the cone, and it has to be considered if the operating temperatures deviate from the calibration conditions.

The discharge coefficient C_d is the cone calibration factor and it can be considered a parameter indicating the performance of the device. Many investigations about the cone performance have been carried out and they are aimed at evaluating the influences of the flow conditions on the cone discharge coefficient. In Borkar et al. (2013) and Singh et al. (2006), the authors have shown that the C_d factor is quite independent of the Reynolds number for fully developed turbulent flow, and it is nearly independent of the V-Cone diameter ratio β. In addition, the overall performance of the cone is not heavily influenced by any disturbance upstream (due to elbows, throttles, valves, etc.), because it requires shorter upstream pipe lengths for the flow to get stabilized (Singh et al., 2006).

In this paper, the authors perform a series of studies, both numerical and experimental, aimed at improving the performance of a given cone flowmeter by means of the optimization of its geometry. For both shapes (the original one and the proposed modification) a series of numerical computations have been performed in order to determine the degree of influence.

3 Experimental setup

The cone flowmeter to be optimized is used to measure the fluid flow rate in a piping system feeding combustion air. The considered piping system is part of a combustion test facility owned by AC Boilers S.p.A.

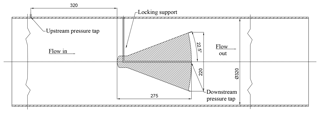
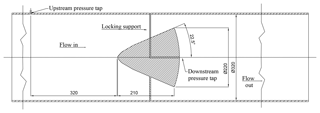
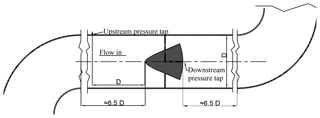
Figure 1 shows the cross-sectional drawing of the standard compliant flowmeter (hereinafter referred to as the Standard Geometry flowmeter, S-G). The cone geometry is compliant with the ISO standard (5167-5:2016, 2016). The upstream and downstream pressure taps' locations are sketched in the same figure. The static upstream pressure tap is located at 1D upstream of the cone itself; the other static pressure tap is placed at the cone base by means of a drilling hole along the cone axis. Figures 2 and 3 show, respectively, the cross-sectional drawing and the picture of the proposed cone flowmeter. Figure 4 shows a schematic view of the facility equipping the tested cone. The pipe inner diameter, D, is 320 mm. Both flowmeters have β=0.73 and an angle equal to 45^∘. An undisturbed pipe length of 6.5 D upstream and downstream from the cone is guaranteed in order to ensure a fully developed flow condition in the proximity of both cones (Fig. 5). The mass fluid flow rate range in the usual operating conditions of the plant is 0.5–1.8 kg s⁻¹, with a global Reynolds number range of 111 180–400 245 and a local Reynolds number range (in the cone proximity) of 65 884–237 182. The differential static pressure (corresponding to the pressure drop induced by the flowmeter) is measured by means of two differential pressure transducers (Rosemount^™ type) with an uncertainty of ±0.075 % of the reading. In addition, the cone is calibrated against a turbine flowmeter (Elster^® Q75) with a declared uncertainty of ±1.5 % of the reading value. The S-G flowmeter has a claimed discharge coefficient C_d=0.80 with an extended uncertainty which is not less than ±5 % (95 % confidence interval) under the following conditions, according to the ISO standard (5167-5:2016, 2016):

• global Reynolds number, Re_D, ranging from 8×10⁴ up to 12×10⁶;

• pipe diameter such that $\mathrm{0.45}\le \mathit{\beta }\le \mathrm{0.75}$.

The tests involving the proposed cone have been performed with air at standard conditions. The acquisitions of differential pressure values and the mass flow rates have been made once the reading, in both cases, has reached stability. The comparison between the features characterizing both cones has been performed by means of numerical simulations. In addition, the verification of the performance of the introduced P-G cone has been made by means of a series of measurements whose description is reported later.

Figure 1 Schematic view of the original cone flowmeter, with the upstream and downstream pressure taps.

Figure 2 Schematic view of the proposed modified cone flowmeter.

Figure 3 Proposed cone flowmeter.

Figure 4 Piping system equipping the tested flowmeters.

Figure 5 Schematic view of the installed P-G cone.

4 Numerical simulations

In this paper, the evaluation of the features of both geometries has been primarily accomplished by means of a series of numerical simulations based on CFD (computational fluid dynamics) modelling. The target of the simulations is to establish the extent of the influence of the inlet fluid flow rate and the influence of the cone diameter ratio β on the discharge coefficient and the improvements brought by the new geometry.

4.1 Pre-analysis

The same strategy and criteria have been adopted for the numerical modelling of both systems. The simulation procedure is based on the solution of the governing equations, continuum and momentum, with the adoption of an appropriate turbulence model aimed at providing the closure constraints to the RANS (Reynolds-averaged Navier–Stokes) equations. The RANS equations describe entirely the flow behaviour in steady and incompressible conditions. In this paper, the authors use the RNG (Re-Normalization Group) k–ϵ turbulence model (Markatos, 1986; Yakhot and Orszag, 1986). This model, coupled to an adequate near-wall treatment function, describes efficiently the fluid motion for a wide range of industrial applications involving flow in pipes (Singh et al., 2009; Shah et al., 2012).

4.2 Governing equations and adopted mesh description

The CFD provides the numerical solution of the governing equations of motion and describe the flow behaviour. The adopted mathematical model shall consider the flow general condition (incompressible or compressible) and the known boundary conditions.

The mathematical model is based on the mass, momentum, and energy conservation equations (for compressible flows). For incompressible flows, only the mass and momentum conservation equations are considered. In addition, for turbulent flows, the governing equations shall consider the velocity fluctuations around the mean value. In this case, the Reynolds decompositions of both flow pressure and velocity allow us to give approximate time-averaged solutions to the governing equations (mainly mass and momentum for incompressible flows).

In steady and incompressible conditions without any body forces, the time-averaged governing equations are provided in vector form.

$$\begin{array}{}\text{(2)}& {\displaystyle }& {\displaystyle }\mathrm{\nabla }\cdot \mathit{U}=\mathrm{0}\text{(3)}& {\displaystyle }& {\displaystyle }\mathrm{\nabla }\cdot (\mathit{\rho }\mathit{U}\cdot \mathit{U})=-\mathrm{\nabla }\cdot P+\mathrm{\nabla }\cdot \mathit{T}\end{array}$$

Equation (2) is the time-averaged mass conservation, Eq. (3) the RANS. In Eq. (3), the term T is the overall stress tensor, provided by Eq. (4).

$$\begin{array}{}\text{(4)}& \mathit{T}={\mathit{\mu }}_{\mathrm{eff}}[\mathrm{\nabla }\cdot \mathit{U}+(\mathrm{\nabla }\cdot \mathit{U}{)}^T-\mathrm{2}{\mathit{\mu }}_{\mathrm{eff}}\mathrm{\nabla }\cdot \mathit{U}\mathit{I}]\end{array}$$

In Eq. (4), the term μ_eff is the total effective dynamic viscosity, provided by the following relation.

$$\begin{array}{}\text{(5)}& {\mathit{\mu }}_{\mathrm{eff}}=\mathit{\mu }+{\mathit{\mu }}_t=\mathit{\mu }+\mathit{\rho }{\displaystyle \frac{C_{\mathit{\mu }}{k}^{\mathrm{2}}}{\mathit{ϵ}}}\end{array}$$

In Eq. (5), the second term is a fictitious contribution due to the turbulence. The term C_μ is a constant. The introduction of the Reynolds stresses in Eq. (4) requires two additional transport equations for variables k and ϵ. The equations are derived from the RANS equations by means of the re-normalization group theory (Yakhot and Orszag, 1986).

$$\begin{array}{}\text{(6)}& {\displaystyle }\mathrm{\nabla }\cdot (\mathit{U}\cdot \mathit{\rho }k)=\mathrm{\nabla }\cdot \left[{\mathit{\alpha }}_k{\mathit{\mu }}_{\mathrm{eff}}\mathrm{\nabla }\cdot k\right]+G_k-\mathit{\rho }\mathit{ϵ}\text{(7)}& {\displaystyle }\begin{array}{rl}\mathrm{\nabla }\cdot (\mathit{U}\cdot \mathit{\rho }\mathit{ϵ})& =\mathrm{\nabla }\cdot \left[{\mathit{\alpha }}_{\mathit{ϵ}}{\mathit{\mu }}_{\mathrm{eff}}\mathrm{\nabla }\cdot \mathit{ϵ}\right]+C_{{\mathit{ϵ}}_{\mathrm{1}}}{\displaystyle \frac{\mathit{ϵ}}{k}}{G}_k+C_{{\mathit{ϵ}}_{\mathrm{2}}}{\displaystyle \frac{{\mathit{ϵ}}^{\mathrm{2}}}{k}}{G}_k\\ & -\mathit{\rho }\mathit{ϵ}-R\end{array}\end{array}$$

In Eq. (7), the term G_k is the generation of turbulent kinetic energy due to the mean velocity gradient (Launder and Spalding, 1974), and it is calculated as G_k=μ_tS². S is the mean rate of the shear stress tensor. The constants in Eqs. (6) and (7) are the standard values available in the literature, according to Yakhot and Orszag (1986): C_μ=0.0845, $C_{{\mathit{ϵ}}_{\mathrm{1}}}=\mathrm{1.42}$, $C_{{\mathit{ϵ}}_{\mathrm{2}}}=\mathrm{1.68}$, and ${\mathit{\alpha }}_k={\mathit{\alpha }}_{\mathit{ϵ}}=\mathrm{0.7179}$.

The governing equations are solved numerically using the finite-volume approach. According to this method, the entire geometric domain is divided into a finite number of cells. The flow simulations carried out for both geometries have been performed by means of the Ansys Fluent CFD commercial code (ANSYS, 2013). The principle of operation of the solver is based on cell-centred finite-volume approach. Therefore, an appropriate geometry discretization is crucial in order to get appropriate and accurate simulation results. Finer grids lead to more accurate flow evaluations, but they are computationally expensive. In the presented case studies, 2-D axisymmetric domains for both geometries are considered along with an unstructured mesh of the flow domain. In order to get more refined and accurate results in the boundary layer of both pipe and flowmeter walls, an appropriate inflation strategy has been adopted.

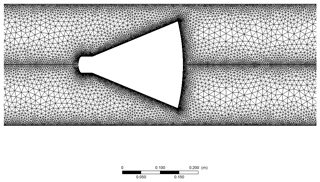
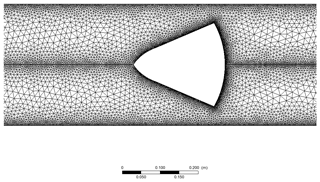
Figure 6 shows the adopted mesh grid for the standard cone, and Fig. 7 illustrates the mesh of the proposed cone.

Figure 6 Unstructured mesh for the S-G cone.

Figure 7 Unstructured mesh for the P-G cone flowmeter.

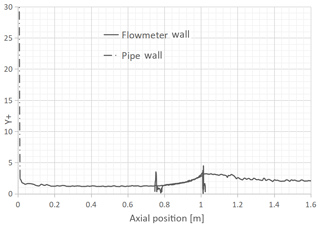
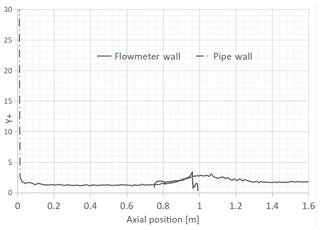
The upstream pipe length is 3-D in both cases and the downstream pipe length has been chosen in order to ensure that the flow conditions, in the flowmeter proximity, are uninfluenced by the boundary condition at the pipe exit. Additionally, the adopted inflation strategy close to the flowmeter and wall boundary layers ensures that at least one grid layer is within the viscous sublayer ($y^{+}\approx \mathrm{1}$, still $y^{+}<\mathrm{5}$, as shown in Figs. 8 and 9). In this condition, it is possible to implement enhanced near-wall treatment functions in order to accurately resolve the flow condition in the boundary layer regions.

Figure 8 y⁺ trend in the flowmeter and pipe walls' proximity, SG cone.

Figure 9 y⁺ trend in the flowmeter and pipe walls' proximity, PG cone.

For both geometries, unstructured triangular meshes have been used in all the simulations. In the analysed cases, the unstructured meshing approach, adequately refined at the boundary layers, implies optimized setup time and computational effort. In order to evaluate the suitability of the adopted meshing schemes, further attention has been dedicated to the analysis of the mesh goodness metrics. Checking the mesh quality plays an important role in the assessment of the stability and the accuracy of the numerical computations. The most relevant goodness indicators are the orthogonal quality, the aspect ratio (as a measure of the cell stretching), and the skewness of each cell (a measure of how closely ideal a cell is). The implemented mesh schemes are characterized by cells with orthogonal quality and aspect ratios very close to 1 and a skewness never larger than 0.25. The solution scheme implemented in the CFD solver is based on the pressure–velocity coupling using the SIMPLE scheme (ANSYS, 2013). The gradients of pressure and velocity fields have been discretized according to the Green–Gauss node-based evaluation (which is claimed to be more stable for triangle-based meshes). The adopted pressure interpolation strategy is based on the second-order scheme, and the spatial discretization of momentum, turbulent kinetic energy, and turbulent dissipation rate are based on the second-order upwind scheme (ANSYS, 2013).

4.3 Boundary conditions

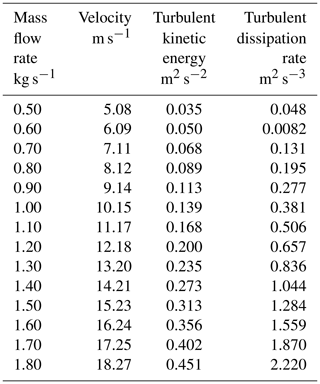
For all the simulations involving the two geometries, some specific boundary conditions have been set. The inlet mass flow rate (air at standard conditions) is among those conditions. Since the main purpose is to evaluate the discharge performance of both flowmeters, it has been considered an inlet mass flow rate ranging from 0.5 kg s⁻¹ up to 1.8 kg s⁻¹ (corresponding to the operating flow range of the piping system). An operating relative pressure of 0 Pa has been set at the outlet and the no-slip condition for the walls has been considered. The first parameter to consider for a complete definition of the flow properties, at the inlet, is the turbulent intensity. For a fully developed flow, it can be estimated by means of Eq. (8) (Pope et al., 2000).

$$\begin{array}{}\text{(8)}& I={\displaystyle \frac{u^{\prime }}{U}}=\mathrm{0.16}{\left(R{e}_{\mathrm{D}}\right)}^{\mathrm{1}/\mathrm{8}}\end{array}$$

In Eq. (8), the term u^′ indicates the fluctuant velocity component and U the average component. According to the set inlet mass flow rate, the term I varies between 3 % and 4 %. The relationship between turbulent kinetic energy, k, and the turbulent intensity is

$$\begin{array}{}\text{(9)}& k={\displaystyle \frac{\mathrm{3}}{\mathrm{2}}}(UI{)}^{\mathrm{2}}.\end{array}$$

The turbulent dissipation rate is estimable from the turbulent length scale, l, according to Eq. (10).

$$\begin{array}{}\text{(10)}& \mathit{ϵ}=C_{\mathit{\mu }}^{\frac{\mathrm{3}}{\mathrm{4}}}{\displaystyle \frac{k^{\frac{\mathrm{3}}{\mathrm{2}}}}{l}}\end{array}$$

In Eq. (10), the term l is the turbulent length scale, which is 0.07 D for fully developed flows in a pipe. The term C_μ is a constant (Launder and Spalding, 1974). The boundary conditions at the pipe inlet are summarized in Table 1.

Table 1 Inlet boundary conditions for simulations relative to both cones.

4.4 Verification and validation of the CFD results

The verification procedure determines whether the implemented mathematical model has been solved correctly. The task can be accomplished by checking the consistency of the obtained results with the mathematical model, the level of numerical errors (due to the discretization and linearization of the governing equations), and by means of a comparison with hand calculations (if those are easily available). The validation procedure, on the other hand, looks at whether the used mathematical model is correct and, therefore, consistent with the physical problem under study. The task is carried out by checking the simulation results against experimental data. In this paper, the verification procedure is performed through several steps. The preliminary and most basic step to implement consists of a series of sanity checks on the pressure and velocity contours. The following step is a check whether the CFD solution honours the boundary conditions and the physical principles in the mathematical model (i.e. conservation of mass, momentum, and energy in the analysed domain). The check of mass and momentum conservation in the whole domain is straightforward and, therefore, omitted in the paper. An appropriate subsection is dedicated to the energy balance. A further operation to perform (in the verification procedure framework) is the assessment of the acceptability of the linearization error and the discretization error. The first is implemented by checking the residuals and the convergence rate of the solutions of governing equations. In addition, a further check of the convergence rate of the drag coefficient is performed. The check of the discretization error is performed by means of the comparison of the solutions obtained from the mesh refinement.

4.4.1 Energy balance check

For a steady incompressible flow, the energy conservation equation is provided by Eq. (11).

$$\begin{array}{}\text{(11)}& {\displaystyle \frac{p_{\mathrm{in}}}{\mathit{\rho }}}+{\displaystyle \frac{U_{\mathrm{in}}^{\mathrm{2}}}{\mathrm{2}}}={\displaystyle \frac{p_{\mathrm{out}}}{\mathit{\rho }}}+{\displaystyle \frac{U_{\mathrm{out}}^{\mathrm{2}}}{\mathrm{2}}}+l_w\end{array}$$

Equation (11), valid for horizontal pipes, is the mechanical energy balance, in integral form, between inlet and outlet sections. The term l_w represents the dissipation of energy, which is mainly due to viscous effects. For turbulent flows, the energy dissipation can be estimated by considering the turbulence characteristics, such as non-linearity, vorticity diffusivity, and dissipative attitude of the vortices at smaller scales. Indeed, the kinetic energy cascades down from larger to smaller eddy scales. At very smaller scales, the energy of eddies dissipates into heat, and such a phenomenon is due to viscous forces. The turbulent energy dissipation rate, ϵ, is the physical quantity for the estimation of the amount of energy lost by the viscous forces in the turbulent flow. Therefore, the term l_w can be estimated by means of Eq. (12).

$$\begin{array}{}\text{(12)}& {\dot{l}}_{w,\mathit{ϵ}}=\mathit{\rho }\int \mathit{ϵ}\mathrm{d}V\end{array}$$

Equation (12) is valid for incompressible flows, and it indicates the integral (over the whole flow domain) of the turbulent kinetic energy dissipation rate. In addition, the energy dissipation rate ${\dot{l}}_{w,B}$ can be estimated by means of a time derivation of Eq. (11).

$$\begin{array}{}\text{(13)}& {\dot{l}}_{w,B}=\dot{m}{\displaystyle \frac{\mathrm{\Delta }{p}_{\mathrm{L}}}{\mathit{\rho }}}\end{array}$$

In Eqs. (12) and 13, ${\dot{l}}_{w,B}$ is the time derivative of l_w and Δp_L is the permanent pressure loss between pipe inlet and outlet. For turbulent incompressible flows, the energy balance check can be performed by comparing the energy dissipation rate computed by means of Eqs. (12) and (13). In this subsection, the data of the energy balance check pertaining to some cases are reported, for brevity reasons.

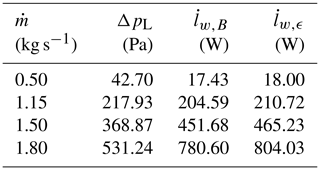
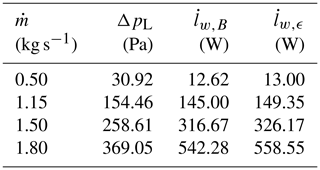
Table 2 shows the energy balance check for some simulations relative to the standard geometry cone. In all cases, there exists a significant agreement (within 3 %) between the energy dissipation rate computed by means of the Bernoulli equation, ${\dot{l}}_{w,B}$, and the dissipation rate computed by means of the volume integration of ϵ, ${\dot{l}}_{w,\mathit{ϵ}}$.

Table 2 Energy balance check for simulations relative to the standard geometry cone.

Table 3 contains the data relative to the energy balance check of some simulations relative to the proposed cone. Even in this case, the accordance between ${\dot{l}}_{w,B}$ and ${\dot{l}}_{w,\mathit{ϵ}}$ is approximately within 3 %. An analysis of Tables 2 and 3 points out that the proposed cone ensures more favourable power requirements.

Table 3 Energy balance check for simulations relative to the proposed geometry cone.

4.4.2 Mesh refinement analysis

The mesh refinement analysis allows us to check the level of discretization error.

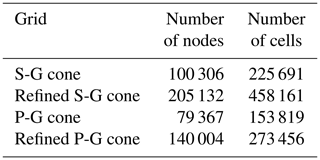
Table 4 lists the number of elements and nodes relative to the computational grids of both flowmeters (considered as 2-D axisymmetric domains). In this section, for brevity reasons, only the comparison results relative to the simulations with an inlet mass flow rate of 1.8 kg s⁻¹ are considered.

Table 4 Mesh metrics for both geometries.

Figure 10 shows the contour plot of the difference of the solutions of the axial velocity from the refined and original meshes for the standard cone. The contour plot is relative to the simulations with an inlet mass flow rate of 1.8 kg s⁻¹. The maximum difference is about 3 %. Figure 11 shows the contour plot of the difference of pressures from both grids relative to the standard cone. For the pressure, the maximum difference is less than 1 %. The very limited difference of the velocity and pressure solutions obtained by a mesh refinement is a further step to the verification of the CFD simulations. Analogous considerations are reported for the simulations carried out on the proposed cone flowmeter.

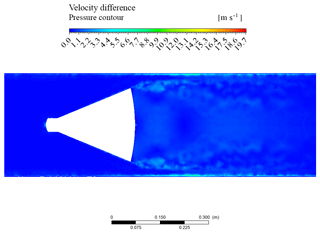
Figure 10 Contour plot of the axial velocity difference between the original mesh and the refined one, S-G V-Cone.

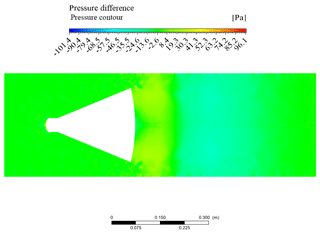
Figure 11 Contour plot of the pressure difference between the original mesh and the refined one, S-G V-Cone.

Figures 12 and 13 show the mesh refinement influence on the CFD results relative to the proposed geometry flowmeter. In this case, the maximum discrepancy between the solutions of the axial velocity magnitude from both tested computational grids is about 3 %. For the pressure solutions, the maximum difference is about 0.5 %. Even for the simulations carried out on the proposed flowmeter geometry, the verification of the CFD simulations can be considered achieved.

Figure 12 Contour plot of the axial velocity difference between the original mesh and the refined one, proposed cone.

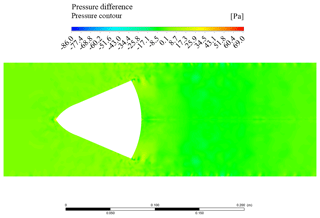
Figure 13 Contour plot of the pressure difference between the original mesh and the refined one, proposed cone.

The validation of the CFD simulations against experimental data will be later discussed only for the proposed flowmeter geometry, because experimental results could not have been obtained for the standard device due to the instability of the flow caused by its unexpected fluctuation. Such a phenomenon has not occurred for the P-G cone, whose installation is ensured by locking supports in the central area of the lateral surface of the cone at 180^∘ from one another, as shown in Fig. 2.

4.5 Flow pattern analysis

Several simulations have been performed in order to evaluate the performance of the S-G cone with different inlet mass flow rates. In this section, only the solutions obtained with a flow rate of 1.8 kg s⁻¹ are considered.

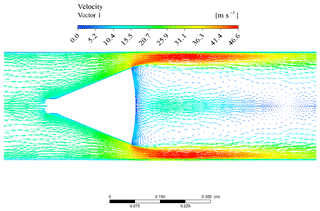
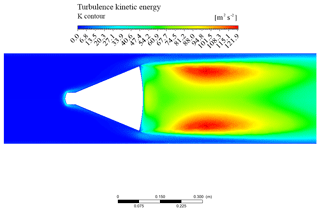
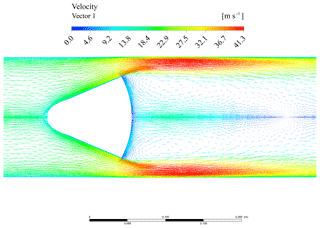
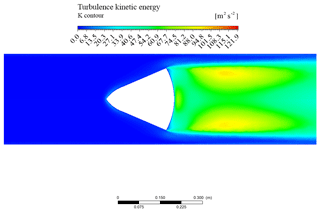
Figure 14 shows the velocity vector map. The flow is approximately undisturbed upstream of the cone itself. Then, narrowing the cross section (due to the presence of the obstacle), the flow accelerates. The separation of the boundary layer on the rear side of the cone takes place, forming a free-flowing jet downstream. Turbulent wakes and recirculation regions can be observed just downstream from the flowmeter. Figure 15 shows the turbulent kinetic energy contour plot. The largest values are located downstream, where the largest velocity gradients occur, due to the flow separation, and re-organized in recirculating zones.

Figure 14 Velocity vector map, S-G flowmeter.

Figure 15 K contour plot, S-G V-Cone.

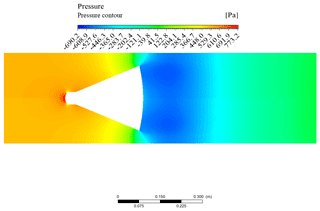
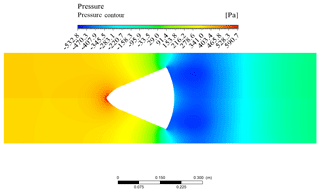
Figure 16 shows the pressure contour plot. As the flow accelerates, the pressure decreases. The pressure drop across the cone is particularly evident. Downstream from the maximum pressure drop, the decrease in flow kinetic energy causes an increase in the static pressure.

Figure 16 Relative static pressure contour plot.

For the proposed cone geometry, the results of the simulations carried out with an inlet mass flow rate of 1.8 kg s⁻¹ are going to be reported.

In this case, it is possible to make the same considerations relative to the standard cone. In addition, a comparison of Figs. 15 and  18 indicates that the amount of the turbulent kinetic energy is dramatically reduced in the P-G cone. Indeed, the S-G geometry of the maximum value of the turbulent kinetic energy is k_MAX=121.8 J kg⁻¹. For the P-G geometry, k_MAX=94.8 J kg⁻¹, resulting in a reduction of the turbulent kinetic energy of 13 %. Additionally, the extent of the dissipation rate of the turbulent kinetic energy is significantly reduced by 73 %.

Figure 17 Velocity vector map, proposed flowmeter.

Figure 18 K contour plot, S-G V-Cone.

Therefore, the introduced flowmeter geometry introduces fewer head losses (Eqs. 10, 12, and 13).

The whole fluid flow pattern, through both flowmeters, has been analysed at different mass fluid flow rates, and, therefore, at different Reynolds numbers. Figures 14 and 17 suggest that, for both cones, a pair of contra-rotating vortices in the recirculation zone, just downstream from the obstruction, take place. The downstream extension of those vortices mainly depends on the obstruction geometry and the Reynolds number. At higher Re the axial extension of the downstream vortices increases. At any Re, the proposed geometry ensures slightly less extended recirculation zones.

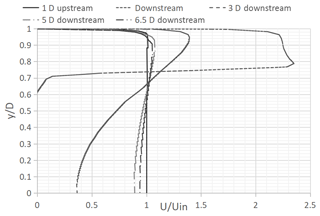
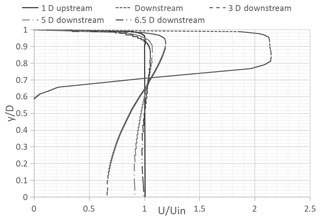
Figure 20 shows the evolution of the velocity profile at different axial locations relative to the standard cone geometry. Figure 21 shows several velocity profiles (at the same locations as the S-G cone) observed in the proposed cone geometry. In both cases, the recirculation region extends up to approximately 3-D, with an extended wake effect up to approximately 5-D. Both figures refer to an inlet mass flow rate of 1.8 kg s⁻¹.

Figure 19 Relative static pressure contour plot.

Figure 20 Velocity profiles at different axial positions, S-G cone.

Figure 21 Velocity profiles at different axial positions, P-G cone.

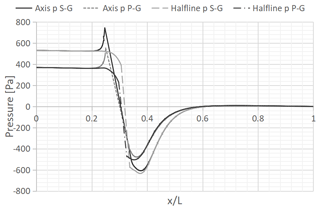
Figure 22 shows the flow pressure, along the pipe axial direction, for both flowmeters. The considered mass fluid flow rate is 1.8 kg s⁻¹.

Figure 22 Relative pressure along the axial direction.

It can be noted that the proposed cone geometry ensures reduced pressure drops through the obstacle. Additionally, just upstream of both cones, the static pressure increases. Indeed, the presence of the obstruction within the pipe reduces the effective section. The converging section imposes a back pressure on the upstream, forcing the flow streamlines in the proximity of the pipe centreline to slow down and divert from the centre. The remarkable pressure drop, just downstream from the cone, is due to the flow acceleration through the annular section. Figure 22 suggests that for any mass fluid flow rate, the pressure drop experienced by the proposed cone geometry is lower.

5 Results

In this section, the authors present a series of results about the evaluation of the performance ensured by the cones, with the purpose of pointing out the enhancements provided by the improved geometry.

5.1 Discharge coefficient

The discharge coefficient has been calculated by means of Eq. (1) using the data obtained from the CFD simulations and the experimental tests (only available for the proposed cone).

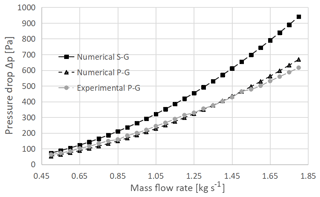
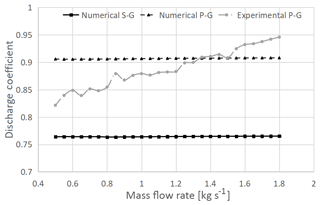
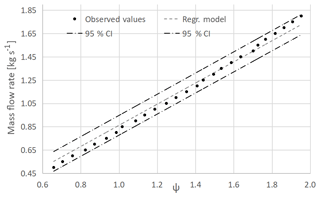
Figure 23 shows the pressure drop through the flowmeters, as a function of the inlet mass flow rate (in the range 0.5–1.8 kg s⁻¹). The pressure drop is evaluated at the two pressure taps (upstream and downstream from the cone) whose location has been reported previously. In addition, for the proposed cone, the experimental data have been presented. An excellent agreement between the numerical and experimental data for the introduced cone can be ascertained. Such a result corroborates the validation of the performed CFD simulations. Figure 24 shows the discharge coefficient, deducted from numerical simulations for the standard cone and from simulation and experimental data for the proposed cone. The introduced geometry guarantees the best discharge coefficient as the mass flow rate changes. The numerical simulations point out a constant C_d coefficient. This results are coherent with the those available in the literature (Singh et al., 2006, 2009; Shah et al., 2012; Zhang and Dong, 2009).

Figure 23 Pressure drop due to the cone for both geometries.

Figure 24 C_d coefficient against inlet mass flow rate.

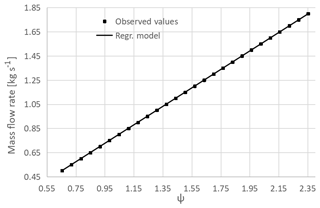
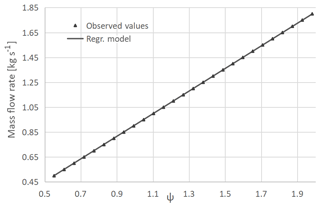
Figures 25–27 illustrate the results of the linear least squares fit of the linearized version of Eq. (1), for the standard cone and the proposed one (based on CFD and experimental data) (Eq. 14). The Ψ parameter is provided by Eq. (15).

$$\begin{array}{}\text{(14)}& {\displaystyle }& {\displaystyle }\dot{m}=C_{\mathrm{D}}\cdot \mathrm{\Psi }\text{(15)}& {\displaystyle }& {\displaystyle }\mathrm{\Psi }=ZE{F}_{\mathit{\alpha }}K\sqrt{\mathrm{2}\mathit{\rho }\mathrm{\Delta }p}\end{array}$$

Figure 25 Least squares regression fit, S-G cone.

Figure 26 Least squares fit of CFD data, proposed cone.

Figure 27 Least squares fit of experimental data, P-G cone.

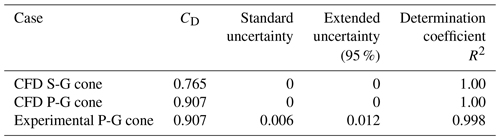
Table 5 lists the computed C_D, along with the standard and extended uncertainties, and the fit determination coefficient R² (Figliola and Beasley, 2010).

Table 5 Linear fit parameters.

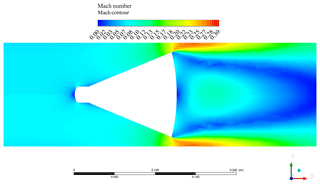
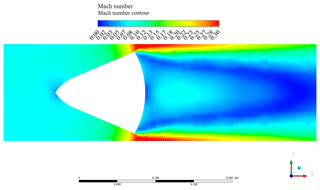
It is possible to point out the excellent agreement of the values, computed from the CFD simulations, with an adopted linear model. Additionally, it is possible to deduce the excellent degree of concordance between the CFD simulations performed on the proposed cone and the relative experimental data. Further, in this study, the authors analyse the performance ensured by both flowmeters with the cone diameter ratio β. With this aim, additional CFD computations have been performed, simulating flow conditions characterized by a global Re ranging from 90 000 to 500 000 and a local Re from 60 000 up to 275 000. For both flowmeters, the operating range of β has been calculated. The lower bound is due to the compressibility effects (no longer negligible for Mach numbers larger than 0.3), which compromise the validity of Eq. (1). The upper limit is due to the need to ensure a detectable pressure drop through the obstruction. Figure 28 represents the results of the study of how the flow compressibility effects become more influential as the pipe inner diameter decreases. The Mach number distribution relative to the standard geometry cone in a pipe of 140 mm diameter, corresponding to a cone diameter ratio of 0.620, is shown. In this condition, the flow locally reaches a Mach number approximately equal to 0.30. Further pipe diameter reductions imply more significant compressibility effects, making the estimation of the discharge coefficient based on Eq. (1) ineffective.

Figure 28 Mach number contour map, S-G V-Cone, β≈0.620.

Figure 29 is the contour plot of the Mach number relative to proposed geometry, for β≈0.533. Also, in this case, the flow locally reaches Mach 0.30. The comparison between Figs. 28 and 29 points out that the proposed geometry offers a larger operating range of β, where it is possible to infer the mass fluid flow rate, by means of Eq. (1).

Figure 29 Mach number contour map, P-G V-Cone, β≈0.533.

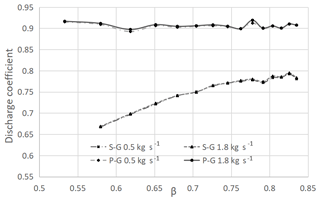
Figure 30 shows the influence of the cone diameter ratio on the discharge coefficient at two different mass flow rates (0.5 and 1.8 kg s⁻¹). First, it can be confirmed that the discharge coefficient remains quite unaffected by the inlet mass flow rate (as the flow is globally turbulent).

Figure 30 Discharge coefficient vs. β.

Figure 31 Permanent pressure loss percentage against mass flow rate for both cones, β=0.726.

In addition, the C_D of the standard geometry is influenced by the β ratio (or, equivalently, by pipe diameter), and it increases up to the asymptotic value of 0.792. On the other hand, the proposed cone geometry exhibits a C_D coefficient unaffected by β. The C_D variability should discourage the use of the standard cone in applications characterized by β different from the calibration condition.

5.2 Permanent pressure loss analysis

In this section, the authors perform a detailed analysis of the permanent pressure losses induced by both cone geometries. The permanent pressure losses have been defined as the percentage of the pressure drop (measured at the static pressure taps) induced by the obstruction (Figliola and Beasley, 2010; Miller, 1996). The insertion of the flowmeter within the flow increases the fluid dynamic loss (usually due to the friction effect at the wall) because of the turbulent kinetic energy dissipation occurring just beyond the flowmeter, as has been pointed out in the energy balance check section.

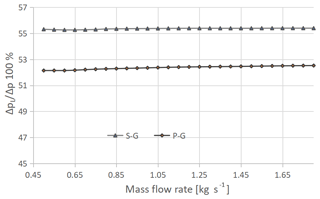
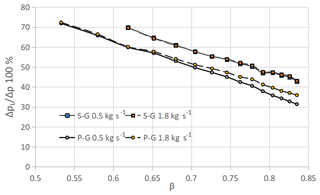
Figure 31 illustrates the permanent pressure losses, for both cones, in the operating mass flow rate range, with β=0.726. The proposed geometry ensures less permanent pressure drops, as has been pointed out in the energy balance check section (Tables 2 and 3). In addition, it can be observed that the increase in Δp_L is of the same magnitude as of Δp through the cone, making their ratio constant with the flow rate. Figure 32 reports the permanent pressure losses, at two different mass flow rates, against the cone diameter ratio. It can be pointed out that the fluid dynamic losses decrease with β. Indeed, the relative increase in pipe cross section in the cone insertion region decreases the effects of flow acceleration and pressure drop, resulting in less fluid dynamic losses. In addition, as β increases, the downstream flow diffusion is more efficient, resulting in more limited permanent pressure losses.

Figure 32 Permanent pressure loss percentage against β for both cones.

6 Conclusions

The aim of the presented paper is to introduce a cone flowmeter characterized by an optimized geometry. In order to assess the enhancements brought by the introduced flowmeter, a series of comparative analyses with a standard cone have been performed. These studies are based on CFD simulations and experimental measurements (available for the proposed cone only) performed on a test facility. The following considerations can be made because of the carried-out evaluations.

1. The proposed geometry introduces less downstream turbulence. Consequently, the turbulent dissipation rate, granted by the modified geometry, is more favourable. Such a behaviour implies less permanent pressure loss and a prompter static pressure recovery downstream.

2. The presented V-Cone exhibits fewer pressure drops, between the measuring pressure taps, for any tested mass flow rate (Fig. 23).

3. The discharge coefficient is quite independent of the inlet flow conditions, as the flow remains globally turbulent and, at inlet, fully developed (Fig. 24).

4. The discharge coefficient, ensured by the introduced geometry, is 15.7 % larger for the tested conditions characterized by a cone diameter ratio of 0.726 (Figs. 24 and 30).

5. The influence of cone diameter ratio on the discharge coefficient has been analysed. The standard geometry exhibits a decreasing trend, as β approaches lower values. However, the proposed cone performance is unaffected by any variation of β in the studied range (Fig. 30), with no need for recalibration in case of cone insertion in a pipe with a different inner diameter.

6. The introduced flowmeter ensures less permanent pressure drops, due to the lower turbulence induced by the characteristic geometry.

Appendix A: Nomenclature

Symbol	Description (physical unit)
$\dot{m}$	Mass flow rate (kg s−1)
Cd	Discharge coefficient
D	Pipe inner diameter (m)
d	Cone flowmeter base diameter (m)
ρ	Fluid density (kg m−3)
Δp	Pressure drop through the cone flowmeter (Pa)
ΔpL	Permanent pressure loss (Pa)
μ	Molecular dynamic viscosity (Pa s−1)
β	Cone diameter ratio
K	Flow geometric coefficient
E	Flow compressibility factor
Fα	Material thermal expansion factor
$\mathit{u}=\mathit{U}+{\mathit{u}}^{\prime }$	Reynolds decomposition of flow velocity vector
$p=P+p^{\prime }$	Reynolds decomposition of flow pressure
k	Turbulent kinetic energy (m2 s−2) or (J kg−1)
ϵ	Dissipation rate of turbulent kinetic energy (m2 s−3) or (W kg−1)
r	Radial coordinate
z	Axial coordinate