the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
High-temperature stable piezoelectric transducers using epitaxially grown electrodes
Hendrik Wulfmeier
René Feder
Li Zhao
Holger Fritze
Piezoelectric resonators are of great importance for application in high-precision transducers. However, at elevated temperatures, the degradation of commonly used metal electrodes may affect the performance of oxide electrodes of piezoelectric transducers; with sufficiently high electrical conductivity they are expected to overcome this deficit. In the latter case, the stable operation of piezoelectric transducers could be further enhanced if the resonator and electrodes would consist of identical or at least very similar materials; thus, nearly monolithic resonators are created.
The present work focuses on two major aspects: the growth of high-quality langasite (La3Ga5SiO14; LGS) and doped LGS thin-film electrode layers by pulsed laser ablation and the characterization of the developed resonator devices. To obtain epitaxial films of the correct stoichiometry, the deposition on heated substrates is performed in oxygen atmosphere in the range from 10−3 to 10 Pa. Another requirement for adjusting the stoichiometry is an increased Ga content in the sputter targets with respect to LGS to account for Ga evaporation during film deposition. Additional doping with Sr increases the electrode film conductivity; thus combined with the use of low-conductivity single-crystalline catangasite (Ca3TaGa3Si2O14; CTGS) substrates the ratio between the electrical conductivities of the substrate and the film is increased, enabling the preparation of nearly monolithic resonators. The properties of these nearly monolithic resonators are characterized in the temperature range of 600 to 1000 ∘C and compared to those of CTGS resonator blanks without electrodes. Particular attention is paid to the reproducibility of resonator properties, the electrode orientation and the quality factor. The created nearly monolithic resonator demonstrates stable operation in the temperature range from 600 to 1000 ∘C.
- Article
(3126 KB) - Full-text XML
- BibTeX
- EndNote
Transducers based on piezoelectric materials are widely used in scientific and industrial devices, in particular, in gas, gravimetric or calorimetric transducers. Operation temperatures above 500 ∘C are of particular interest as the transducer signals enable efficiency improvement of e.g. high-temperature energy conversion processes (Yu et al., 2011; Tuller and Fritze, 2002; Seh et al., 2004; Thiele and Pereira da Chunha, 2006; Wulfmeier et al., 2015; Schröder et al., 2018). Here, often bulk-acoustic-wave (BAW) transducers based on high-temperature stable quartz-like crystals (in particular of the langasite family) are chosen. For example, stoichiometric langasite (La3Ga5SiO14; LGS) and catangasite (Ca3TaGa3Si2O14; CTGS) are piezoelectrically excitable up to their melting point of 1473 and 1350 ∘C, respectively (Shimamura et al., 1996; Fritze et al., 2006; Suhak et al., 2016). Furthermore, they are stable down to oxygen partial pressures of bar at 600 ∘C and 10−14 bar at 1100 ∘C (Fritze, 2010; Schulz and Fritze, 2008).
A main origin of transducer failure or degradation is, in general, neither the transducer material itself nor the active film for e.g. the detection of gas species. The transducer components showing dominating degradation are the thin-film metallic electrodes upon these extreme conditions. An option to reduce degradation is the deposition of protective oxide films (Richter et al., 2011). However, it is elaborate and of limited benefit, and other approaches such as the creation of nearly monolithic electrodes as presented subsequently are desirable. Thereby, thin-film electrodes offer the advantage of the least possible impact on resonance properties.
1.1 State of the art: electrodes for high-temperature transducers
As electrodes for active devices must have a high electric conductivity, metal electrodes are commonly applied. They are sufficiently stable and reliable at low and medium temperatures. To enhance the durability of the device at high temperatures and under different atmospheres, typically, expensive noble metals like platinum, rhodium, iridium or their alloys are preferred. A typical degradation mechanism of these metal thin films are oxidization, agglomeration or evaporation (Firebaugh et al., 1998). Thin-film platinum electrodes (of only a few hundred nanometres thickness) are operable at temperatures up to e.g. 900 ∘C (Richter et al., 2013; Wulfmeier et al., 2013, 2016). In recent decades great efforts have been made to stabilize those electrodes. One obvious approach to extend their operational limits is to increase the electrode thickness. In Suhak et al. (2016) a remarkable long-term stability for Pt-electroded CTGS resonators operating at 1000 ∘C is shown. To achieve this, the mesh-printed Pt electrodes of >5 µm thickness are used. This results not only in improved temperature stability but also in a significantly increased mass of the electrode films. However, the major drawback of this thick-film approach is a decreased resonator quality factor and, therefore, decreased mass resolution. Further, thick noble-metal films increase the production costs. Another approach to gain high-temperature stability is to cover the electrodes with a protective film (Kreider and Gillen, 2000; Gadkari et al., 2005; Richter et al., 2011). The challenge in this field is to find protective films that are stable against heat and varying atmospheres and not reactive with the electrode film at the same time. In this regard, promising results are achieved with alumina, zirconia or magnesia films. However, the major drawbacks, i.e. the additional mass on the transducer as well as the higher complexity of these transducers, remain.
The oxide-based thin-film electrodes would solve many of these problems, especially since their thermal expansion coefficients and lattice constants would match those of the transducer material underneath (Sauerwald et al., 2011). Another advantage of oxide electrodes with respect to metals is their higher stiffness that does not decrease significantly with increasing temperature. As the stiffness of metal electrodes tends to decrease at higher temperatures, the sensitivity of state-of-the-art transducers decreases due to increasing electromechanical losses. Many oxide materials that withstand high temperatures and harsh atmospheres exist. Their typically low electrical conductivity excludes the use of thin-film oxide electrodes in transducers operating at near room temperature, whereas the thermally activated rise of electrical conductivity of oxides becomes beneficial at high temperatures of several hundred degrees Celcius (Schaumburg, 1994). Doping the materials can enhance this effect. For example, heavy strontium doping increases the conductivity of LGS significantly (Sauerwald et al., 2011; Bjørheim et al., 2014). Such films are expected to result in nearly epitaxial systems when deposited on the LGS substrates and, consequently, in stable devices. Other approaches dealing with e.g. lanthanum–strontium–magnesium-oxide (LSM) films (Lee et al., 2010) result in non-epitaxial electrodes and should not be pursued in this work.
1.2 Nearly monolithic langasite-based electrodes
A key for the successful combination of transducer material and oxide electrodes is that their conductivities significantly differ, with the electrode conductivity exceeding that of the transducer, i.e. the piezoelectric crystal, by several orders of magnitude. Keeping this in mind, an ideal solution would be to coat the transducer with an electrode exhibiting the same properties in terms of thermal and chemical expansion, reactivity, and lattice constants but with much higher conductivity. Either the film conductivity must be increased or the substrate conductivity must be decreased. Both situations are discussed subsequently.
As already mentioned above, LGS-type transducers are widely used. Here, strontium-doped LGS electrodes could fulfil the requirement of significantly increased conductivity according to the modelling of conductivity (Seh and Tuller, 2006). Based on these predictions, in Sauerwald et al. (2011) LGS resonators with Sr-doped electrodes are presented, which are obtained by thermal diffusion of Sr into the LGS single crystals. Although showing promising results, the disadvantage of this approach is its high complexity and time consumption because the diffusion of the dopant must be boosted by an electrical field at temperatures close to the melting point of LGS. For industrial applications, comparable electrodes prepared by a low-cost standard thin-film deposition technique would be desirable. Its realization is one aim of this work.
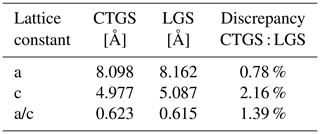
Compared to undoped LGS, the CTGS is less conductive (see Sect. 3.2.1). For this reason, a combination of doped LGS electrodes onto CTGS blanks as transducer material should improve the transducer performance. Strictly speaking, such a combination is not a monolithic system in this sense. However, CTGS and LGS are both quartz isomorphs belonging to the same crystallographic family (trigonal, symmetry class 32) and show only a minor difference in their lattice constants (see Table 1) (Bohm et al., 1999; Wang et al., 2003; Kugaenko et al., 2012). Therefore, the term “nearly monolithic” transducer is used.
1.3 Electrode orientation
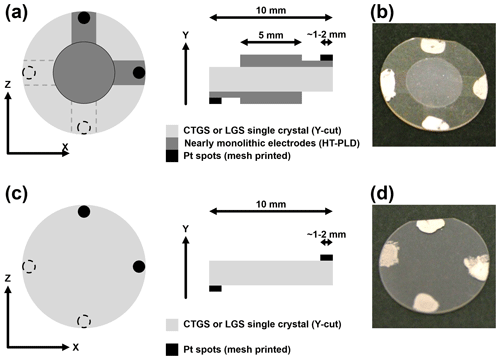
In general, the piezoelectric substrates used for BAW transducers are coated on both sides with keyhole-shaped electrodes. The contact stripes are aligned orthogonal to the direction of oscillation to reduce the influence on the resonator vibration. For CTGS and LGS the direction of the thickness-shear oscillation is along the crystallographic x axis (Ikeda, 1990; Ohsato, 2012). Consequently, the contact stripes of the keyhole-shaped electrodes are aligned along the z axis. The oxide electrodes are lightweight and stiffer with respect to platinum electrodes and should, therefore, impact the resonance behaviour less. This might result in different vibration properties. Therefore, the directional dependence of the influence of monolithic electrodes on the resonator performance is investigated in this work as well. To prove this hypothesis, CTGS resonators are coated with two sets of keyhole-shaped electrode pairs which are aligned along the x and z axis of the crystal (see Fig. 1a and b).
2.1 Piezoelectric transducers
The transducers used here are resonators consisting of stoichiometric LGS and CTGS plates coated with monolithic or nearly monolithic electrodes. The latter are grown by high-temperature pulsed laser deposition (HT-PLD) using the targets described in Sect. 2.3. The resonator blanks are Y-cut discs with a thickness of about 260 µm, purchased from SICCAS (China). Electroded Y-cut resonator blanks of the LGS family are generally excited in the thickness-shear mode (Ohsato, 2012). Besides the fundamental oscillation, higher harmonics can be stimulated as well. In this work the first, third and fifth harmonics of the resonators are characterized.
The substrate temperature during deposition is varied between 450 and 700 ∘C, and is varied from 10−3 to 10 Pa. For nearly monolithic resonators, the blanks are coated with keyhole-shaped electrodes (see Fig. 1). The thin-film electrodes are deposited using the L(3G)S_33Sr target at a substrate temperature of 450 ∘C and a of 0.02 Pa. As mentioned in Sect. 1.3, nearly monolithic resonators are coated with two orthogonal pairs of electrodes. The thickness of the films ranges from 1 to 3 µm.
Additional to the thin-film electrodes, the samples are coated at the edges with small platinum spots where the resonator makes contact with the measurement device. This contact pad is required to ensure the reliable electrical interface of the oxide electrodes or the resonator even at low temperatures, when the conductivity of the Sr-doped LGS electrodes is very low. These spots are applied with platinum paste (Ferro, USA) and subsequently fired at 1000 ∘C in ambient air (heating and cooling rate of 2 K min−1; holding time at 1000 ∘C of 1 h). To compare resonator blanks with electroded resonators, the former have only platinum spots without nearly monolithic electrodes atop, as shown in Fig. 1c and d.
2.2 Sample preparation for conductivity measurements
To determine the film conductivity, the 2.1 µm thick L(3G)S_33Sr films are deposited onto the whole surface of highly resistive sapphire substrates with a diameter of 10 mm (SITUS Technicals GmbH, Germany), and two 9 mm long platinum electrode stripes are mesh-printed over the film and fired at 1000 ∘C subsequently. The distance between the Pt stripes is 3 mm.
2.3 Target preparation for laser ablation
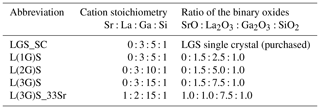
The targets used in this work are based on LGS stoichiometry. In order to compensate for gallium loss during the PLD, sputter targets with excess Ga content are prepared. Furthermore, strontium-doped targets are processed, in which Sr substitutes for La, to increase electrical conductivity. Table 2 correlates the abbreviations used in this work with the actual target stoichiometry.
The targets consist of the binary oxides La2O3 (purity: 99.99 %; Alfa Aesar, Germany), Ga2O3 (99.99 %; chemPUR, Germany), SiO2 (99.99 %; Merck, Germany) and SrO (99.95 Sr %; abcr, Germany) according to their molar ratio as given in Table 2.
As lanthanum oxide is hygroscopic, it tends to react with water vapour. Therefore, the as-purchased powders are potentially partially transformed to La(OH)3. To reverse this reaction, the purchased powders are annealed at 800 ∘C for at least 12 h to reverse the possible partial transformation to La(OH)3 before their mass is determined. An intermediate temperature step is added at 350 ∘C (holding time of 3 h) which is slightly above 330 ∘C, i.e. the temperature at which lanthanum hydroxide converts into lanthanum peroxide (La(OH)3 → LaOOH + H2O). Upon further heating, LaOOH decomposes to La2O3 (Brown and Gallagher, 1998). The X-ray diffraction before and after annealing confirmed the removal of water from the powders (diffraction patterns not shown here), showing no La(OH)3 reflections in thermally pre-treated powders directly after annealing. The La2O3 phase remains stable for several hours, which is sufficient for target production.
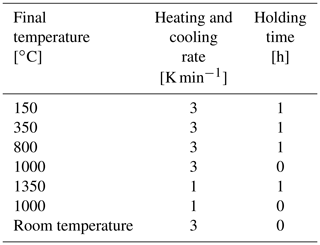
Appropriate masses of the binary oxide powders are mixed using a mortar and pestle. As only very small amounts of powder mixtures (typically 1.5–2 g) are processed at once, this simple approach is sufficient to obtain a homogenous intermix. Subsequently, the mixture is annealed at 150 ∘C for at least 12 h to reduce residual humidity. Thereafter, the warm powder is pressed into pellets (diameter of 13 mm; thickness of 2–3 mm) with a pressure of 13 MPa maintained for 1 min. Afterwards, the compacted pellets are sintered at 1350 ∘C in ambient air using the heating and cooling schedule as given in Table 3. The holding steps at 150, 350 and 800 ∘C may not be necessary. They are introduced as precautionary steps in case the pellets have absorbed water again or there is a slight decomposition of La2O3 to La(OH)3.
2.4 Thin-film deposition
The films are deposited by pulsed laser deposition using the targets listed in Table 2. The deposition chamber can be evacuated to a base pressure of 10−4 Pa. The reduction of the pump speed and simultaneous supply of oxygen by a solid electrolyte based pump (developed in the work group; Schulz et al., 2013) enable the use of atmospheres with controlled oxygen partial pressure () in the range from 10−4 Pa to several Pa.
The substrates are mounted on a high-temperature stable and insulating sample holder made of alumina and heated from the backside via a resistive heater tectra HTR01-01 (Germany), which is installed at the distance of less than 5 mm. The sample holder is rotating to improve the homogeneity of the films. The substrate temperatures are varied from room temperature (RT) to 700 ∘C.
The PLD system comprises a Lambda Physics COMPex 205 KrF excimer laser (Germany) with a wavelength of 248 nm and a pulse length of 25 ns. The typical deposition parameters are pulse energies of 200–250 mJ and repetition rates of 10–20 Hz. These deposition parameters result in film growth rates of 10–50 nm min−1 depending on , deposition temperature and target composition (Wulfmeier et al., 2019). The actual growth rate decreases with increasing temperature and increases with increasing . Total film thicknesses vary from several hundred nanometres to few micrometres and are specified below.
2.5 Film characterization
As-deposited films are inspected with a Euromex iScope optical microscope (the Netherlands). Film thickness and roughness are characterized with a tactile-surface Ambios XP-2 profilometer (USA), which is also used for the determination of the depth of craters resulting from secondary neutral mass spectroscopy (SNMS).
X-ray diffraction is performed to investigate the crystallinity of the films. Here, a Siemens D5005 (Germany) in Bragg–Brentano geometry is used. It is equipped with a Cu-Kα source and a scintillation detector. Measurements are performed at 30 kV and 30 mA. To suppress Kβ reflections an additional Ni shield is placed in the beam path in front of the detector.
Chemical composition of the deposited films is acquired by SNMS (Hiden Analytical, UK). The system includes an ion gun for Ar (purity 99.996 %) and a quadrupole mass spectrometer. The typical crater dimensions are 500×500 µm2. To suppress surface charging, a float gun is applied during the experiments. The ion counts of single-crystalline LGS substrates are used for the calibration of the system. The depth scale in the figure is calculated using the sputter time and the total depth of the sputter crater, assuming a constant sputter rate in the film and the substrate.
The film conductivity is determined by electrical impedance spectroscopy using a Solartron SI 1260 electrochemical interface (UK). High impedances at low temperatures are acquired using the SI 1260 in combination with a dielectric interface Solartron SI 1296 (UK). The latter extends the measurement range up to about 1015Ω. The film conductivity is calculated from the resistance R, extracted by fitting the parameters of a parallel circuit of resistor R and a constant-phase element to the high-frequency part, i.e. the first semi-circle, of the Nyquist plot. The samples are heated at a constant rate of 1 K min−1 in a DC-powered tube furnace GERO RO50-250-13SO (Germany). The temperature is determined a few millimetres away from the sample with a type S thermocouple connected to the Keithley DVM 2000 digital voltmeter (USA).
The resonance frequency is detected by a network analyser Agilent E5100A (USA). Here, the impedance spectra are recorded in the vicinity of the resonance frequency which is supported by automated frequency tracking (self-written software). Calibration of the system is done according to the three-term calibration scheme described in Haruta (2000). Temperature and heating and cooling are the same as for the determination of the film conductivity.
3.1 Homoepitaxial growth
3.1.1 Variation of the oxygen partial pressure
Figure 2 shows the Ga and La content of several samples deposited at different oxygen partial pressures (10−3 to 6 Pa) and substrate temperatures of 450 and 600 ∘C. The Si signal is not shown as it is not required for the further discussion. The solid grey lines represent the concentration in units of the molecular formula of LGS, i.e. undisturbed stoichiometry corresponding to y=5 and x=3. The calibrated SNMS yields, presented here, depend not only on the concentration of the elements but also on the matrix effect. Therefore, the calibration is only reliable close to concentrations of stoichiometric LGS single crystals, used as standards. These are purchased from three different manufacturers.
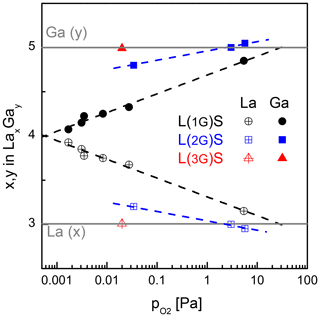
Figure 2Ga and La content determined by SNMS as function of the oxygen partial pressure during deposition. The count rate is calibrated by the use of the stoichiometric LGS single-crystalline substrates as standards. The films are grown at the substrate temperature of 600 ∘C (L(1G)S, (L(2G)S) and 450 ∘C (L(3G)S), respectively.
Thin films deposited from stoichiometric LGS targets at the lowest-achievable base pressure in the PLD system with a running substrate heater (equivalent to Pa) show a significant Ga deficit, which is a well-known effect for physical vapour deposition of many Ga-containing oxides (Brauer, 1975). The loss is mainly caused by the formation of volatile Ga suboxides in the vapour phase. The increase of the oxygen partial pressure during deposition reduces this deficit. However, even raising the to the technical limit of the deposition setup used in this work (i.e. Pa) does not result in a Ga:La ratio that is equivalent to the anticipated LGS stoichiometry. The extrapolation of the measurement data infers that of several tens of pascals are required for obtaining of stoichiometric films. Another disadvantage in using stoichiometric targets is the significantly decreased film deposition rate at high (Wulfmeier et al., 2019).
3.1.2 Variation of Ga content in the target
The second option to compensate the Ga deficit in the films is to use the off-stoichiometric targets, e.g. L(2G)S and L(3G)S. In this case, the general dependence of Ga and La content on the is the same as for L(1G)S. However, the related curves are shifted to higher Ga and lower La contents. For L(2G)S, stoichiometric Ga and La concentrations are achieved at –3 Pa and a substrate temperature of 650 ∘C. Figure 3 shows the comparison of SNMS measurements on films deposited from LGS_SC and L(2G)S targets on LGS single-crystal substrates. Here, depth profiles for all three cation species (La, Ga and Si) are presented. The Ga deficit is clearly visible in the film produced from the LGS_SC target without assisting the atmosphere. The film, deposited using the L(2G)S target and optimized conditions, shows a stoichiometry very close to LGS as can be seen from the nearly unchanged SNMS signals at the film–substrate interface. Not only is the stoichiometry correct for the latter film, but also a homoepitaxial growth is achieved under these deposition conditions, as seen in the X-ray diffraction patterns in Fig. 4. The pattern taken on the film (black curve) shows no reflexes other than (0y0) belonging to Y-cut LGS single crystals (grey curve). As the film thickness is about 1 µm, the contributions of the substrate to the detected X-ray diffraction (XRD) signal are nearly negligible. The growth of completely amorphous film is also unlikely, as this would result in significantly reduced intensity of the peaks at low angles and peak broadening for the given samples with films a few micrometres thick (Spieß et al., 2009). A more detailed discussion on this topic and on the growth of heteroepitaxial LGS thin films is published in Wulfmeier et al. (2019) and Zhao et al. (2017).
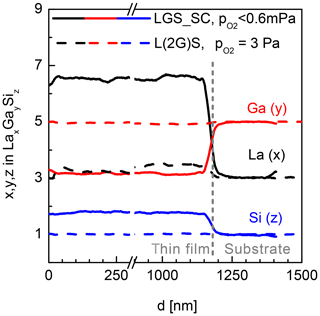
Figure 3Ga, La and Si content determined by SNMS in the LGS films. Comparison of a film deposited from LGS_SC target under the best-achievable vacuum, i.e. Pa (solid lines), and a film grown from the L(2G)S target at Pa (dashed lines). Deposition temperature is 600 ∘C for both films.
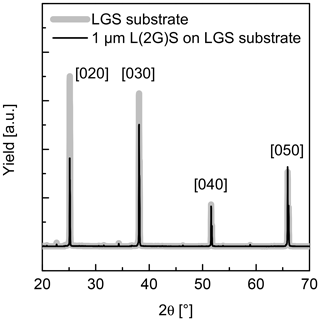
Figure 4XRD patterns of an LGS substrate before (grey curve) and after (black curve) film deposition using the L(2G)S target with deposition parameters of Pa and 600 ∘C. The film thickness of slightly more than 1 µm is sufficient to get a reliable XRD signal of the film. The yield is given in arbitrary units (a.u.).
Low deposition temperatures, low oxygen partial pressures and high growth rates are desired for industrial processes. In Wulfmeier et al. (2019) it is shown that the growth rate doubles if the substrate temperature is reduced from 700 to 450 ∘C for a given . To compensate for the increasing Ga loss at lower deposition temperatures, the gallium oxide content in the target has to be increased even more by changing the target composition from L(2G)S to L(3G)S. Simultaneously, the optimum has to be adjusted as well. Based on the experiences with the L(2G)S target and films, an initial parameter set of a lower substrate temperature of 450 ∘C and a of 0.02 Pa was chosen during deposition. The films deposited under these conditions show a stoichiometric cation content (red triangles in Fig. 2). As this first try already showed the anticipated stoichiometry, no further variation of the parameters has been made.
3.2 Strontium-doped LGS thin films
The target composition L(3G)S as well as deposition parameters of 450 ∘C and Pa, i.e. the parameter set resulting in stoichiometric LGS films, are chosen as a starting point for the preparation of Sr-doped LGS films. One third of lanthanum in the targets are replaced by strontium (target of L(3G)S_33Sr) in order to increase electrical conductivity. Figure 5 shows an X-ray diffraction pattern of a film grown on CTGS single crystal using the L(3G)S_33Sr target and deposition parameters stated above. This pattern is compared to diffraction patterns of uncoated CTGS and LGS single-crystalline substrates (Y-cut). The small shift between the (0y0) of LGS and CTGS is due to the slight difference of their lattice constants (see Table 1). The L(3G)_33Sr film shows the same reflections as the uncoated CTGS substrate, verifying an epitaxial film growth.
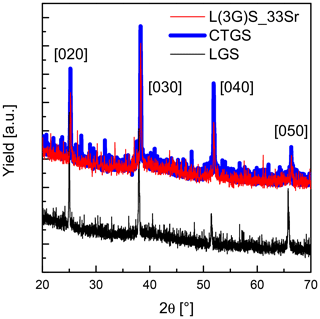
Figure 5XRD pattern of a film grown on a CTGS single crystal using the L(3G)S_33Sr target (red) and diffraction patterns of uncoated CTGS (blue) and LGS (black) single-crystalline substrates.
3.2.1 Thin-film conductivity
A film (thickness of 2.1 µm) is deposited using a L(3G)S_33Sr target on a sapphire substrate. Subsequently, it is characterized in the range from 600 to 1000 ∘C. Its conductivity σ rises in this range from 1.4 to 26.2 mS m−1 (see Fig. 6). The product of conductivity and temperature (σT) is about 1 order of magnitude higher than that of undoped LGS for a given temperature (blue curve). For comparison, the data for LGS single crystals purchased from the Leibniz Institute for Crystal Growth (Germany) are taken from Suhak et al. (2015). In Sauerwald et al. (2011) a highly doped monolithic resonator is demonstrated that is created by the thermal diffusion of Sr into the surface of the LGS single crystal. The diffusion depth is about 2.7 µm, which can be considered the equivalent thickness of an electrode. Here, the average Sr doping is 51 %, while within the first µm of the layer even 62 % of La cations are replaced by Sr. The conductivity of this surface layer (“LGS_62Sr”, red graph in Fig. 6) is several orders of magnitude higher than that of L(3G)S_33Sr. This behaviour is expected as in the former the Sr content is significantly higher than in this work. The increased conductivity of the Sr-doped LGS is consistent with the defect model presented in Seh and Tuller (2006).
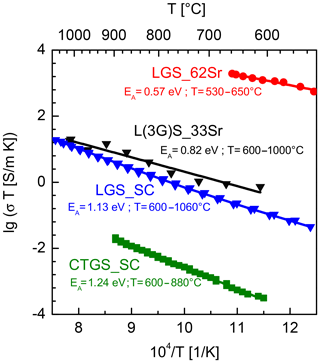
Figure 6Electrical conductivity of the Sr-doped thin film (prepared using the L(3G)S_33Sr target) compared to the bulk conductivity of CTGS and LGS single crystals (both data sets taken from Suhak et al., 2015) and to the conductivity of a highly Sr-doped LGS sample produced by Sr diffusion (LGS_62 Sr; data set taken from Sauerwald et al., 2011). The depiction of lg(σT) over the inverse temperature is chosen, since in the high-temperature range conductivity of LGS is governed by oxygen transport and comparability of the data should be ensured.
In addition, the product σTCTGS is determined using a CTGS single crystal purchased from FOMOS Materials (Russia). The corresponding conductivity data are taken from Suhak et al. (2015). The σTCTGS is about 3–4 orders of magnitude lower than σTL(3G)S_33Sr. Thus, the requirement of significantly higher conductivity of the electrodes (L(3G)S_33Sr thin film) is fulfilled with respect to CTGS single-crystal resonator blanks.
The activation energies of these conductivities are determined using an Arrhenius relation of the form
Here, σ0, k and T are a constant pre-exponential coefficient, the Boltzmann constant and the absolute temperature, respectively. At temperatures up to about 700 ∘C, the total conductivity of nominally undoped LGS is dominated by electronic conduction (Fritze, 2006). At higher temperatures, the ionic conduction prevails, and the pre-exponential factor of the corresponding Arrhenius expression becomes inversely proportional to T. The contribution of the ionic conductivity, i.e. the oxygen transport, to the total electrical conductivity is included in the following expression (Shewmon, 1963; Fritze, 2010):
Here, 2q, [OO] and D are the charge of the mobile species, the oxygen concentration and the oxygen diffusion coefficient, respectively. The activation energies EA obtained by fitting the data sets to the Arrhenius relation as well as the temperature ranges for fitting are depicted in Fig. 6. The activation energies of the Sr doped LGS samples are significantly lower than those of the LGS or even CTGS single crystals.
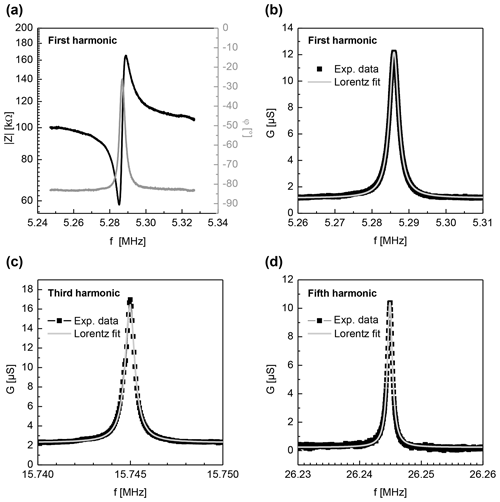
Figure 7Examples of impedance spectra of the nearly monolithic resonator excited via electrodes aligned along the x axis. All spectra are obtained at a temperature of 990 ∘C. Panel (a) shows the complex impedance (black curve on left axis) and the phase φ (grey curve on right axis) for first harmonic. Panel (b) shows the conductance G (experimental data, black dots) for the same data set and a corresponding Lorentz fit (grey curve), used for the calculation of the Q factor. Panels (c) and (d) are equivalent to (b), depicting the conductance of the for third and fifth harmonics, respectively.
Potentially, the samples are not fully equilibrated during these measurements as the data are obtained during constant heating or cooling. However, the very slow heating and cooling rates of about 1 K min−1 should only lead to small deviations from equilibrium.
3.2.2 Nearly monolithic resonator
Considering the application of LGS thin films for piezoelectric sensors, crystallinity and stoichiometry are important. For application as nearly monolithic oxide electrodes for piezoelectric resonators, the main focus regarding the doped LGS thin films is on the film conductivity which must be significantly higher than the resonator bulk conductivity. Here, a high current flow and, thus, a good electrical contact are achieved even for polycrystalline thin films. Sr-doped LGS films and CTGS single crystals fulfil this requirement.
The Y-cut CTGS resonator blanks are coated with two sets of electrodes, one aligned along the x axis of the crystals and one along their z axis. These samples are compared to resonator blanks without any electrodes. The resonance spectra are clearly visible for both sample configurations and both directions in the observed temperature range. For example, Fig. 7a depicts the complex impedance and the phase in the vicinity of the resonance frequency of a nearly monolithic resonator at 990 ∘C (electrodes in the x direction). These impedance spectra are similar to those detected on standard resonators with metallic electrodes. For the determination of the resonance frequency fR, the maximum of the conductance G is used as it is independent of stray capacities (Fritze, 2010). Spectra of G can be approximated by a Lorentzian function as depicted in Fig. 7b. Because of these features, such an approach is favoured also for the implementation in sensor devices, as it enables easy automatized fitting during the operation. The conductance peaks increase with temperature. This is expected as the oxide electrodes perform better at higher temperatures due to their increased conductivity and their low electrochemical losses (see Fig. 6).
The temperature-dependent resonance frequencies for all four sample configurations are depicted in Fig. 8. All dependences are normalized to the respective resonance frequency at 600 ∘C in order to visualize the nearly identical temperature dependence of frequency. This monotonous frequency decrease with temperature corresponds to the data of standard resonators with metal electrodes. However, there is an unexpected but significant difference between the CTGS resonators with oxide and metal electrodes. The frequency decrease with increasing temperature for CTGS resonators with metal electrodes is nearly linear. The temperature coefficient changes by only about 4 % in the range from 600 to 1000 ∘C (Suhak et al., 2016). In contrast, resonators with Sr-doped electrodes as well as the resonator blanks in this work show a significant curvature of the resonance frequency's temperature dependence (see Figs. 8 and 9). At the moment, there is no proved explanation for this behaviour which requires further work.
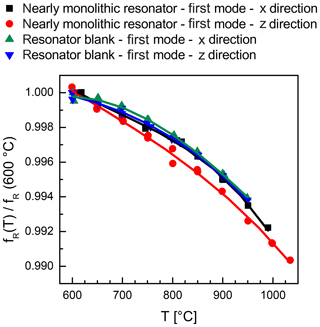
Figure 8A comparison of temperature dependence of resonance frequency for the nearly monolithic resonator and the resonator blank. Both are measured using electrodes aligned along the x as well as z axis. For comparability all data sets are normalized to the respective value of fR at 600 ∘C.
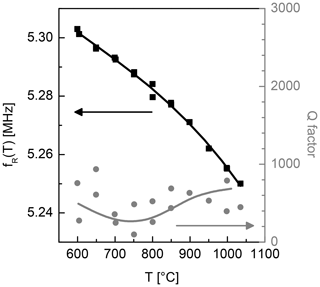
Figure 9Temperature dependence of the resonance frequency of the nearly monolithic resonator excited via electrodes along the z axis (left axis) and the corresponding Q factor (right axis).
The temperature dependence of resonant frequency is fully reproducible in the heating and cooling stages. Only the nearly monolithic resonator shows a slight deviation around 800 ∘C when measured in the z direction. Here, several overlapping peaks are visible in the impedance spectra over frequency, and the exact determination of the conductance maximum is very complicated in this small temperature region.
Figure 9 shows an example of the temperature dependence of resonance frequency and quality factor (Q factor) for the nearly monolithic resonator excited via electrodes along the z axis. Here, the absolute resonance frequency is depicted on the left axis. The right axis depicts the corresponding resonator quality factor (Q factor). The Q factor represents the electromechanical losses in the transducer and is calculated according to Fritze (2010). For the given samples, a slight increase of the Q factor with temperature is observed. In general, metal-electroded resonators show a decrease in this temperature region. In the present work, the increased Q factors are presumably due to higher stiffness of oxide electrodes with respect to metal electrodes. The Q factors for excitation along the x axis and the samples without electrodes are not depicted here. The average values of Q factors for the temperature region 800–1000 ∘C are summarized in Table 4. The results demonstrate the functionality of the nearly monolithic electrodes as they enhance the Q factor for both excitation directions. For metal electrodes, typically, the alignment in the z direction is preferred as it results in lower losses (see Sect. 1.3). In the present study, an alignment in the x direction leads to a higher Q factor. A similar behaviour is observed for free-standing LGS and CTGS resonators, too (Omelcenko et al., 2017).
Table 4Q factor of the nearly monolithic resonator and the resonator blank, both excited with electrodes aligned along the x and z axis. The data represent the average values in the high-temperature range of approximately 800 to 1000 ∘C.

In addition to the fundamental one, the third and the fifth harmonics are characterized. Their temperature dependent frequency is depicted in Fig. 10. They show the same slight curvature as observed for the first harmonic. Further, the curves are monotonous and deviations between heating and cooling are not observed, which indicates the reliability of the electrodes and stable transducer materials.
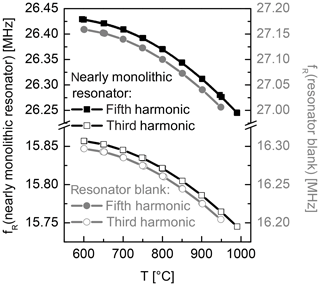
Figure 10Temperature dependence of the resonance frequency of the third and the fifth harmonics for the nearly monolithic resonator (black curves, left axis) and the resonator blank (grey curves, right axis).
Considering sensor applications, reliable frequency tracking is needed which, on the one hand, requires a high Q factor. On the other hand, the conductance peaks must not be affected by spurious modes. Furthermore, a reproducible and continuous temperature dependence of the resonance frequency is necessary, which is already demonstrated in Figs. 8–10.
Figure 7a shows the impedance spectra of the nearly monolithic resonator in the vicinity of the resonance frequency for the first harmonic. Figure 7b–d show the respective conductance spectra of the first, third and fifth harmonics and the Lorentz fits applied to these data sets. All of these spectra are recorded at about 1000 ∘C. Compared to metal electrodes, all these peaks show good signal quality, i.e. low damping or a high Q factor, and no spurious modes. In general, resonators with metal electrodes show even stronger damping for higher harmonics of vibrational modes. This is not observed for the oxide electrodes in this work. As the vibration profile shows stronger localization to the centre of the resonators (Benes et al., 1995; Edvardsson et al., 2006; Fritze, 2010; Schmidtchen et al., 2013) for vibrations of a higher order, the clear spectra for the third and fifth harmonics (even in the high-temperature region) favour the nearly monolithic resonators even more.
The epitaxial thin-film growth process presented in this work is optimized with respect to Ga content in the target for laser ablation, oxygen partial pressure and substrate temperature during deposition. Thus, epitaxial and dense LGS films are grown. They show monocrystallinity and stoichiometry equivalent to bulk LGS single crystals. Based on these results, Sr-doped LGS films are also grown, which show an increased electrical conductivity compared to undoped LGS in accordance with the defect model presented in Seh and Tuller (2006).
Even a further-increased difference in conductivities of electrode material and a transducer is achieved by deposition of the Sr-doped LGS films onto CTGS resonator blanks. Such oxide electrode films are proven to be stable at high temperatures. Thus, a nearly monolithic resonator is created. Its operation in the temperature range from 600 to 1000 ∘C is demonstrated. The temperature dependence of the resonance frequency is continuous and reproducible. The oxide electrodes increase the Q factor and show distinct resonance peaks, which are easy to fit with a Lorentzian function. This holds true not only for the first but also for the third and fifth harmonics. In contrast to resonators coated with metal electrodes, the sharp conductance peaks are observed even at very high temperatures of about 1000 ∘C.
So far, the developed oxide thin films show no noticeable degradation after several high-temperature runs. Hence, it is expected that such thin-film electrodes are stable in the long term. Thermal treatments up to 1000 ∘C for several days did not show any noticeable change in the surface morphology and resonance behaviour.
The data presented in this article are stored in an internal system according to the guidelines of the DFG. Research data are available upon request to the authors.
HW and RF are responsible for the sample preparation and characterization of the undoped films. LZ is a Master's student, who assisted in the experimental work. HW performed the experiments on doped layers, analyzed the data and wrote the initial paper. HF initiated the research project and supported HW and RF with the data interpretation and discussion. HF revised the paper and led the project. HW and HF approved the final paper.
The authors declare that they have no conflict of interest.
The authors gratefully acknowledge the financial support of the German Research Foundation (Deutsche Forschungsgemeinschaft; DFG) (grant no. FR 1301/20-1). In addition, the authors thank the Energy Research Centre of Lower Saxony (Energie-Forschungszentrum Niedersachsen; EFZN) for supporting this work.
This open-access publication was funded
by the Clausthal University of Technology.
This paper was edited by Robert Kirchner and reviewed by two anonymous referees.
Benes, E. Gröschl, M. Burger, W., and Schmid, M.: Sensors based on piezoelectric resonators, Sens. Act. A, 48, 1–21, https://doi.org/10.1016/0924-4247(95)00846-2, 1995.
Bjørheim, T. S., Haugsrud, R., and Norby, T.: Protons in acceptor doped langasite, La3Ga5SiO14, Solid State Ion., 264, 76–84, https://doi.org/10.1016/j.ssi.2014.05.017, 2014.
Bohm, J., Heimann, R. B., Hengst, M., Roewer, R., and Schindler, J.: Czochralski growth and characterization of piezoelectric single crystals with langasite structure: La3Ga5SiO14 (LGS), La3Ga5.5Nb0.5O14 (LGN), and La3Ga5.5Ta0.5O14 (LGT): Part I, J. Cryst. Grow., 204, 128–136, https://doi.org/10.1016/S0022-0248(99)00186-4, 1999.
Brauer, G.: Handbuch der Präparativen Anorganischen Chemie, 3rd Edn., Ferdinand Enke Verlag, Stuttgart, Germany, https://doi.org/10.1002/maco.19620131132, 1975.
Brown, M. E. and Gallagher, P. K.: Handbook of Thermal Analysis and Calorimetry, 1st Edn., Elsevier Science B.V., Amsterdam, the Netherlands, 1998.
Edvardsson, M., Rodahl, M., and Hook, F.: Investigation of binding event perturbations caused by elevated QCM-D oscillation amplitude, Analyst, 131, 822–828, https://doi.org/10.1039/b601800a, 2006.
Firebaugh, S. L., Jensen, K. F., and Schmidt, M. A.: Investigation of high-temperature degradation of platinum thin films with an in situ resistance measurement apparatus, J. Microelectromech. S., 7, 128–135, https://doi.org/10.1109/84.661395, 1998.
Fritze, H.: High-temperature bulk acoustic wave sensors, Meas. Sci. Technol., 22, 012002–012030, https://doi.org/10.1088/0957-0233/22/1/012002, 2010.
Fritze, H.: High temperature piezoelectric materials: Defect chemistry and electro-mechanical properties, J. Electroceram., 17, 625–630, https://doi.org/10.1007/s10832-006-9735-1, 2006.
Fritze, H., Schulz, M., Seh, H., and Tuller, H. L.: Sensor application-related defect chemistry and electromechanical properties of langasite, Solid State Ion., 177, 2313–2316, https://doi.org/10.1016/j.ssi.2006.02.008, 2006.
Gadkari, P. R., Warren, A. P., Todi, R. M., Petrova, R. V., and Coffey, K. R.: Comparison of the agglomeration behavior of thin metallic films on SiO2, J. Vac. Sci. Technol. A, 23, 1152, https://doi.org/10.1116/1.1861943, 2005.
Haruta, H.: Agilent technologies impedance measurement handbook, 2nd Edn., Agilent Technologies Co. Ltd, USA, 2000.
Ikeda, T.: Fundamentals of Piezoelectricity, 1st Edn., Oxford University Press, New York, USA, 1990.
Kreider, K. and Gillen, G.: High temperature materials for thin-film thermocouples on silicon wafers, Thin Solid Films, 376, 32–37, https://doi.org/10.1016/S0040-6090(00)01346-8, 2000.
Kugaenko, O. M., Uvarova, S. S., Krylov, S. A., Senatulin, B. R., Petrakov, V. S., Buzanov, O. A., Egorov, V. N., and Sakharov, S. A.: Basic thermophysical parameters of langasite (La3Ga5SiO14), langatate (La3Ta0.5Ga5.5O14), and catangasite (Ca3TaGa3Si2O14) single crystals in a temperature range of 25 to 1000 ∘C, Bull. Russ. Acad. Sci.: Phys., 76, 1258–1263, https://doi.org/10.3103/s1062873812110123, 2012.
Lee, S., Chu, C.-L., Tsai, M.-J., and Lee, J.: High temperature oxidation behavior of interconnect coated with LSCF and LSM for solid oxide fuel cell by screen printing, Appl. Surf. Sci., 256, 1817–1824, https://doi.org/10.1016/j.apsusc.2009.10.013, 2010.
Ohsato, H.: Origin of Piezoelectricity on Langasite, in: Materials Science and Technology, edited by: Hutagalung, S., IntechOpen, Rijeka, Croatia, 15–40, https://doi.org/10.5772/2223, 2012.
Omelcenko, A., Wulfmeier, H., Albrecht, D., El Mofid, W., Ivanov, S., Bund, A., and Fritze, H.: Thin-film calorimetry: In-situ characterization of materials for lithium-ion batteries, Int. J. Mater. Res., 108, 904–919, https://doi.org/10.3139/146.111551, 2017.
Richter, D., Sakharov, S., Forsén, E., Mayer, E., Reindl, L., and Fritze, H.: Thin Film Electrodes for High Temperature Surface Acoustic Wave Devices, Proced. Eng., 25, 168–171, https://doi.org/10.1016/j.proeng.2011.12.042, 2011.
Richter, D., Schulz, M., Sakharov, S., Davis, Z. J., and Fritze, H.: Surface Acoustic Wave Devices: Materials Stability in Harsh Environments, Mater. Res. Soc. Symp. Proc., 1519, mrsf12-1519-mm03-29, https://doi.org/10.1557/opl.2012.1716, 2013.
Sauerwald, J., Richter, D., Ansorge, E., Schmidt, B., and Fritze, H.: Langasite based miniaturized functional structures: Preparation, high-temperature properties and applications, Phys. Status Solidi A, 208, 390–403, https://doi.org/10.1002/pssa.201026639, 2011.
Schaumburg, H.: Keramik, 1st Edn., B. G. Teubner, Stuttgart, Germany, 1994.
Schmidtchen, S., Richter, D., and Fritze, H.: Variation of the vibration profile of piezoelectric resonant sensors with different electrode conductivity at high temperatures, Sens. Act. B, 187, 247–253, https://doi.org/10.1016/j.snb.2012.11.015, 2013.
Schröder, S., Fritze, H., Bishop, S., Chen, D., and Tuller, H. L.: Thin-film nano-thermogravimetry applied to praseodymium-cerium oxide films at high temperatures, Appl. Phys. Lett., 112, 213502, https://doi.org/10.1063/1.5025389, 2018.
Schulz, M. and Fritze, H.: Electromechanical properties of langasite resonators at elevated temperatures, J. Renew. Energ., 33, 336–341, https://doi.org/10.1016/j.renene.2007.05.016, 2008.
Schulz, M., Fritze, H., and Stenzel, C.: Measurement and control of oxygen partial pressure at elevated temperatures, Sens. Actuat. B, 187, 503–508, https://doi.org/10.1016/j.snb.2013.02.115, 2013.
Seh, H. and Tuller, H. L.: Defects and transport in langasite I: Acceptor-doped (La3Ga5SiO14), J. Electroceram., 16, 115–125, https://doi.org/10.1007/s10832-006-4081-x, 2006.
Seh, H., Tuller, H. L., and Fritze, H.: Defect properties of langasite and effects on BAW gas sensor performance at high temperatures, J. Eur. Ceram. Soc., 24, 1425–1429, https://doi.org/10.1016/S0955-2219(03)00464-3, 2004.
Shewmon, P. G.: Diffusion in Solids, McGraw-Hill, New York, USA, 1963.
Shimamura, K., Takeda, H., Kohno, T., and Fukuda, T.: Growth and characterization of lanthanum gallium silicate La3Ga5SiO14 single crystals for piezoelectric applications, J. Cryst. Grow., 163, 388–392, https://doi.org/10.1016/0022-0248(95)01002-5, 1996.
Spieß, L., Teichert, G., Schwarzer, R., Behnken, H., and Genzel, C.: Moderne Röntgenbeugung, 2nd Edn., Vieweg+Teubner, GMV Fachverlage GmbH, Wiesbaden, https://doi.org/10.1007/978-3-8349-9434-9, 2009.
Suhak, Y., Schulz, M., Richter, D., and Fritze, H.: High-Temperature Acoustical and Electrical Properties of LGS, LGT and CTGS Resonators, Sol. St. Phen., 230, 267–272, https://doi.org/10.4028/www.scientific.net/SSP.230.267, 2015.
Suhak, Y., Schulz, M., Wulfmeier, H., Johnson, W. L., Sotnikov, A., Schmidt, H., Ganschow, S., Klimm, D., and Fritze, H.: Langasite-Type Resonant Sensors for Harsh Environments, MRS Adv., 1, 1513–1518, https://doi.org/10.1557/adv.2016.109, 2016.
Thiele, J. A. and Pereira da Chunha, M.: High temperature LGS SAW gas sensor, Sens. Actuat. B, 113, 816–822, https://doi.org/10.1016/j.snb.2005.03.071, 2006.
Tuller, H. L. and Fritze, H.: U.S. Patent No. 6 370 955, 16 April 2002.
Wang, Z., Yuan, D., Cheng, Z., Duan, X., Sun, H., Shi, X., Wei, X., Lü, Y., Xu, D., Lü, M., and Pan, L.: Growth of a new ordered langasite structure compound Ca3TaGa3Si2O14 single crystal, J. Cryst. Grow., 253, 398–403, https://doi.org/10.1016/S0022-0248(03)01111-4, 2003.
Wulfmeier, H., Albrecht, D., Ivanov, S., Fischer, J., Ulrich, S., Bund, A., and Fritze, H.: High-temperature thin-film calorimetry: a newly developed method applied to lithium ion battery materials, J. Mater. Sci. 48, 6585–6596, https://doi.org/10.1007/s10853-013-7455-x, 2013.
Wulfmeier, H., Albrecht, D., Fischer, J., Ivanov, S., Bund, A., Ulrich, S., and Fritze, H.: Thin-Film Calorimetry: Analytical Tool for In-Situ Characterization of Lithium Ion Batteries, J. Electrochem. Soc., 162, A727–A736, https://doi.org/10.1149/2.0741504jes, 2015.
Wulfmeier, H., Omelcenko, A., Albrecht, D., Klimm, D., El Mofid, W., Strafela, M., Ulrich, S., Bund, A., and Fritze, H.: Thermal Stability of Materials for Thin-Film Electrochemical Cells Investigated by Thin-Film Calorimetry, MRS Adv., 1, 1043–1049, https://doi.org/10.1557/adv.2016.72, 2016.
Wulfmeier, H., Feder, R., Zhao, L., and Fritze, H.: Epitaxial Piezoelectric Langasite Thin Films for High-Temperature Application, MRS Adv., 4, 523–529, https://doi.org/10.1557/adv.2019.90, 2019.
Yu, F., Zhang, Sh., Zhao, X., Yuan, D., Qin, L., Wang, Q.-M., and Shrout, T. R.: Investigation of Ca3TaGa3Si2O14 piezoelectric crystals for high temperature sensors, J. Appl. Phys., 109, 114103, https://doi.org/10.1063/1.3592347, 2011.
Zhao, L., Feder, R., and Fritze, H.: Abscheidung von Langasit mittels Laserablation zur Herstellung hochtemperaturstabiler piezoelektrischer Sensorschichten, in: Proceedings 13. Dresdner Sensor-Symposium, Dresden, 188–193, https://doi.org/10.5162/13dss2017/P2.03, 2017.