Adjustment concept for compensating for stiffness and tilt sensitivity of a novel monolithic electromagnetic force compensation (EMFC) weighing cell

This paper describes the new adjustment concept of novel planar, monolithic, high-precision electromagnetic force compensation weighing cells. The concept allows the stiffness and the tilt sensitivity of the compliant mechanisms that are dependent on the nominal load on the weighing pan to be adjusted to an optimum. The new mechanism is set up and adjusted according to the developed mechanical model. For evaluation of the concept the system is tested on a high-precision tilt table and under high vacuum conditions in the environment of a commercially available mass comparator.

1 Introduction

In 2019 the système international d'unités (SI) was redefined by the use of fundamental physical and atomic constants (Stock et al., 2019). The definition of the kilogram by the international prototype kilogram (IPK) (Quinn, 1991) was replaced by the definition through the Plank constant h (BIPM, 2019). The revised SI ensures an invariable definition of the kilogram. Nevertheless, there are uncertainty issues.

Mass comparators are commonly used for the determination of mass. The counterweight principle allows many uncertainty sources to be shortcut and the resolution of the mass determination to be significantly increased. For example, a mass comparison at a specific site in a finite period of time is nearly independent of the well-known spatial variation in gravitational acceleration.

The main component of the highly sensitive devices is an electromagnetic force compensation (EMFC) weighing cell. They are essential for recent research concerning the new definition of the kilogram (Hilbrunner et al., 2018; Fröhlich et al., 2020; Rogge and Fröhlich, 2021). Nevertheless the sensitivity of the weighing cells S is dependent on mechanical stiffness C. A large contribution to uncertainties of the measurements with EMFC weighing cells is due to the weighing cell's sensitivity to tilt D. In the following, a concept to improve the performance of EMFC weighing cells based on mechanical adjustment is presented. The concept maximizes the sensor sensitivity from Eq. (1) by reducing the stiffness C→0, and at the same time, it minimizes the tilt sensitivity D→0, which results in a reduction of measurement uncertainties.

$$\begin{array}{}\text{(1)}& S=\mathrm{1}/C\end{array}$$

2 Operating principle of EMFC weighing cells

Monolithic EMFC weighing cells consist of a parallelogram guide structure realized by the upper (3) and the lower lever (2), connected to the base (1) by flexure hinges (A) and (B) and to the load carrier (4) by flexure hinges (C) and (D), as seen in Fig. 1. An upper weighing pan (6) and a lower weighing pan (5) are connected to the load carrier (4), for different applications. Usually only one of the weighing pans is used at the same time. The coupling element (7) connects the load carrier (4) with the transmission lever (8). The transmission lever (8) transmits the force of the counterweight ${\mathit{F}}_{\text{mC}}=m_{\mathrm{C}}\cdot \mathit{g}$ and the electromagnetic compensation force F_EMFC according to the lever ratio Γ from Eq. (2) of the point of force application $l_{{\mathrm{F}}_{\text{EMFC}}\mathrm{H}}$ and l_HG in the x direction to compensate for the forces ${\mathit{F}}_{\text{mS5}}=m_{\text{S5}}\cdot \mathit{g}$ or ${\mathit{F}}_{\text{mS6}}=m_{\text{S6}}\cdot \mathit{g}$. Similarly, deflections Δz are transmitted to the position sensor (PS).

$$\begin{array}{}\text{(2)}& \mathrm{\Gamma }={\displaystyle \frac{l_{F_{\text{EMFC}}\mathrm{H}}}{l_{\text{HG}}}}\approx \mathrm{4}\end{array}$$

The position sensor consists of an infrared-light-emitting diode and a differential photo diode, mounted face to face to the base, and a slit aperture mounted to the transmission lever. The components need to be fixed to the mechanism in its initial manufactured position, hereafter called the zero position. In the zero position, the differential photo diode and the infrared-light-emitting diode are adjusted in their position to the slit aperture at the lever until the differential voltage U_PS is zero. The differential voltage is obtained by transmitting the two photo currents from the differential photo diode by a transimpedance amplifier to a voltage signal. In this way the position of the lever can be detected by voltage measurements in further experiments.

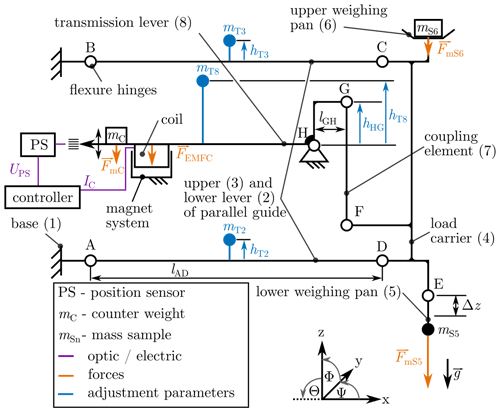
Figure 1 Operating principle of the prototype planar monolithic EMFC weighing cell with adjustment facilities (blue).

In a perfect, theoretical equilibrium state, the counterweight m_C counteracts the exact mass on one of the weighing pans (m_S5 or m_S6), and the weighing cell is in its zero position. In practical operation, the equilibrium state can only be reached by the application of an additional force F_EMFC from Eq. (3). It is a Lorentz force generated by a current carrying coil with a wire length of l in a magnetic field B. Assuming that the windings of the coil are orthogonal to the magnetic field (B⟂l), the coil current I_C is proportional to the generated Lorentz force (Eq. 3). With the detected deviation from the zero position by the position sensor, the coil current is driven by a PID controller to obtain the zero position.

$$\begin{array}{}\text{(3)}& F_{\text{EMFC}}=B\cdot l\cdot I_{\mathrm{C}}\end{array}$$

Since the mechanism shown in Fig. 1 is designed in a monolithic form, all joints (A–H) are flexure hinges. Each flexure hinge has a mechanical stiffness C_A–H due to its geometry, thickness and material properties (Weisbord and Paros, 1965). The total mechanical stiffness of the mechanism, with all flexure hinges, is further expressed as C_init from Eq. (4). It describes the correlation between a differential mass Δm on one of the weighing pans in addition to mass on the weighing pan (m_S5 or m_S6) and the resulting deflection Δz of the weighing pans. For further equations, it is assumed that g∥z axis from Fig. 1.

$$\begin{array}{}\text{(4)}& C_{\text{init.model}}=f\left(C_{\text{A-H}}\right)={\displaystyle \frac{\mathrm{\Delta }m\cdot g}{-\mathrm{\Delta }z}}\end{array}$$

The calculation of the initial stiffness of the mechanism C_init.FEM can be performed using finite element method (FEM) simulations or analytically C_init.model with good confidence in the nominal geometry (Torres Melgarejo et al., 2018; Henning and Zentner, 2021). Deviations from the measured stiffness of prototypes are prone to manufacturing uncertainties. Even small deviations of the thickness of the hinges in the range of micrometers are critical. One way to measure C_init is to control the weighing cell in its zero position. Once this is achieved, the coil current I_C is kept constant, the mass m_S6 is increased by Δm and the position Δz of the weighing pan is measured with an interferometer pointed at the weighing pan. With the mass difference Δm, the gravitational acceleration g and the deflection Δz, the stiffness can be calculated as presented in Eq. (4). The deflection at the weighing pan Δz, measured with the interferometer, is also used for the calibration of the differential voltage output of the position sensor. Once the calibration factor K_U has been determined (Eq. 5), small deflections can be measured by means of the position sensor. There is no further need for the interferometric measurement.

$$\begin{array}{}\text{(5)}& K_{\mathrm{U}}={\displaystyle \frac{\mathrm{\Delta }z}{\mathrm{\Delta }{U}_{\text{PS}}}}\end{array}$$

Similar to the determination of the calibration factor K_U for the representation of Δz at the weighing pan, a calibration factor for the current to force correlation K_I is determined. With the controller set point for the zero position, a calibration mass Δm is placed at the weighing pan, in addition to the mass samples (m_S5 or m_S6), while the coil current I_C is logged. The calculation of the calibration factor, representing the unknown parameters of the magnet system (B⋅l) and the approximate lever ratio (Γ), is presented in Eq. (6).

$$\begin{array}{}\text{(6)}& K_{\mathrm{I}}={\displaystyle \frac{B\cdot l}{\mathrm{\Gamma }}}={\displaystyle \frac{\mathrm{\Delta }m\cdot g}{\mathrm{\Delta }{I}_{\mathrm{C}}}}\end{array}$$

The set point of the controller can be above or below the zero position, measured with the position sensor. With the mass on the weighing pan (m_S5 or m_S6) kept constant while changing the set point of the controller, the stiffness can be calculated with the mass difference generated by the difference in the coil current ΔI_C, as described in Eq. (7).

$$\begin{array}{}\text{(7)}& \mathrm{\Delta }m={\displaystyle \frac{\mathrm{\Delta }{I}_{\mathrm{C}}\cdot B\cdot l}{g\cdot \mathrm{\Gamma }}}={\displaystyle \frac{\mathrm{\Delta }{I}_{\mathrm{C}}\cdot K_{\mathrm{I}}}{g}}\end{array}$$

A tilt of the base changes the direction of the force at the points of force application regarding the z axis and g. The tilt sensitivity D of EMFC weighing cells is the factor of influence by tilt to the measured mass deviation Δm_tilt. In the following, the tilt sensitivity is described as D_Θ for the tilt influences due to tilt around the y axis and D_Φ for the tilt sensitivity around the x axis (see Eqs. 8 and 9).

$$\begin{array}{}\text{(8)}& {\displaystyle }{D}_{\mathrm{\Theta }}={\displaystyle \frac{\mathrm{\Delta }{m}_{\text{tilt}}\cdot g}{\mathrm{\Delta }\mathrm{\Theta }}}\text{(9)}& {\displaystyle }{D}_{\mathrm{\Phi }}={\displaystyle \frac{\mathrm{\Delta }{m}_{\text{tilt}}\cdot g}{\mathrm{\Delta }\mathrm{\Phi }}}\end{array}$$

3 Adjustment concept

The adjustment of the EMFC weighing cell can go beyond the compensation of manufacturing and mounting deviations: it can be used to tune the mechanical properties of the weighing cell to highest sensitivity $S=\mathrm{1}/C$ while minimizing the tilt sensitivity D.

3.1 The auto-static state

This favorable adjustment state can be achieved by a combination of well-established adjustment methods for precision weighing systems: one method is the manipulation of trim masses m_Tn on bodies subject to rotary motion, e.g., the transmission lever of the weighing cell. The other measure is the introduction of a vertical distance h_HG between joint (H) and (G) (Darnieder et al., 2018). A perpendicular shift of a trim mass with respect to the gravitational acceleration vector g influences the static equilibrium of the balance, whereas the shift in direction of g alters stiffness and tilt sensitivity (Picard, 2004). With the stiffness, the period of free oscillations of the mechanical system is changing. In Conrady (1922), a value for the period of free oscillations was found experimentally, at which the balance is insensitive to tilt angles of its base relative to the g vector, the auto-static state. In this state, the tilt sensitivity is close to zero. Small tilts of the base, e.g., due to tidal movements of the earth's crust, do not affect the indication of the balance. Without further measures, the auto-static state of the weighing system corresponds to a certain period of free oscillations or stiffness. Consequently, the adjustment represents a trade-off between measuring sensitivity and tilt sensitivity, where the auto-static state is commonly sacrificed for a gain in measuring sensitivity (Picard, 2004).

For the typical EMFC weighing cells, this limitation can be overcome by the introduction of additional trim masses on the levers of the parallelogram guide (upper and lower lever in Fig. 1) (see also Darnieder et al., 2018, and Marangoni et al., 2017). The vertical positions of these trim masses with respect to the respective center of rotation are parametrized by h_T2 and h_T3. In combination with the trim mass on the transmission lever h_T8, the weighing cell can be adjusted to highest sensitivity (C≈0) while maintaining zero tilt sensitivity (D≈0; auto-static state). The auto-static state is now independent of the sensitivity of the weighing cell.

3.2 Reduction of initial stiffness C_init by h_HG

Even though theoretically possible, the compensation of the entire stiffness of the weighing cell mechanism by trim masses is impractical. Either large trim masses are required, or the adjustment measures become bulky. To compensate for the biggest part of the initial stiffness, a geometry change within the mechanism can be used. Here, the relevant parameter is denoted h_HG – the vertical distance between the effective rotational centers of joint (H) and joint (G). The effect on the stiffness is proportional to the force flow through the coupling element (7) (Darnieder et al., 2018). In other words, the mass on the weighing pan can effectively be used as a trim mass. This advantage is a disadvantage at the same time since the sensitivity of the weighing cell becomes load-dependent. However, this is not a limiting factor for the use in a mass comparator.

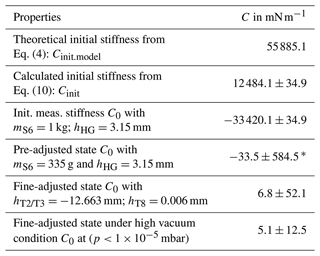
To reduce the measures and masses required for the adjustment, the initial stiffness C_init is compensated for by h_HG by manufacturing according to Eq. (10). The value for the initial stiffness was calculated according to Torres Melgarejo et al. (2018) and was estimated at C_init.model=55.9 N m⁻¹. To compensate for the initial stiffness, the adjustment parameter h_HG was chosen to be 3.15 mm, which is slightly less than the calculated value for h_HG(C₀=0), in order to avoid the possibility of a negative stiffness (inverted pendulum). The pre-adjusted stiffness C₀ should be close to zero but in a positive range. With h_HG=3.15 mm, the calculation according to Eq. (10) results in a stiffness of $C_{\mathrm{0},\text{calc.}}=\mathrm{6.35}$ N m⁻¹. The parameter m_G is the sum of all masses suspended at joint G.

$$\begin{array}{}\text{(10)}& C_{\mathrm{0}}=C_{\text{init}}+\left({\displaystyle \frac{h_{\text{HG}}^{\mathrm{2}}}{h_{\text{FG}}}}-h_{\text{HG}}\right)m_{\mathrm{G}}g{l}_{\text{HG}}^{-\mathrm{2}}\end{array}$$

3.3 Compensation of C₀ by fine-adjusting parameters

With the restriction of small rotations, applicable to EMFC weighing cells, the property variation due to an adjustment of the parameters h_T2, h_T3 (further summarized as h_T2/T3) and h_T8 can be described linearly as shown in Fig. 2. A deflection of the mechanism by Δz as well as a tilt of the base of the weighing cell will generate momentum by the trim masses m_Tn and the measures h_Tn. Depending on the sign of the measures h_Tn, introduced momentum M_Tn can compensate for the tilt sensitivity as well as the stiffness. The usage of a trim mass h_T8 on the transmission lever and the manufactured adjustment parameter h_HG is state-of-the-art. The introduction of the measures and trim masses on the parallel guide is new, more precisely at the upper (3) and lower lever (2). Technically, the trim masses and measures at the lower and the upper lever have the same effect, but for the assembly it is useful to use the lower lever if h_T2/T3<0 and the upper lever if h_T2/T3>0.

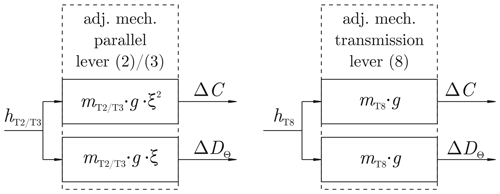
Figure 2 Linearized model equations for the adjustment of the properties stiffness C and tilt sensitivity D.

Ideally, one adjustment parameter is uniquely interrelated with one device property. As Fig. 2 shows, this is not the case. Every adjustment parameter changes both properties of interest (ΔC,ΔD). A mathematical model of the adjustment process enables a targeted adjustment. The linearized and simplified equations for both stiffness and tilt sensitivity yield $(\mathit{\zeta }=l_{\text{HG}}/l_{\text{AD}})$ (Darnieder et al., 2018)

$$\begin{array}{}\text{(11)}& {\displaystyle }C:\mathrm{0}=C_{\mathrm{0}}{l}_{\text{HG}}^{\mathrm{2}}-h_{\text{T8}}{m}_{\text{T8}}g-(h_{\text{T2}}{m}_{\text{T2}}+h_{\text{T3}}{m}_{\text{T3}})g{\mathit{\zeta }}^{\mathrm{2}}\text{(12)}& {\displaystyle }D:\mathrm{0}=D_{\mathrm{0}}{l}_{\text{HG}}+h_{\text{T8}}{m}_{\text{T8}}g+(h_{\text{T2}}{m}_{\text{T2}}+h_{\text{T3}}{m}_{\text{T3}})g\mathit{\zeta }.\end{array}$$

The values of the parameter C₀ and D₀ in Eqs. (11) and (12) need to be measured according to the measurement procedure described later in this paper with all adjustment parameters set to zero, except the manufactured h_HG. Given that every parameter is known except for the adjustment parameters, the equation system has one solution with m_T3=0. The required adjustment parameters can be estimated according to Eqs. (13) and (14):

$$\begin{array}{}\text{(13)}& {\displaystyle }{h}_{\text{T2/T3}}^{*}={\displaystyle \frac{l_{\text{HG}}(C_{\mathrm{0}}{l}_{\text{HG}}+D_{\mathrm{0}})}{g{m}_{\text{T2}}\mathit{\zeta }(\mathit{\zeta }-\mathrm{1})}}\text{(14)}& {\displaystyle }{h}_{\text{T8}}^{*}=-{\displaystyle \frac{l_{\text{HG}}(C_{\mathrm{0}}{l}_{\text{HG}}+D_{\mathrm{0}}\mathit{\zeta })}{g{m}_{\text{T8}}(\mathit{\zeta }-\mathrm{1})}}.\end{array}$$

Figure 3 Adjustment process for the EMFC weighing cell. The compliant weighing mechanism and the adjustment device are part of the weighing cell.

4 Measuring concept

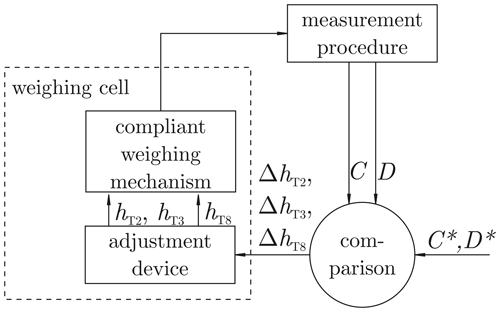
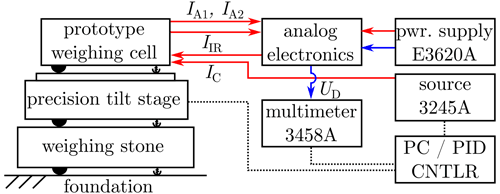
In order to realize the adjustment process described in Fig. 3, an automatized measurement routine is needed which delivers data about the stiffness and the tilt sensitivities. Therefore the weighing cell is placed on the high-precision tilt stage (Fig. 6), described in Rivero et al. (2014). It offers a tilt repeatability of less than 0.4 µrad in two axes (see also Yan et al., 2018, 2019). The control of the weighing cell is realized by a digital PID controller with programmable set point for the stiffness measurements. The analog electronics basically consist of a constant current supply for the infrared-light-emitting diode (I_IR) and a transimpedance amplifier to transform the photo currents (I_A1 and I_A2) of the differential photo diode to a voltage U_PS (also see Fig. 4). The voltage is measured by the multimeter Agilent 3458A, which forwards the information to the computer with the digital PID controller. With the differential voltage as input, the PID controller calculates the output in terms of the coil current (I_C) which is output by the power source Agilent 3245A, connected to the coil. The control cycle reaches a frequency of 20 Hz, which is sufficient for the inert mechanical system.

Figure 4 Schematic overview of the experimental setup with all peripheral units.

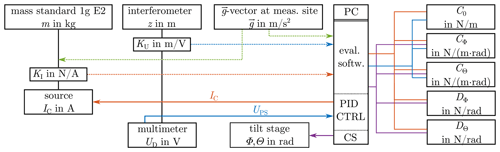
Figure 5 Information combination structure (CS – controller set point; PID CTRL – proportional integral derivative controller; PC – personal computer).

During the automatized measurement routine, the tilt stage tilts the base of the weighing cell according to predefined settings. For this procedure, 27 combinations of angles of $\mathrm{\Theta }=-\mathrm{15}\mathrm{\dots }+\mathrm{15}$ mrad and $\mathrm{\Phi }=-\mathrm{15}\mathrm{\dots }+\mathrm{15}$ mrad were predefined. In order to counteract drifts in the signal, the position $\mathrm{\Theta }=\mathrm{\Phi }=\mathrm{0}$ was set at the beginning (step 1), in the middle (step 13) and at the end (step 27) of each measurement routine. At each position, the offset current I_C and the stiffness were measured after a defined settling time. At the end of the measurement routine, a 3D data matrix can be processed and evaluated for the stiffness, for tilt sensitivities in each axis (D_Θ and D_Φ) and for tilt sensitivities of the stiffness itself (C_Θ and C_Φ). The obtained results can be retraced in the information combination structure in Fig. 5. The whole measurement routine has to be repeated after changing one of the adjustment parameters (m_Tn or h_Tn) or the weight on one of the weighing pans m_Sn, in order to investigate the influences and success of the adjustment.

5 Experimental investigations and results

For the experimental investigation, the weighing cell is set up on the precision tilt stage protected by an enclosure and a windshield to reduce the influence of air movement as shown in Fig. 6. A hood made from polystyrene covered the weighing cell during measurements to minimize the influence of temperature fluctuations. The measuring concept described above was used as the method to investigate the influences of the adjustment parameters (h_T2, h_T3, h_T8) in combination with the adjustment masses (m_T2, m_T3, m_T8) on the properties of the weighing cell concerning the stiffness and tilt sensitivities. The experiments were repeated for different loads (m_S6) on the weighing pan to gather information about the load dependency of the adjustment result. The momentum, M_Tn, described in Sect. 3, is an effective way to describe the combination of the adjustment parameters m_Tn with the adjustment measure h_Tn when divided by the gravitational acceleration, as described in Eq. (15):

$$\begin{array}{}\text{(15)}& {\displaystyle \frac{M_{\mathrm{T}n}}{g}}=m_{\mathrm{T}n}\cdot h_{\mathrm{T}n}\end{array}$$

Figure 6 Prototype weighing cell in enclosure on precision tilt stage.

For each load, tilt sensitivities and stiffness in dependence on the adjustment state were measured. For the expression of the adjustment success A_S, the results were combined by normalizing and adding the absolute values according to Eq. (16). Since we want to compensate for the stiffness as well as the tilt sensitivity to zero, the optimum point of adjustment is at A_S=0. The maximum values measured during the investigation of adjustment states with the same load of m_S6 were used for C_max and D_Θ,max. The tilt sensitivity orthogonal to the measurement direction (D_Φ) was not important for the adjustment success. It can not be influenced by the adjustment but delivers information about the parallelism of the axes of the tilt stage with the axes of the weighing cell.

$$\begin{array}{}\text{(16)}& A_{\mathrm{S}}=\left|{\displaystyle \frac{C_{\mathrm{0}}}{C_{\text{max}}}}\right|+\left|{\displaystyle \frac{D_{\mathrm{\Theta }}}{D_{\mathrm{\Theta },\text{max}}}}\right|\end{array}$$

Figure 7 Adjustment success for m_S6=1000 g.

Figure 8 Adjustment success for m_S6=334.829 g.

Figure 9 Adjustment success for m_S6=331.962 g.

Figure 10 Adjustment success for m_S6=275.109 g.

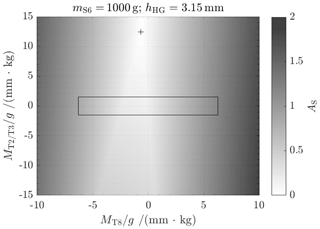
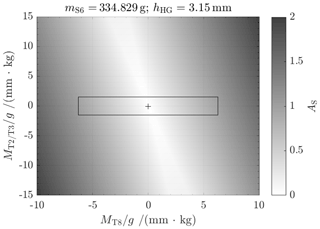
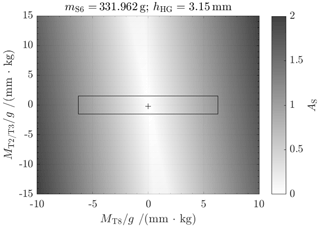
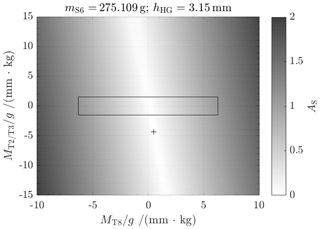
In Figs. 7–10, the results, in terms of adjustment success, from several measurement routines for each load (m_S6) are presented. The black cross shows the adjustment state for the actual load, calculated from the measurement results. The black rectangle represents the area of adjustability, limited by the installation space. All combinations inside of the rectangle allow for adjustment.

Originally, the load cell was designed with h_HG=3.15 mm for a stiffness slightly above zero. But after initial measurements with all adjustment parameters set to zero, the measured stiffness was $C_{\mathrm{0}}=-\mathrm{33.4}$ N m⁻¹ for m_S6=1 kg. The most likely reason for this is a deviation of thickness of the flexure hinges. The thin areas are difficult to manufacture, and deviations of only a few micrometers result in significant deviations (for more information on the calculation of stiffness of flexure hinges, see Torres Melgarejo et al., 2018). According to Fig. 7, the adjustment measures for h_T2/T3 could not be reached in this case. Nevertheless, in order to provide basic evidence for the correctness of the adjustment approach, the mass of the sample on the weighing pan was reduced to about 335 g (Fig. 8). For this, a stiffness close to zero and a tilt sensitivity in the range of adjustability are achieved. This state is further called the pre-adjusted state. Several measurements were performed with varying values for h_T8 and h_T2/T3, while the trim weights m_T8 and m_T2/T3 were kept constant. With the measurement results, the adjustment measures were calculated for the fine-adjusted state: $h_{\text{T2/T3}}=-\mathrm{12.663}$ mm and h_T8=0.006 mm.

Table 1 Adjustment success for stiffness.

Standard deviations k=1. ^* High standard deviation is caused by the instable condition of the weighing cell with negative stiffness (inverted pendulum).

Table 2 Adjustment success for tilt sensitivity.

Standard deviations k=1.

With the adjustment measures set to the weighing cell, the measurement procedure was repeated several times to obtain information about the repeatability. The results are presented in Tables 1 and 2 (fine-adjusted state). For the proof of vacuum compatibility, the measurements of the stiffness were repeated under high vacuum conditions ($p<\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ mbar) in the environment of a high vacuum mass comparator. The results of the repeated stiffness measurements under high vacuum conditions are presented in Table 1, and the results of the milestones during the adjustment procedure are presented in Tables 1 and 2.

6 Conclusions

A novel planar monolithic electromagnetic force compensation weighing cell was manufactured and investigated. The mechanical properties of the new weighing cell can be adjusted, which allows the stiffness and the tilt sensitivity to be compensated for in a more sophisticated way.

The verification of the adjustment approach was confirmed experimentally. The initially measured stiffness was compensated for to <1.1 ‰ in the pre-adjusted state and further reduced by $\mathrm{1}/\mathrm{5}$ in the fine adjusted state. The tilt sensitivity was compensated for to <1.3 ‰ compared to the initial measured tilt sensitivity or <2 % compared to the pre-adjusted state. The vacuum compatibility of the new mechanism was confirmed for further investigations in the environment of a vacuum mass comparator. Here, the performance of the system will be determined and compared to other systems. The knowledge about the manufacturing deviations in the weighing cell will be used for further investigation and the design of the next prototype. A further improvement can be achieved by the integration of an adjustment of the parameter h_HG in the mechanical structure. Thereby the influence of the load as trim mass itself can be counteracted, and the weighing cell can be adapted to a wide range of loads.