Determination of optimal crystallographic orientations for LiNbO₃ and LiTaO₃ bimorph actuators

The actuators for precise positioning based on bimorph structures of piezoelectric LiNbO₃ and LiTaO₃ crystals are considered. The optimal orientations of the actuator plates ensuring the highest possible displacements are determined by the extreme surfaces technique and the finite-element method. The simulated displacements for optimal orientations of LiNbO₃ and LiTaO₃ plates are compared with those obtained experimentally for manufactured LiNbO₃ and LiTaO₃ actuators, whose orientations are not optimal. As is shown, the optimal configuration of the actuator allows us to significantly increase its displacement for both LiNbO₃ and LiTaO₃ specimens.

1 Introduction

The systems for precise positioning are widely used to ensure high accuracy, linearity and reproducibility of the small movements of probes in scanning probe microscopes, micro-electromechanical systems, micro-dispensers, micro-motors for surgery, laser gyroscopes, mechanisms for laser resonator adjusting, piezo-drives for control systems of car suspensions and lamps, etc. (see, e.g., Segel, 2012; Uchino, 2017; Vijaya, 2017). To date, the most frequently used material for electromechanical actuators is the lead zirconate titanate-based piezo-ceramics (PbZr_xTi_1−xO₃, PZT). However, this material reveals two main fundamental properties which can limit its use. Firstly, the presence of lead in its composition prevents application of PZT in medicine. It is therefore necessary to note that in accordance with the regulations of the EU, lead-containing compounds are not allowed to be used in technical devices in the near future (Panda, 2009). Secondly, the low values of Curie temperature in PZT do not allow application of ceramic actuators at the temperatures higher than 300^∘. Therefore, searching for new lead-free materials operating at high temperatures is continuously performed. In this regard, piezoelectric ferroelectric crystals, particularly lithium niobate (LiNbO₃) and lithium tantalate (LiTaO₃), can be considered an alternative to PZT under certain operating conditions. More than 30 years of investigations have proven the use of LiNbO₃-based actuators (Nakamura et al., 1989, 1995; Ueda et al., 1990; Wakatsuki et al., 1998; Randles et al., 2006; Kawamata et al., 2007; Antipov et al., 2008; Matsunami et al., 2008; Bykov et al., 2014; Shur et al., 2015; Kubasov et al., 2016; Turutin et al., 2018; Buryy et al., 2019; Jiang et al., 2020), in particular in medicine (Randles et al., 2006). The active elements of LiNbO₃-based actuators could be manufactured in the form of bimorph crystalline plates (Nakamura et al., 1989, 1995; Ueda et al., 1990; Kawamata et al., 2007; Antipov et al., 2008; Bykov et al., 2014; Shur et al., 2015; Kubasov et al., 2016; Turutin et al., 2018; Buryy et al., 2019), multi-layer structures (Matsunami et al., 2008) and thin films (Jiang et al., 2020). These crystals possess many advantages compared to PZT, namely, higher Curie temperature, the virtual absence of hysteresis and creep, and weak dependences of the piezoelectric constants on temperature (Antipov et al., 2008; Shur et al., 2015). The main drawback of LiNbO₃ and LiTaO₃ compared to PZT is the lower value of piezoelectric constants by approximately an order of magnitude.

To increase the extent of deformation under the influence of the electric field, bimorph structures can be used. Such structures are formed by two bonded plates of piezoelectric crystals in such a way that the vectors of polarization (or its components) of both parts are anti-parallel and perpendicular to the bonding interface between them. In other words, such a configuration is a bidomain structure, which functions in accordance with the bimorph principle: applying a voltage leads simultaneously to the expansion of one layer and compression of the other layer; as the result, the element bends (Shur et al., 2015). Lithium niobate bimorph plates can be manufactured by a few techniques, i.e., by the thermo-chemical formation of the so-called inverse layer on a surface of a single-domain LiNbO₃ plate (Nakamura et al., 1989), by the electro-thermal method, particularly during infrared heating (Antipov et al., 2008; Bykov et al., 2014), and by direct bonding of high-quality polished and cleaned plates (Shur et al., 2015). We have manufactured such a bimorph structure using two lithium niobate plates bonded by means of diffusion, using copper from films deposited on the surfaces of the plates as a diffusant (Buryy et al., 2019). In this paper the orientations of connected crystalline plates were chosen in such a way that the perpendicular to the surfaces of the plates coincided with the z or (y+128^∘) directions. The chosen orientations were not optimal; however, it is known that in anisotropic crystals, including LiNbO₃, the phenomena of interaction of internal and external physical fields could be described by complex surfaces (see, e.g., Buryy et al., 2013). The developed methods of construction of such surfaces enable determination of optimal crystal cuts corresponding to the maxima of displacement.

It should also be noted that lithium tantalate crystals are isostructural and close in properties to LiNbO₃ and, therefore, could also potentially be used for production of actuators. However, to the best of our knowledge, there are no experimental or theoretical works where application of LiTaO₃ for actuator manufacturing was considered.

This work focuses on the determination of optimal spatial orientations of crystalline LiNbO₃ and LiTaO₃ plates for actuating applications to ensure the highest possible displacement of such actuators.

2 Optimization procedure

The considered design of the actuator is shown in Fig. 1. The unit vector m is parallel to the long edges of the bimorph (and perpendicular to the plane where the bimorph is fixed). The electric field E is applied along the short edges of the bimorph: $\mathit{E}=E\mathit{n}\perp \mathit{m}$, where E=|E|, n is the unit vector that determines the direction of the electric field.

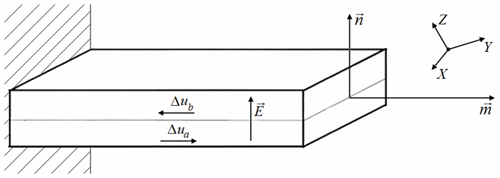
Figure 1 The bimorph actuator and the vectors that determine its geometry, directions of plate expansion/compression and the direction of the applied electric field.

Let us consider one plate of the bimorph separately. Under the influence of the electric field, its deformation can be described by tensor

$$\begin{array}{}\text{(1)}& \stackrel{\mathrm{̃}}{\mathit{\epsilon }}=\mathit{E}\stackrel{\mathrm{̃}}{d}=E\mathit{n}\stackrel{\mathrm{̃}}{d},\end{array}$$

where $\stackrel{\mathrm{̃}}{d}$ is the tensor of piezoelectric coefficients. The relative expansion of the plate along the vector m is equal to

$$\begin{array}{}\text{(2)}& \mathit{\delta }l={\displaystyle \frac{\left|\mathrm{\Delta }u\right|}{E{u}_{\mathrm{0}}}}=E^{-\mathrm{1}}\left|\mathit{m}\stackrel{\mathrm{̃}}{\mathit{\epsilon }}\mathit{m}\right|=\left|\mathit{m}\mathit{n}\stackrel{\mathrm{̃}}{d}\mathit{m}\right|,\end{array}$$

and, as is seen from Eq. (2), depends on the directions of m and n; here $\mathrm{\Delta }u=u_{\mathrm{0}}\mathit{m}\stackrel{\mathrm{̃}}{\mathit{\epsilon }}\mathit{m}$ is the absolute displacement of the plate, Δu>0 in case of plate expansion and Δu<0 in case of plate compression, and u₀ is the actuator length. Therefore the directions of m and n, which maximize the value of relative expansion δl, must be determined in order to optimize the actuator. Despite lithium niobate and lithium tantalate being crystals of sufficiently high symmetry (trigonal), here we intentionally solve the optimization problem in the most general formulation, while the same approach could also be used in future for low-symmetry crystalline materials, too.

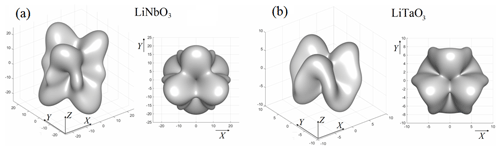
Figure 2 The extreme surfaces for LiNbO₃ (a) and LiTaO₃ (b) crystals (isometric and top views). All values on the axes are in pC $/$ N.

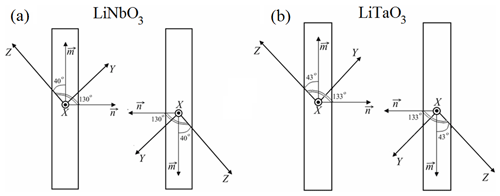
Figure 3 The optimal orientations of bimorph plates for LiNbO₃ (a) and LiTaO₃ (b); x, y, and z are the axes of the crystal-physics system of coordinates.

The optimization was performed using the approach developed for the analysis of induced and nonlinear optical effects in crystals (see, e.g., Buryy et al., 2013). This approach is based on the construction and analysis of the special-type (extreme) surfaces. Such surfaces comprise all possible maxima of the investigated effect which are achieved by determination of the optimal orientations of the determinant factor (electric field) n for all possible directions of crystal orientation determined by vector m. If the direction of n is defined by the angles θ_n, ϕ_n of the spherical coordinate system and the direction of m by the angles θ_m, ϕ_m, then δl (the objective function of the optimization) will depend on four variables θ_n, ϕ_n, θ_m, and ϕ_m. Now for each pair of angles θ_m, ϕ_m we can determine such angles θ_n max, ϕ_nmax which maximize the value of δl. Obviously, these angles depend on θ_m, ϕ_m, θ_n max ≡θ_n max(θ_m, ϕ_m), and ϕ_nmax=ϕ_n max(θ_m, ϕ_m), and δl can be considered a function of two variables θ_m and ϕ_m. The dependence δl_max(θ_m, ϕ_m) at θ_n=0 … π, ϕ_n=0 … 2π can be represented as a surface; the designation “δl_max” used here emphasizes that the dependence of δl_max is obtained after maximizing on θ_n, ϕ_n (parameters of the optimization). In accordance with the rule of determination of δl_max, we use the term “extreme” for such a surface. Thus the value of δl_max determines the length of the radius vector of this surface for the given direction of m. The angles θ_n, ϕ_n are varied during the optimization process in such a manner that the condition n⊥m is always fulfilled; i.e., the vector n rotates in the plane perpendicular to m. Subsequently, the piezoelectric extreme surface is given by

$$\begin{array}{}\text{(3)}& \mathit{\delta }{l}_{max}\left(\mathit{\theta },\mathit{\varphi }\right)=E^{-\mathrm{1}}\left|\mathit{m}{\mathit{n}}_{max}\stackrel{\mathrm{̃}}{d}\mathit{m}\right|,\end{array}$$

where n_max is the vector from a set of vectors n⊥m which maximize the value of δl for the fixed direction of m. The piezoelectric coefficients used in these calculations are indicated in Table 1. The extreme surfaces for both LiNbO₃ and LiTaO₃ crystals are shown in Fig. 2. As is mentioned above, each point of the surface represents the maximal value of the relative expansion δl_max for a given θ and ϕ, but the highest possible expansions correspond to the global maxima of the relative expansion, which, in their turn, correspond to the points which are the outermost from the origin of coordinates. The optimal directions of m and n as well as the corresponding values of δl_max are indicated in Table 1. It should be noted that alternatively the optimization can also be performed when the angles θ, ϕ coincide with θ_n, ϕ_n and the angles θ_m, ϕ_m are considered the variables. The obtained results for both optimization cases are the same; therefore, the latter case is not shown.

Figure 4 The deformation of the actuator under the applied voltage of 300 V (case i).

Table 1 The position and values of global maxima of the relative elongation δl_max for LiNbO₃ and LiTaO₃ crystals.

Only one set of the angles is given for each crystal. Other sets can be obtained using the symmetry elements of the $\stackrel{\mathrm{‾}}{\mathrm{3}}m$ point group (point group of crystals (3m) + center of inversion).

Table 2 The displacements of actuators (µm) under the excitation voltage of 300 V.

Since the maximal displacement of the actuator occurs when one plate maximally expands and the other one maximally compresses, the plates of the actuator have to be rotated relative to each other by 180^∘ in the YOZ plane. It is equivalent to application of the electric field of the opposite polarity to the plates. In this case the absolute values of the displacement will be exactly the same but with different signs. These optimal configurations of actuators are shown in Fig. 3. As is seen from the figure, they are almost similar for both LiNbO₃ and LiTaO₃: only the angles of rotation around the x axis show an insignificant difference (about 3^∘).

Figure 5 The dependencies of displacement on applied voltage for the actuators based on LiNbO₃ (a) and LiTaO₃ (b).

3 Simulation of bimorph actuators

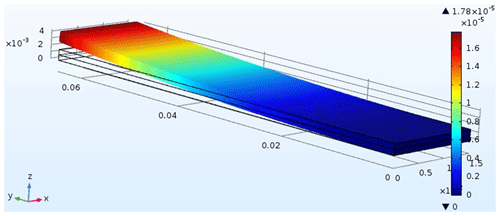
To determine the maximum extent of displacements of actuators, their simulation by the finite-element method was performed. In this simulation the geometry of actuators is similar to that used in our previous work (Buryy et al., 2019): width (x), length (y), and height (z) of each plate are 15, 65 and 0.75 mm, respectively; see Fig. 4 (dependence of actuator displacements on its geometry is analyzed in Buryy et al., 2019). The simulated excitation voltages are in the range from −300 to 300 V. Three different cases were considered: (i) the “initial” orientations of the plates – crystallographic z axes are perpendicular to the plates; (ii) the optimal orientations indicated in Table 1; (iii) y+127^∘ and y+36^∘ cuts for LiNbO₃ and LiTaO₃ correspondingly.

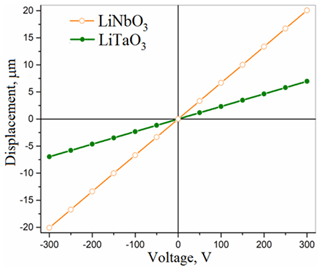
Figure 6 The dependencies of calculated displacement on applied voltage for the optimized actuators based on LiNbO₃ and LiTaO₃.

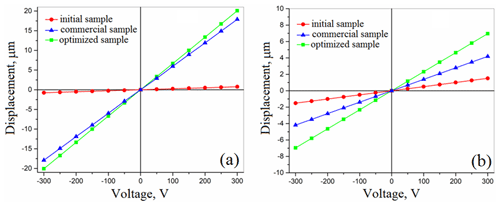
The cases for comparison were chosen for the following reasons. Case (i) corresponds to the orientation of the already manufactured LiNbO₃-based actuator (Buryy et al., 2019). Moreover, in this paper the dependencies of actuator displacements are theoretically analyzed with variations of actuator length (from 10 to 80 mm) and thickness (from 0.4 to 2.4 mm). Since the main peculiarities of these dependencies were revealed in Buryy et al. (2019), we do not repeat the same analysis here. Case (ii) corresponds to the optimal orientations determined in the current study (see Table 1). Case (iii) corresponds to the commercially available cuts of LiNbO₃ and LiTaO₃ characterized by the highest values of transversal piezoelectric coefficients (Matsunami et al., 2008; Kubasov et al., 2016).

The results of the simulation, i.e., the absolute values of displacements of bimorph plates, are shown in Figs. 5–6 and indicated in Table 2. As well as in Buryy et al. (2019), the dependencies of actuator displacement on excitation voltage are linear in all the studied voltage ranges, i.e., up to a field strength of 200 V/mm. As is shown, the optimal configuration of the actuator allows us to sufficiently increase the displacement value (with other parameters fixed): the displacement is 26 times higher for lithium niobate and 4.6 times higher for lithium tantalate compared to the actuator, studied in Buryy et al. (2019) (case (i)). Compared to the commercially available plates (case (iii)), the displacement increases for about 11 % for LiNbO₃ and 67 % for LiTaO₃.

The displacement of the LiNbO₃ actuators with optimized orientation is about 3 times higher compared to that of LiTaO₃; see Fig. 6. However, the displacement of the LiTaO₃ actuator is 2 times higher when case (ii) is considered. So, in case the use of z-cut plates is desired from the technological point of view, the application LiTaO₃ is preferable.

The obtained simulation results will be used for preparation of bimorph actuators with optimal orientations in the forthcoming research.

4 Conclusions

The actuators for precise positioning based on bimorph structure formed by joining lithium niobate and lithium tantalate plates of different crystallographic orientations are considered. To ensure the highest possible displacements of the actuator, the optimal orientations of their plates were determined by the extreme surfaces technique. The possible absolute values of displacements are determined by simulation using the finite-element method. It is shown that the optimal orientations of the long edges of the actuator plates are defined by the angles θ_m=40^∘, ϕ_m=90^∘ for LiNbO₃ crystal and by θ_m=43^∘, ϕ_m=90^∘ for LiTaO₃. The electric field is applied in the directions determined by the angles θ_n=130^∘, ϕ_n=90^∘ and θ_n=133^∘, ϕ_n=90^∘ for LiNbO₃ and LiTaO₃, respectively. The optimal configuration of the actuator allows us to sufficiently increase its displacement (with other parameters fixed): in 26 times for LiNbO₃ and in 4.6 times for LiTaO₃ compared to the previously manufactured actuator with the z axes of the plates perpendicular to the surface of bonding. In comparison with the commercially available LiNbO₃ y+127^∘ cut and LiTaO₃ y+36^∘ cut, the displacement increases for about 11 % for LiNbO₃ and 67 % for LiTaO₃. For the optimized design, the displacement of the LiNbO₃ actuator is about 3 times higher than that of LiTaO₃. However, for the case when the z axes of the plates are perpendicular to the bonding surface, the displacement is twice as high for the LiTaO₃ actuator compared to LiNbO₃.